| 这个作业属于哪个课程 | https://edu.cnblogs.com/campus/zswxy/software-engineering-2017-1 |
| 这个作业要求在哪里 | https://edu.cnblogs.com/campus/zswxy/software-engineering-2017-1/homework/10494 |
| 这个作业的目标 | 实现一个命令行程序,不妨称之为Sudoku。 |
| 作业正文 | 此文章 |
| 其他参考文献 |
www.baidu.com,知乎 |
1、Github项目地址
https://github.com/hangoveri1/20177666
2、PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 20 | 30 |
| Estimate | 估计这个任务需要多少时间 | 20 | 20 |
| Development | 开发 | 800 | 1200 |
| Analysis | 需求分析 (包括学习新技术) | 20 | 30 |
| Design Spec | 生成设计文档 | 90 | 90 |
| Design Review | 设计复审 | 25 | 25 |
| Coding Standard | 代码规范 (为目前的开发制定合适的规范) | 0 | 0 |
| Design | 具体设计 | 60 | 90 |
| Coding | 具体编码 | 600 | 950 |
| Code Review | 代码复审 | 20 | 25 |
| Test | 测试(自我测试,修改代码,提交修改) | 120 | 150 |
| Reporting | 报告 | 120 | 360 |
| Test Repor | 测试报告 | 40 | 60 |
| Size Measurement | 计算工作量 | 0 | 0 |
| Postmortem & Process Improvement Plan | 事后总结, 并提出过程改进计划 | 90 | 120 |
| 合计 | 2005 | 3150 |
3、解题思路
3.1问题描述
实现一个命令行程序,不妨称之为Sudoku。
数独盘面是个九宫,每一宫又分为九个小格。在这八十一格中给出一定的已知数字和解题条件,利用逻辑和推理,在其他的空格上填入1-9的数字。使1-9每个数字在每一行、每一列和每一宫中都只出现一次,所以又称“九宫格”。
具体任务:
现在我们想一步一步来,完成从三宫格到九宫格的进阶;完成三宫格和其他博客任务,就算过了初级考核,其他的算升级。具体各阶规则如下:
三宫格:盘面是3*3。使1-3每个数字在每一行、每一列中都只出现一次,不考虑宫;
四宫格:盘面是2*2四个宫,每一宫又分为2*2四个小格。使1-4每个数字在每一行、每一列和每一宫中都只出现一次;
五宫格:盘面是5*5。使1-5每个数字在每一行、每一列中都只出现一次,不考虑宫;
六宫格:盘面是2*3六个宫,每一宫又分为3*2六个小格。使1-6每个数字在每一行、每一列和每一宫中都只出现一次;
七宫格:盘面是7*7。使1-7每个数字在每一行、每一列中都只出现一次,不考虑宫;
八宫格:盘面是4*2八个宫,每一宫又分为2*4八个小格。使1-8每个数字在每一行、每一列和每一宫中都只出现一次;
九宫格:盘面是3*3九个宫,每一宫又分为3*3九个小格。使1-9每个数字在每一行、每一列和每一宫中都只出现一次;

3.2理解问题
该算法题的需求是实现一个称之为Sudoku命令行程序。
程序要实现利用逻辑和推理,在在数独盘面的空格上填入1-9的数字。使1-9每个数字在每一行、每一列和每一宫中都只出现一次。
输入要求输入文件名以命令行参数传入。
输出要求输出n个程序解出的盘面,每两个盘面间空一行,每个盘面中,每两个小格之间有一个空格。
3.3思考如何实现
数独是需要我们去按规则填写数字:同一行同一列不能出现相同数字,非素数阶数还需要满足每个宫内不能有相同数字。
我查阅了很多资料思考用什么方法去实现,
第一种想法 —— 蛮力法
第二种想法 —— DFS
第三种想法 —— 回溯法
回溯法思想
在包含问题的所有解的解空间树中,按照深度优先搜索的策略,从根结点出发深度探索解空间树。当探索到某一结点时,要先判断该结点是否包含问题的解,如果包含,就从该结点出发继续探索下去,如果该结点不包含问题的解,则逐层向其祖先结点回溯。(其实回溯法就是对隐式图的深度优先搜索算法)。 若用回溯法求问题的所有解时,要回溯到根,且根结点的所有可行的子树都要已被搜索遍才结束。 而若使用回溯法求任一个解时,只要搜索到问题的一个解就可以结束。
这些算法我都不怎么了解,然后我决定先去了解分析了数独的填数字规则和要求,在了解了题目的规则以后,我觉得回溯法非常的适合,因为对于生成的数独终局,我们只要按顺序一个一个填数字就好啦,每完成一个数字都检查它的所在行,列和宫是否满足数独规则,若满足就填写下一个数字,否则则回溯,之后就在编写代码的路途上一去不复返了……

4、设计实现过程
4.1函数模块的设计
- 根据本题的解题要求和思考中确定的递归解题思想,应设计以下模块:
- 主函数模块(数值的输入,合法性判断,试值的判断,试值的检查)
- 输出文件生成模块
4.2具体功能函数设计
-
main()函数
- 接受命令行参数,并进行解析
- 读取输入的数字矩阵,对当前坐标格子状态和递归状态进行判断(flag的值)
- 根据矩阵数量尝试填入数值,并且用循环语句进行判断是否填入该数值
- 验证失败的话就回溯继续填入数值进行判断
-
output函数
- 对于main函数中的试值判断结果进行输出显示出来
-
check函数
- 对传入的坐标进行行列和宫进行重复判断和定位
- 根据是否合法返回布尔值
-
vfprintf函数
- 根据传入的矩阵数值将该矩阵写入output函数中
-
简单流程图
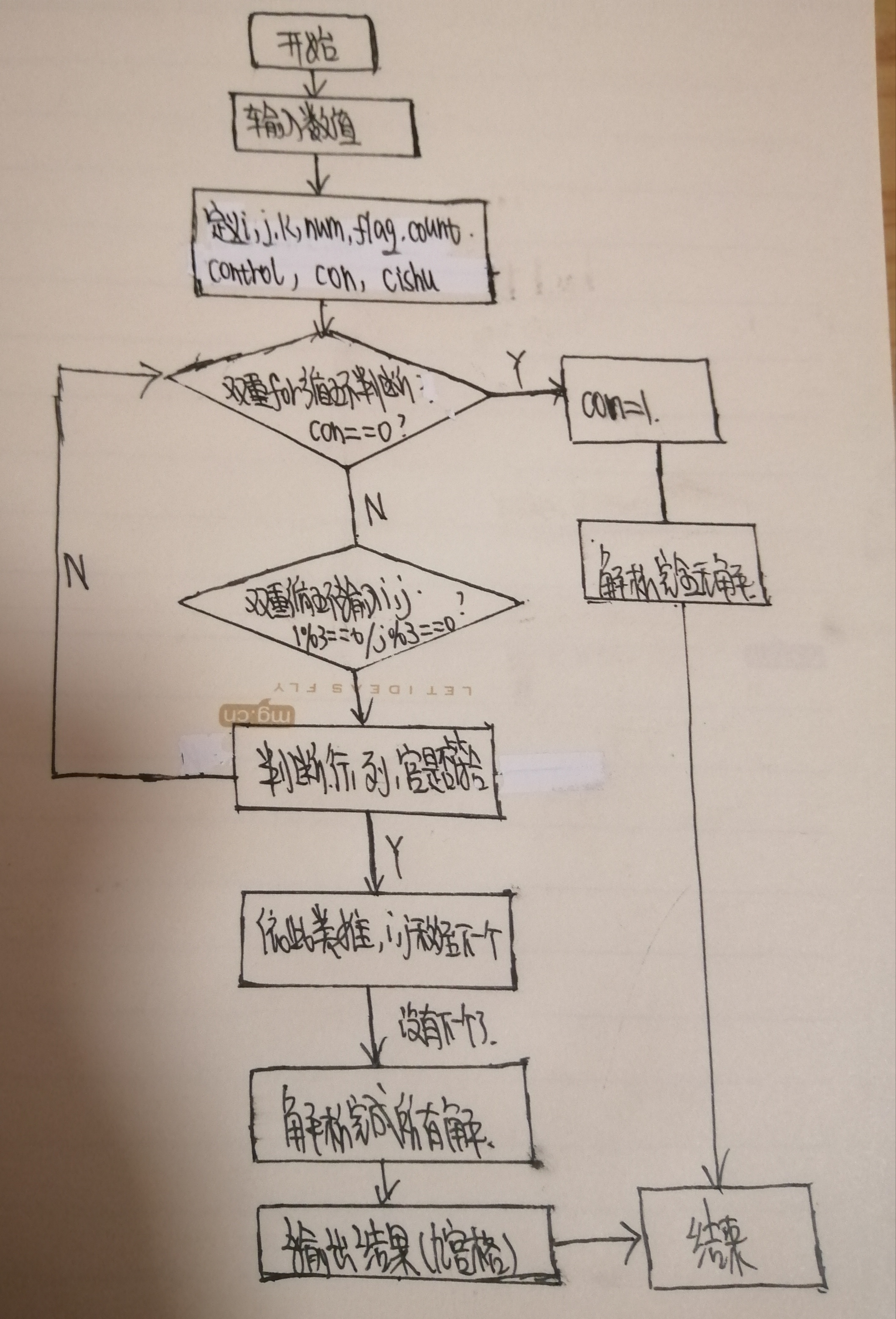
4.3变量设置
- int str[9][9]
- int i,j,k,num,flag,count,control,con,cishu
5、改进思路
5.1代码静态分析
我写了两个代码,这是第一个代码的静态检查出现的问题,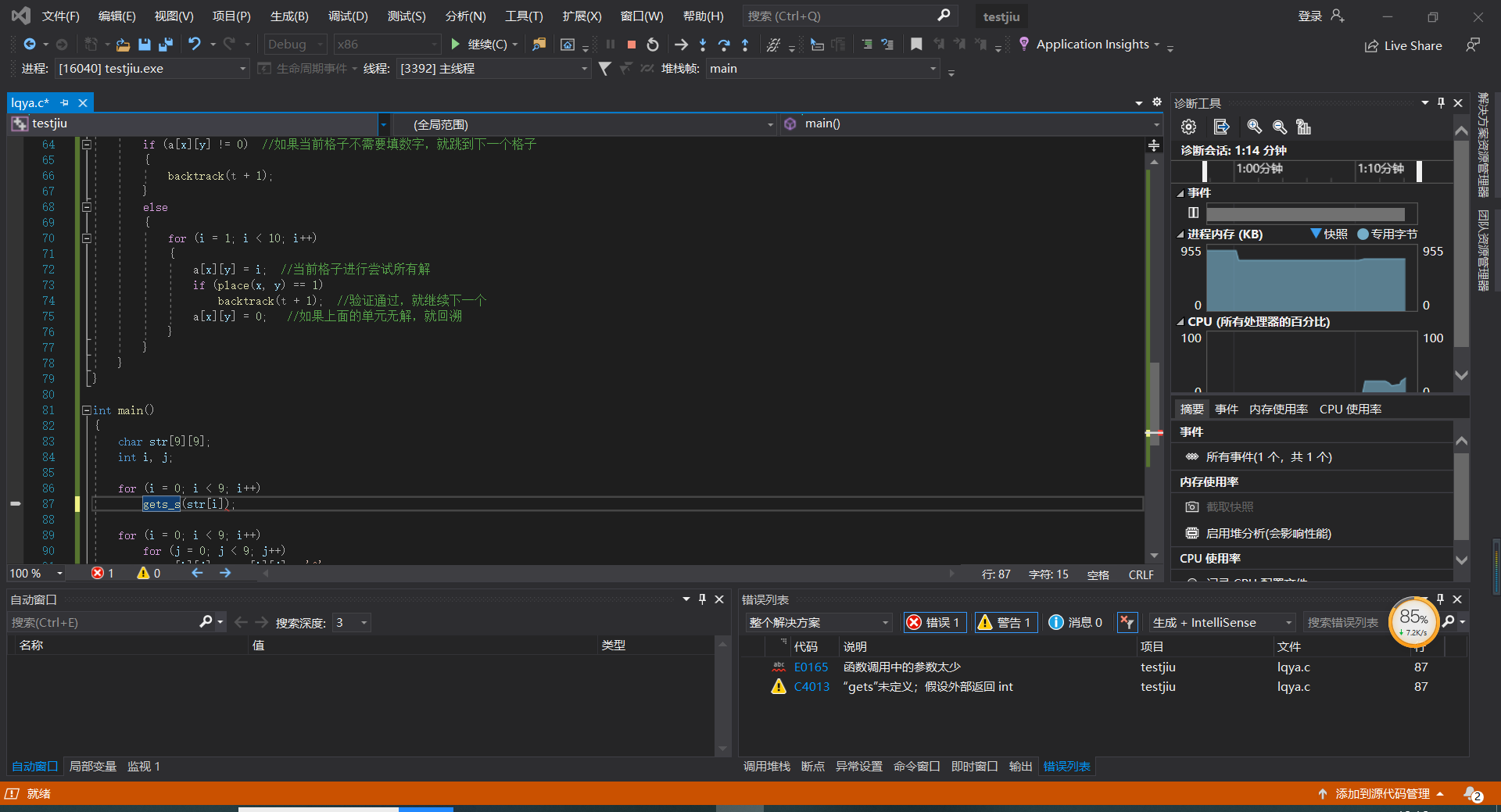
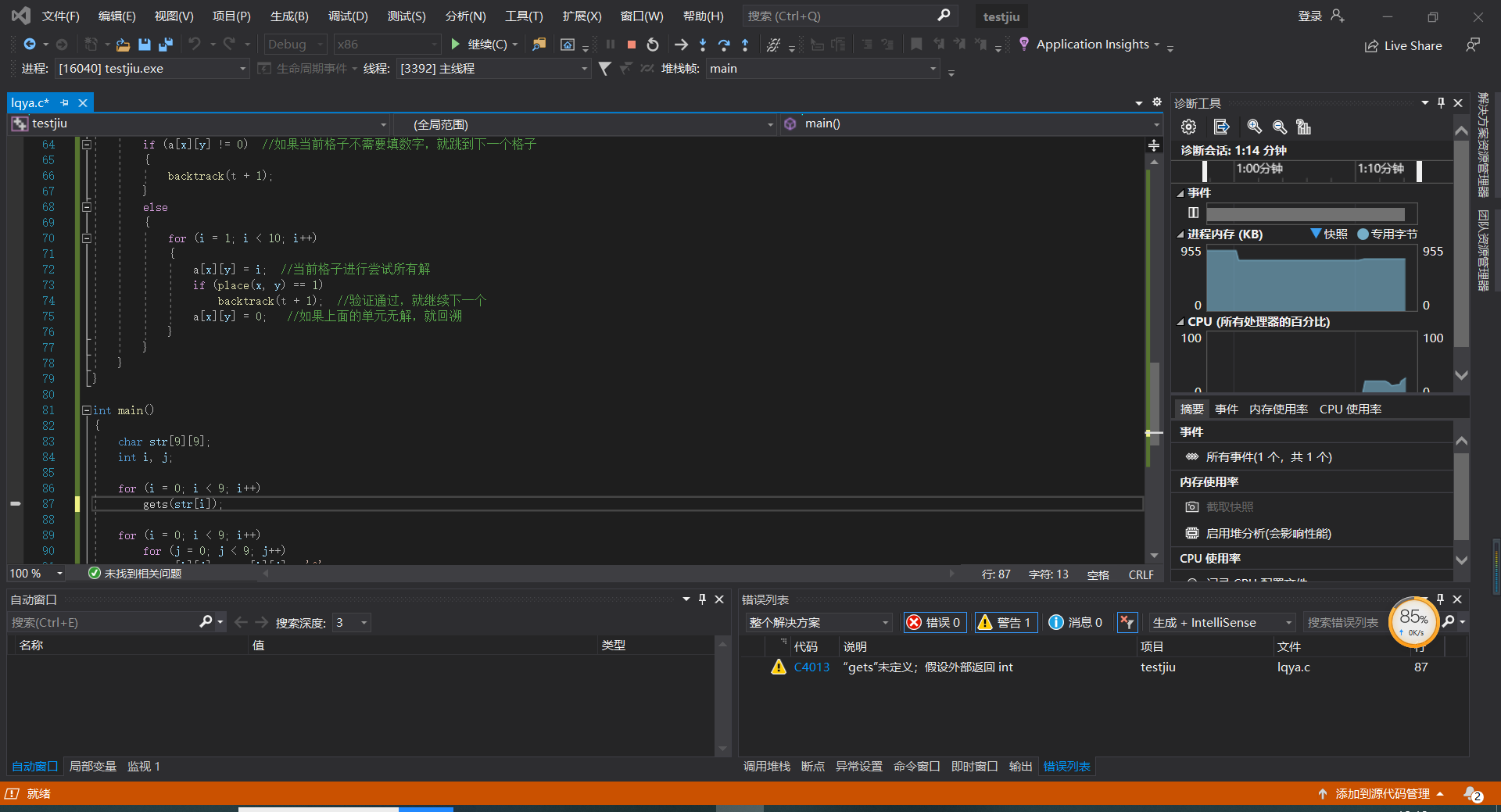
加以改进后还是有问题,我反复查阅资料虽然解决了,但是分析却分析不出来了,我就试一试另外一种方法进行改写,(害,真的太烦人啦)

5.2代码性能优化
这个main函数里面的东西占CPU时间很多,执行单个工作最多的函数_stdio common _vfprintf独占时间百分比居然有79.57%,而且它只调用了一次就占这么多时间,反观调用次数最多的_checkForDebugge...被调用九次也没占多少时间,所以我应该吧把main方法中的那个循环语句,也就是判断数值的行列写得更加简单些,然后我就开启了很长一段时间的改写,最终结果就是无法进行性能分析……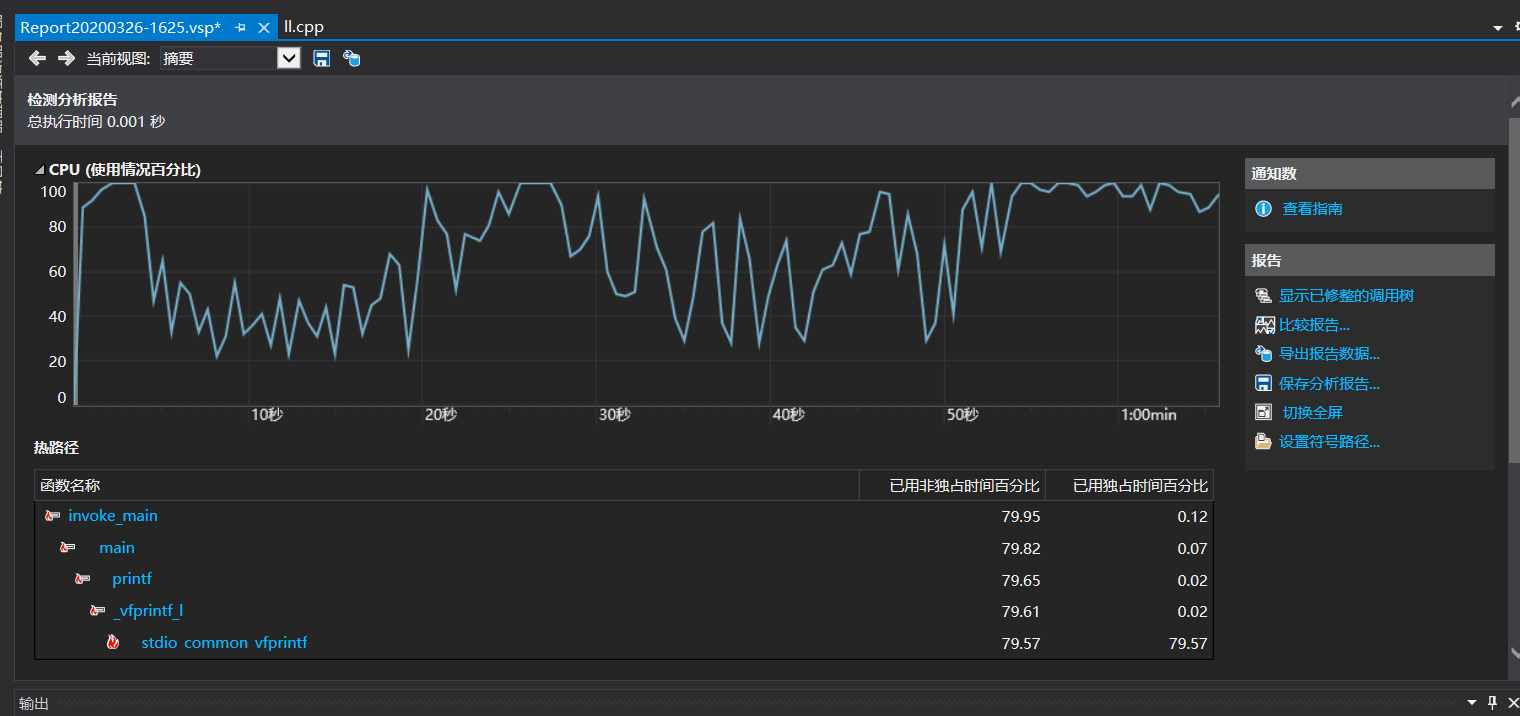
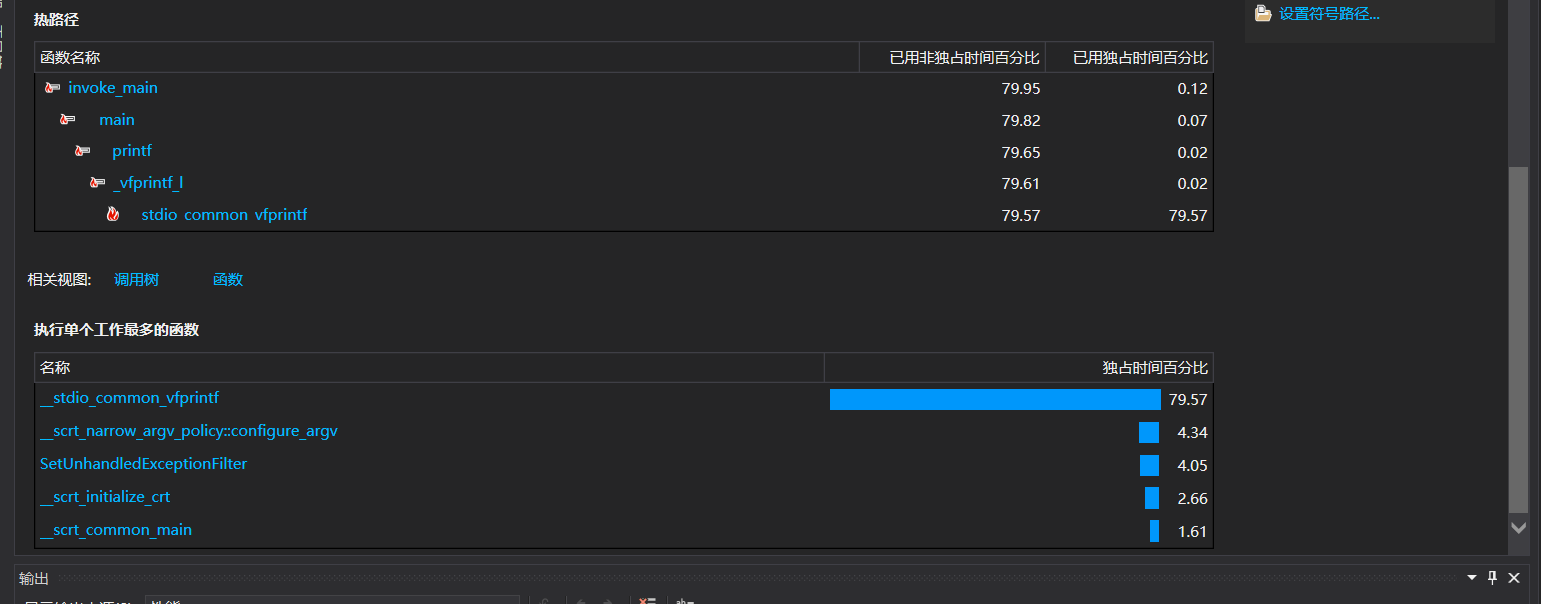
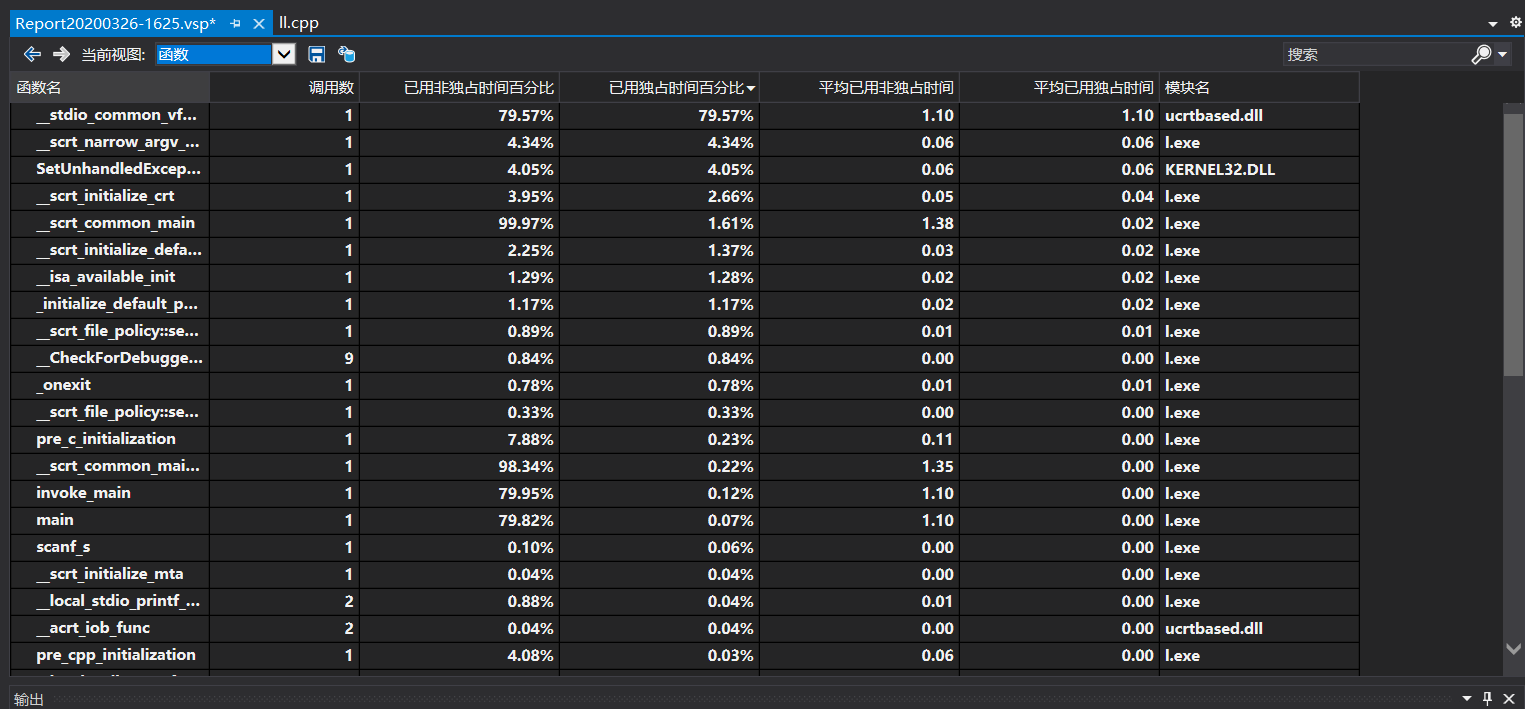


5.3单元测试
软件有问题,单元测试不出来……唉

6、代码的运行出现的错误以及更改(简单描述几个)
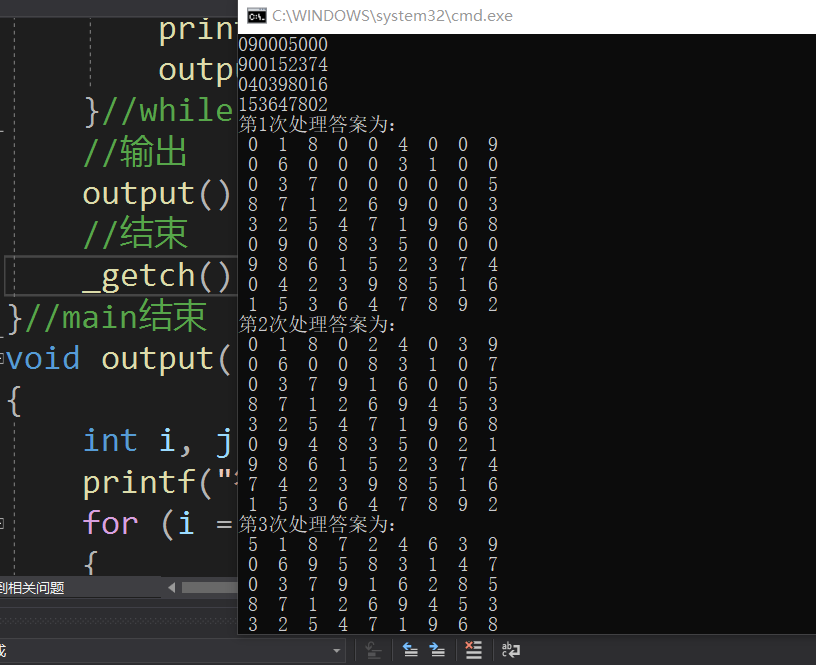
经过不断的更改代码的小错误终于代码可以运行成功并且没有报错:
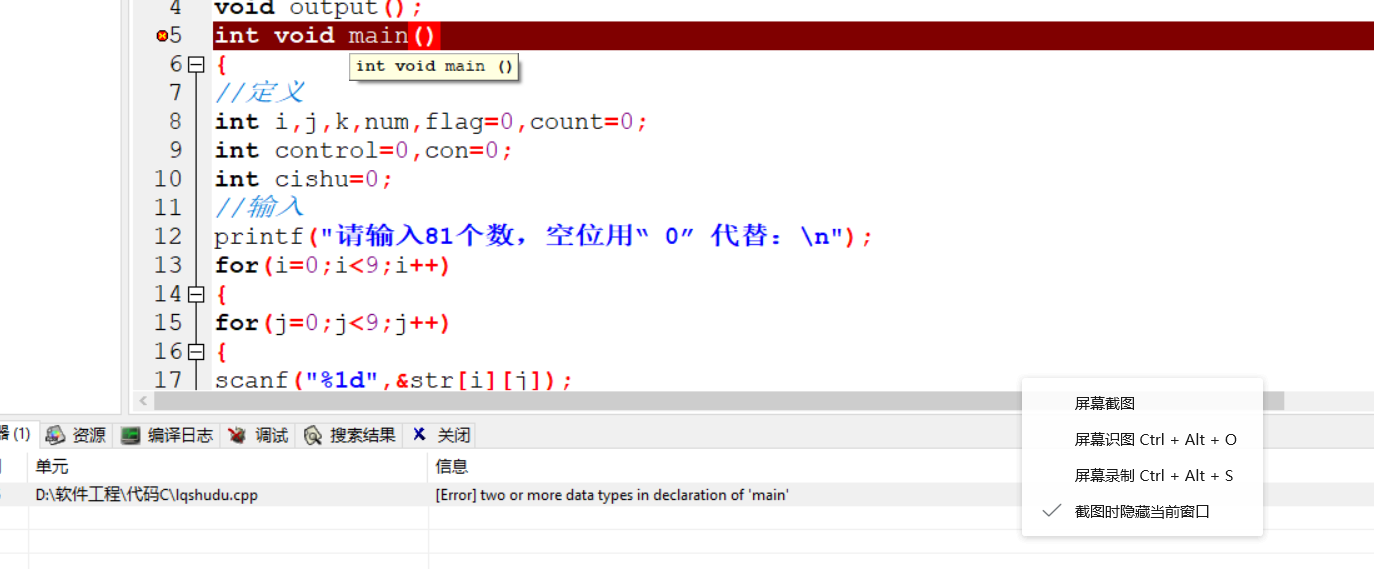
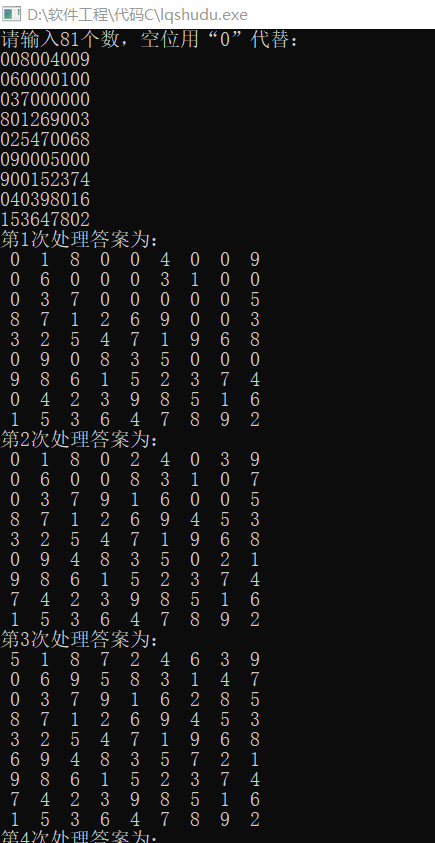
运行结果截图:

代码静态检查并且运行的时候出现了这样的问题:
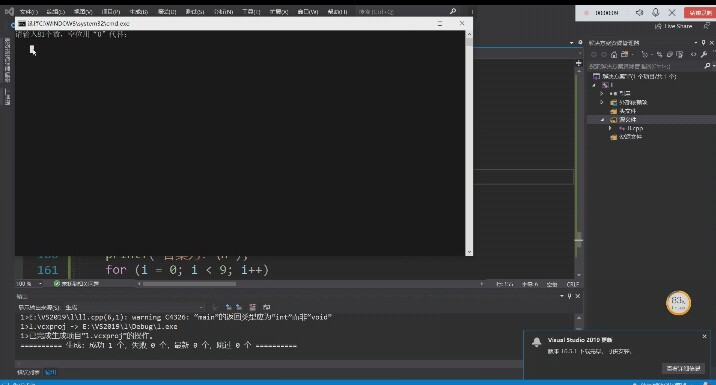

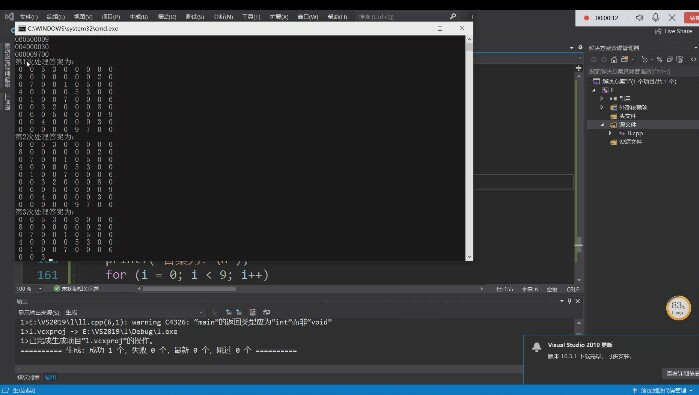
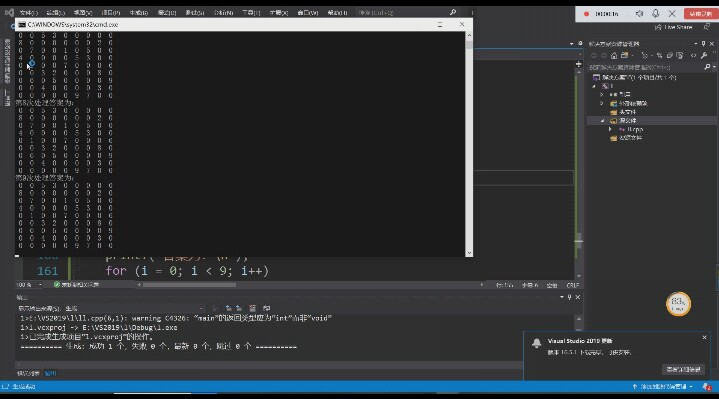
这是因为我发现我那个get的方法出现了异常所以它一直进行处理数据没有停下来过
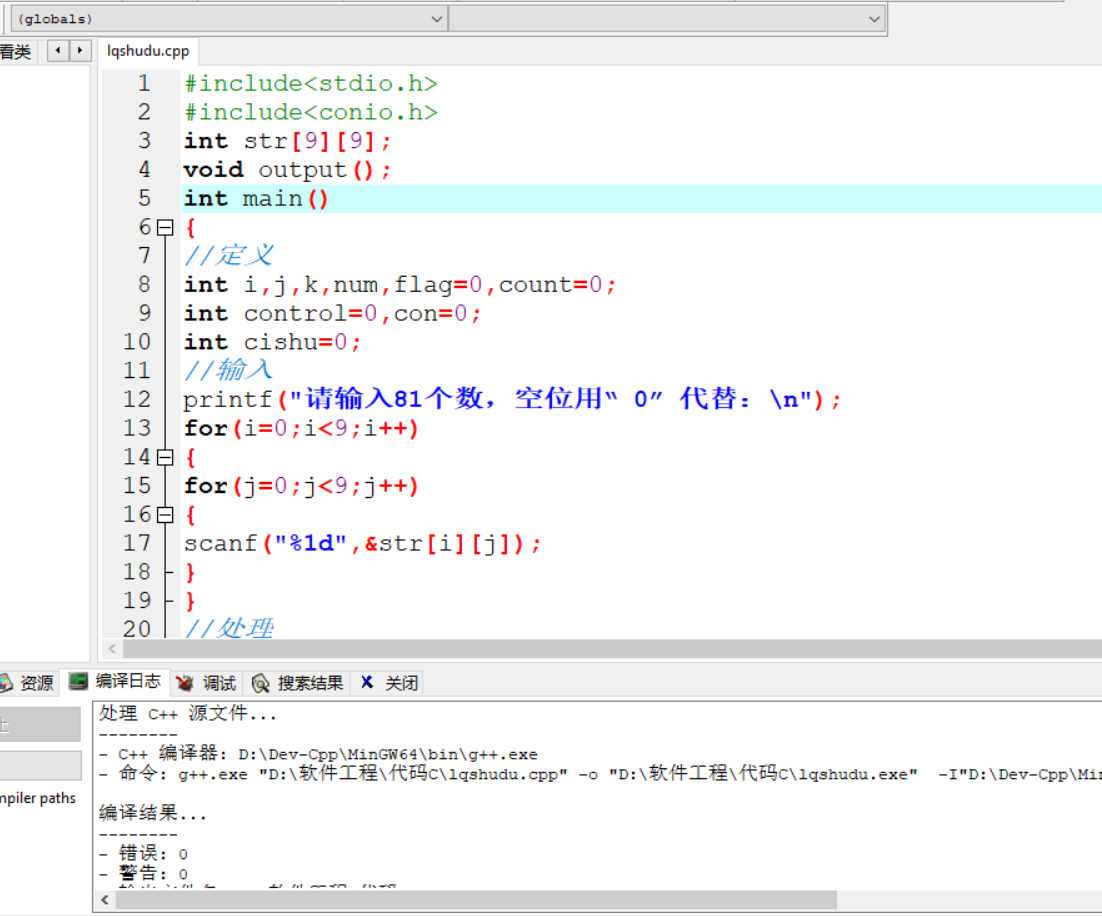
7、代码说明#include<stdio.h>#include<conio.h>
int str[9][9]; void output(); int main() { //定义 int i,j,k,num,flag=0,count=0; int control=0,con=0; int cishu=0; //输入 printf("请输入81个数,空位用“0”代替: "); for(i=0;i<9;i++) { for(j=0;j<9;j++) { scanf("%1d",&str[i][j]); } } //处理
//关键代码由此开始
while(con==0) { con=1; for(i=0;i<9;i++) { for(j=0;j<9;j++) { if(str[i][j]==0) { ////////////////////////////////////////////////////////////////////////// //试值开始 for(num=1;num<=9;num++) { flag=0; //不同于九格 if(i%3==0&&j%3==0) { if(num!=str[i][j+1]&&num!=str[i][j+2]&&num!=str[i+1][j]&&num!=str[i+1][j+1]&&num!=str[i+1][j+2]&&num!=str[i+2][j]&&num!=str[i+2][j+1]&&num!=str[i+2][j+2]) { flag=1; } } else if(i%3==0&&j%3==1) { if(num!=str[i][j+1]&&num!=str[i][j-1]&&num!=str[i+1][j]&&num!=str[i+1][j+1]&&num!=str[i+1][j-1]&&num!=str[i+2][j]&&num!=str[i+2][j+1]&&num!=str[i+2][j-1]) { flag=1; } } else if(i%3==0&&j%3==2) { if(num!=str[i][j-2]&&num!=str[i][j-1]&&num!=str[i+1][j]&&num!=str[i+1][j-2]&&num!=str[i+1][j-1]&&num!=str[i+2][j]&&num!=str[i+2][j-2]&&num!=str[i+2][j-1]) { flag=1; } } else if(i%3==1&&j%3==0) { if(num!=str[i][j+1]&&num!=str[i][j+2]&&num!=str[i+1][j]&&num!=str[i+1][j+1]&&num!=str[i+1][j+2]&&num!=str[i-1][j]&&num!=str[i-1][j+1]&&num!=str[i-1][j+2]) { flag=1; } } else if(i%3==1&&j%3==1) { if(num!=str[i][j+1]&&num!=str[i][j-1]&&num!=str[i+1][j]&&num!=str[i+1][j+1]&&num!=str[i+1][j-1]&&num!=str[i-1][j]&&num!=str[i-1][j+1]&&num!=str[i-1][j-1]) { flag=1; } } else if(i%3==1&&j%3==2) { if(num!=str[i][j-2]&&num!=str[i][j-1]&&num!=str[i+1][j]&&num!=str[i+1][j-2]&&num!=str[i+1][j-1]&&num!=str[i-1][j]&&num!=str[i-1][j-2]&&num!=str[i-1][j-1]) { flag=1; } } else if(i%3==2&&j%3==0) { if(num!=str[i][j+1]&&num!=str[i][j+2]&&num!=str[i-2][j]&&num!=str[i-2][j+1]&&num!=str[i-2][j+2]&&num!=str[i-1][j]&&num!=str[i-1][j+1]&&num!=str[i-1][j+2]) { flag=1; } } else if(i%3==2&&j%3==1) { if(num!=str[i][j+1]&&num!=str[i][j-1]&&num!=str[i-2][j]&&num!=str[i-2][j+1]&&num!=str[i-2][j-1]&&num!=str[i-1][j]&&num!=str[i-1][j+1]&&num!=str[i-1][j-1]) { flag=1; } } else if(i%3==2&&j%3==2) { if(num!=str[i][j-2]&&num!=str[i][j-1]&&num!=str[i-2][j]&&num!=str[i-2][j-2]&&num!=str[i-2][j-1]&&num!=str[i-1][j]&&num!=str[i-1][j-2]&&num!=str[i-1][j-1]) { flag=1; } } //不同与九格结束 //不同于行列检测 if(flag==1) { //不同于行 for(k=0;k<9;k++) { if(k!=i) if(num==str[k][j]) { control=1; } } //不同于列 if(control==0) for(k=0;k<9;k++) { if(k!=j) if(num==str[i][k]) { control=1; } } //不同于行列结束 }//不同于行列检测结束 if((control==0)&&(flag==1)) { str[i][j]=num; count++; } control=0; }//试值结束 if(count>1) { str[i][j]=0; } count=0; }//if(str[i][j]==0)控制结束 }//每行中每列处理结束 }//每行处理结束 //检测是否全部赋值 for(i=0;i<9;i++) for(j=0;j<9;j++) { if(str[i][j]==0) { con=0; } } //分次输出 printf("第%d次处理",++cishu); output(); }//while(con)结束 //输出 output(); //结束 getch(); }//main结束
//关键代码到此结束
void output() { int i,j; printf("答案为: "); for(i=0;i<9;i++) { for(j=0;j<9;j++) { printf(" %d ",str[i][j]); } printf(" "); } }
8、心历路程与收获
经过这次作业,我好无力呀,我看了很多网上大牛的代码,(emmmm,啥玩意呀,看不懂啊,上天啊杀了我吧……),然后有些函数得调用还不知道是啥函数,就一个个一个个百度搜索,因为在性能分析那块我的知识有限,他出来的那些图,我不知道如何优化我的代码,就先一步一步试一试修改一下,改着改着我头顶发凉,都报错了,我这……后来运行的时候出现的语法错误呀,就算语法修改成功啦,结果就一直在哪里处理下去,一直循环下去,就不见他停下来过,说实话改怕了,索性就不改了,就那样吧,作业时间也快用完啦,问了一些学这个的朋友(小牛)我也还是没搞明白,然后要给出宫格的升阶,我就直接九宫格吧,那些3,6...啥宫格的我没有弄,路漫漫其修远兮啊……

这次的作业让我知道我自己还有好多不足的地方,唉,说多了都是泪,也非常感谢我室友的帮助,教了我很多知识,还有帮我去运行我的代码,虽然这次作业没有很好的完成,也就是没有全部完整的完成,但是在以后的时间我要慢慢的完善他,这不完完全全只是一次作业,这是检测我自己的能力的一种活动,不能抱着应付的态度,好好努力坚持下去吧……

9、 自我评估
| 作业头 | 解题思路描述 | Github项目地址 | PSP表格估计 | PSP表格实际 | 代码如何组织 | 关键函数流程图 | 单元测试设计 | 展示关键代码 | 解释思路与注释说明 | 结合构建之法谈感想 | 总分 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 0.5 | 2 | 0.5 | 0.5 | 0.2 | 0.5 | 0 | 0.5 | 0.5 | 0.2 | 7.4 |