[动态规划]Tak and Cards

题目描述

Tak has N cards. On the i-th (1≤i≤N) card is written an integer xi. He is selecting one or more cards from these N cards, so that the average of the integers written on the selected cards is exactly A. In how many ways can he make his selection?

Constraints
1≤N≤50
1≤A≤50
1≤xi≤50
N,A,xi are integers.
Partial Score
200 points will be awarded for passing the test set satisfying 1≤N≤16.

输入

The input is given from Standard Input in the following format:
N A
x1 x2 … xN

输出

Print the number of ways to select cards such that the average of the written integers is exactly A.

样例输入

4 8
7 9 8 9

样例输出

5

提示

The following are the 5 ways to select cards such that the average is 8:
Select the 3-rd card.
Select the 1-st and 2-nd cards.
Select the 1-st and 4-th cards.
Select the 1-st, 2-nd and 3-rd cards.
Select the 1-st, 3-rd and 4-th cards.

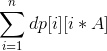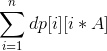思路：很显然，是要求算,这里dp[i][j]表示取i个值和为j的取法数。C(n,1)+C(n,2)+...+C(n,n)=2^n-1，暴力枚举显然超时；考虑找到dp[i][j]的递推式;

容易想到dp[i][j]+=dp[i-1][j-a[k]](k=1~n)，也就是说取i个值和为j的方法数等于取i-1个值和为j-a[k](k=1~n)的方法数之和？显然是不对的，拿样例举例，计算dp[3][24](初值为0)时，在k=1时，dp[3][24]+=dp[2][17]，k=2时，dp[3][24]+=dp[2][15]，k=3时，dp[3][24]+=dp[2][16]...暂且先看k=1~3这一部分，并暂且认为已计算出dp[2][j]的所有结果都是正确的，那dp[3][24]在被k=1~3更新时，很显然能看见取前三个数这种取法被重复计算了三次(也就是这一种取法被视为了三种取法)，那如何避免这样的重复计算呢——在计算dp[i][j]考虑取a[k]时，取满j-a[k]的另外i-1个值只能从a[1~k]之中取。这样的话，就变成了考虑用a[k]更新所有的dp[i][j](i=k~1,j=sum[k]~a[k])（注意用a[k]更新dp[i][j]的顺序——更新dp[i][j]要用到dp[i-1][j-a[k]]，不能用a[k]先把dp[i-1][j-a[k]]给更新了），而不是考虑将dp[i][j]用所有的a[k](k=1~n)去更新；

AC代码：

#include <iostream>
#include<cstdio>
typedef long long ll;
using namespace std;

int a[55];
int sum[55];
ll dp[55][2505];

int main()
{
    int n,A;
    scanf("%d%d",&n,&A);
    for(int i=1;i<=n;i++) {scanf("%d",&a[i]); sum[i]=sum[i-1]+a[i];}
    dp[0][0]=1;
    for(int k=1;k<=n;k++){
        for(int i=k;i>=1;i--){
            for(int j=sum[k];j>=a[k];j--){
                dp[i][j]+=dp[i-1][j-a[k]];
            }
        }
    }
    ll ans=0;
    for(int i=1;i<=n;i++) ans+=dp[i][i*A];
    printf("%lld
",ans);
    return 0;
}

另外，关于动态规划和递推，我已经分不清了(＃°Д°)