参考:
BWT (Burrows–Wheeler_transform)数据转换算法
压缩技术主要的工作方式就是找到重复的模式,进行紧密的编码。
BWT(Burrows–Wheeler_transform)将原来的文本转换为一个相似的文本,转换后使得相同的字符位置连续或者相邻,之后可以使用其他技术如:Move-to-front transform 和 游程编码 进行文本压缩。
1 BWT编码
(1)首先,BWT先对需要转换的文本块,进行循环右移,每次循环一位。可以知道长度为n的文本块,循环n次后重复,这样就得到看n个长度为n的字符串。如下图中的“Rotate Right”列。(其中‘#’作为标识符,不在文本块的字符集中,这样保证n个循环移位后的字符串均布相同。并且定义'#'小于字符集中的任意字符)。
(2)对循环移位后的n个字符串按照字典序排序。如下图中的“Sorted (M)”列。
(3)记录下“Sorted (M)”列中每个字符串的最后一个字符,组成了“L”列。(其中"F"列是“Sorted (M)”列中每个字符串的前缀)
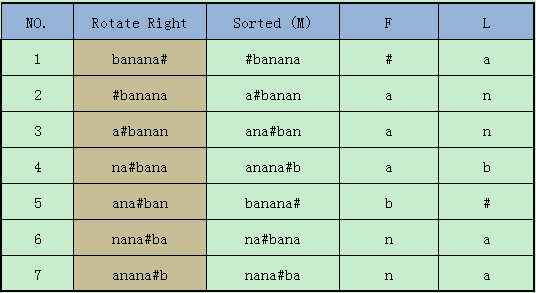
这样,原来的字符串“banana#”就转换为了“annb#aa”。在某些情况下,使用L列进行压缩会有更好的效果。“L”列就是编码的结果。
2 BWT解码
因为进行的是循环移位,且是循环左移注意下面的性质:
1、L的第一个元素是Text中的最后一个元素
2、对于M中的每一行(第一行除外)第一个元素都是最后一个元素的下一个元素。
也就是说,对于文本块而言,同一行中F是L的下一个元素,L是F的前一个元素。
这样,就需要
(1)通过"F"列中的元素,找到他前面的字符,就是对应的同一行“L”列;
(2)通过“L”列中的元素,找到他在“F”列中的对应字符位置。但是“L”中有3个字符a,如何对应F中的3个a呢?因为L是F的前一个元素,多个具有相同前缀的字符串排序,去掉共同前缀后相对次序没有变化。所有遇到多个相同的字符,相对位置不变;
(3)转到(1),直到结束。

因为F列是已经排序的,可以从L列获得,所有只需要保存L列就可以。从L列中的字符获取在F列中的位置时,需要:
(1)前缀和数组,记录小于当前字符的字符数个数。
(2)count计数,计算L中从开始位置到当前字符位置等于该字符的字符数。(保证多个相同字符下"L"到“F”的相对位置不变)。