一、 自己的程序结构分析
1.1 作业一: 简单多项式的求导
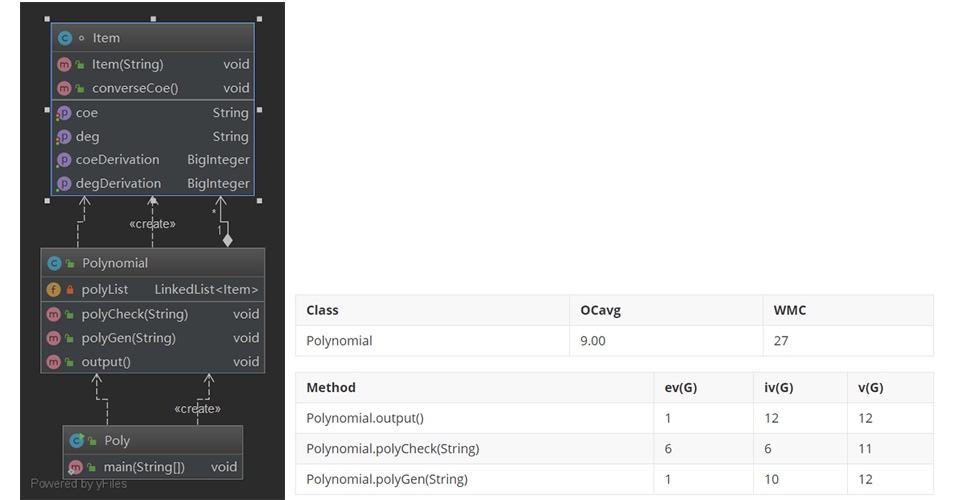
第一次作业和我们在去年在数据结构课上的题目非常相似,所以我自然而然地想到了用链表来存储这样的数据。在本次的作业中,Item作为多项式中细分出的小项,在我的程序中发挥着类似于结构体的作用。但还是有着一些不一样的地方,每一个实例化的Item作为一个独立的对象,可以支持对其自身的求导和输出等操作,而整个多项式的求导等操作也是由这些小项的求导组合而成的。
虽然这次的问题不是很复杂,但是可以看出我的程序的一些方法的复杂度依然是很高的,主要原因在于整个多项式的生成和输出的过程中没有对其进行很好的拆分,完全由一个方法来执行这些操作,造成了很高的复杂度。
1.2 作业二:支持连乘和简单三角函数的无嵌套多项式求导
在第二次作业中,我建立了Poly、Item、Factor类分别对应多项式、项和因子,在一开始设计程序的时候,我希望设计成一个二维的链表结构(即一个链表作为另一个链表的项)以求兼容下一次作业中可能出现的嵌套求导的形式,最终在考虑了实现的难度和本次作业的要求之后决定本次作业先使用相较简单的三元组的形式来完成。
在最终写好的程序中,Factor对应于每个因子的建立和输出,Item对应于每个项的建立和输出。由于采用了三元组的方式来进行整理,所以最后的输出实际上是以Item为单位的,也就是说Factor这个类的设置其实是不必要的。
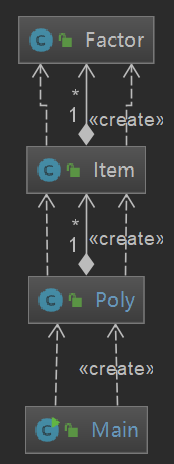
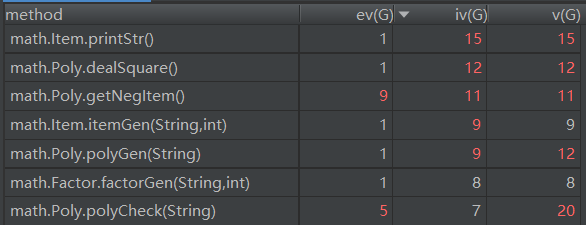
通过复杂度分析我们可以发现,本次作业和第一次作业出现了类似的问题,一些生成、输出、和优化操作的复杂度太高(事实证明本次就有Bug出现在复杂度很高的dealSquare()方法中),一个类中也集成了太多的方法进来。
| Class | OCavg | WMC |
|---|---|---|
| math.Factor | 1.78 | 16.0 |
| math.Item | 3.08 | 40.0 |
| math.Main | 2.0 | 2.0 |
| math.Poly | 6.625 | 53.0 |
从对于类的分析中也可以看出来,在本次的作业中,Item和Poly这两个类承担了太多的复杂性工作,耦合性高。在之后的设计中,要尽力避免出现这样的情况,逐步降低程序中每个类的耦合性。
在本次作业的优化中,主要考虑了合并同类项和三角函数化简两个方面。由于使用了链表来存储三元组结构,所以这两个方面的化简都采用了两重循环的方式来进行。三角函数化简主要依赖了、、这三个公式,考虑到一次遍历可能无法将可以合并项消到最简,所以手动增加了两次扫描。
1.3 作业三: 支持连乘和三角函数的嵌套多项式求导
在第三次作业中,经过讨论和思考,没有选用在上次作业的时候想到的二维链表结构,转向了使用表达式树来构建(二者其实是相似的)。
由于在数据结构课程中我们曾经学到过前缀表达式转为后缀表达式和后缀表达式转化为表达式树,为了方便调试,我首先将输入的表达式(在进行正确性判断后)转化为后缀表达式,再将其转化为表达式树。这个时候,表达式树上的叶子节点只能是常数或者是自变量x的幂次,其他结点为运算符。根据链式求导的原则,一个子树的导数一定能够用这个子树的两个子树表示出来,所以便可以使用递归的方法对整棵树进行求导。
由于有了第二次作业中,优化引入bug的经历,在这次作业中,我只进行了少量的优化:
- 如果某个结点的子树中有常数0,则将这个节点置为常数0。由于采用了中序遍历的方式,所以可以化简程序中所有的乘0操作。
- 同理化简了乘1、加0、常数相加、常数相乘等情况
事实证明,这些化简一分性能分也没有拿到。主要原因在于为了保证程序的正确性,我输出了大量的括号,且对于括号基本没有进行化简(上次的作业中化简部分有了问题,这次就Follow Heart了)
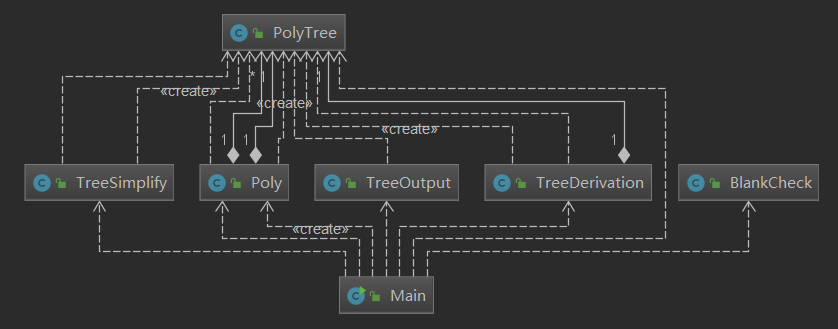
这个是本次作业的类图,PolyTree为叶节点类。程序依然是扁平化的风格,没有层次感。对于树的求导、化简、输出都是由Main进行统一的管理,导致了Main需要参与到具体的实现中。
而从多项式的分离和正确性判断到前缀转后缀的操作再到表达式树的生成,这一系列复杂的操作,我都交给了Poly这个类来完成,直接导致了它的复杂度飙升。程序中很多还是沿用了面向过程的思维方式,导致在程序刚写完时Poly类中有一些方法非常长,对于Debug造成了很大的困难(也使得即使再调试和测试完成后,对于它的正确性还是有点虚)。
| Method | ev(G) | iv(G) | v(G) |
|---|---|---|---|
| Poly.suffixListGen() | 11.0 | 20.0 | 20.0 |
| Poly.prefixListGen() | 8.0 | 17.0 | 17.0 |
| TreeOutput.TreeOut(PolyTree) | 15.0 | 15.0 | 15.0 |
| TreeSimplify.mul(PolyTree) | 5.0 | 14.0 | 14.0 |
| Class | OCavg | WMC |
|---|---|---|
| Poly | 6.4 | 64.0 |
从方法和类的复杂度分析中也可也看出,Poly绝对是复杂度重灾区,它对于整个程序的稳定性起到了非常不好的作用。
二、 出现的Bug分析
2.1 双重循环--Bug会藏得很深
在第二次作业中,我使用了链表来存储多项式中的一个个三元组。所以在进行同类项合并的时候,我选择了使用双重循环来寻找符合的项。但是在遍历的过程中,我为了减少iitem实例化的次数,将它的实例化放在第一层循环中。但是我会在内层中修改i对应链表中项的值,这也导致了j在继续运行的过程中,程序在内层循环中拿到的值是旧的iitem对应的属性。这个Bug在写程序的时候没有预料到,后来在互测的过程中测出来了也没有什么办法。但是在之后写程序的时候对于这样容易出现问题的地方一定要小心谨慎。
for (int i = 0; i < outputList.size(); i++) {
Item iitem = outputList.get(i);
for (int j = i + 1; j < outputList.size(); j++) {
Item jitem = outputList.get(j);
2.2 手抖不是Bug的借口
在作业二的优化中,我将
.setCosdeg(jcosdeg) 写成了 .setSindeg(jcosdeg)
造成了严重的错误。这也给之后的程序设计敲响警钟,一定要选择不易更不易出错的方式来完成程序,一定要在写完后仔细地验证复核自己的程序。
2.3 新加入功能时一定要考虑可能产生的影响
在第三次作业中,我使用了
int deg = Integer.parseInt(numMatcher.group());
if (deg > 10000 || deg <= 0) {
wrongFormat();
}
来判断指数不合法的情况。在自己测试的时候注意到了int型的deg可能出现超出范围的报错,所以在最后提交的时候加入了:
if (numMatcher.group().length() > 6) {
wrongFormat();
}
来剔除位数超标导致int爆掉的情况。但是在互测的过程中,同组同学构造了”x^0000006“这样的样例。这样的情况确实是在加这句话的时候没有想到的。这次的bug也说明,新加入的代码很可能会影响原有程序的正确性,所以在新加入时一定要做充分的思考和验证。
在测试过程中,主要是使用在测试自己程序时使用的测试样例进行对拍。在阅读同组同学代码的过程中,可能也更能做到一种旁观者清的态度,来考量他在什么地方考虑地不够周全,从而针对性地构造测试样例。
三、 在互测中找出的Bug分析
在前期的作业中,互测中能找到的问题大多数是对于WRONG FORMAT的判断,一旦情况没有讨论充足便很可能会发生错误。在第一次作业的时候,曾经看到一个同学是使用正则来举反例判断式子的有效性,但是却漏掉了很多情况导致可以针对性地构造bug来Hack。后期的作业WF失误的情况逐渐减少,但是随着代码量的加大和需要解决的问题越发复杂,一些同学在功能性上出现了错误。如第二次作业中出现有的同学在结果为0的时候不输出的情况,在第三次作业中看到有同学可以进行很好的化简但是会出现指数少1的情况。这些错误都在提示我们充分测试的必要性,只有考虑各种边界性的样例,对自己的程序构造充分的测试,才能一步步增强对于自己的程序的信心。
在第一次作业中看到有同学因为使用大正则爆栈的问题,因而也了解到了java的正则表达匹配在普通模式下可能递归层数过多,这也提醒了自己在之后使用正则匹配时要注意使用方式,提防类似的事故发生。
四、 重构说明
其实这几次作业比较遗憾的是很少用到面向对象的一些基本思想,虽然我们在课堂上和书本上已经学了相关的知识,但是到了自己下笔去写,又回到了面向过程的老路上去了。对于第三次作业,希望能够将不同功能的因子类剥离,同时分拆程序中复杂的类和方法,降低程序的复杂度。
这三次作业整体看来,并没有在一开始形成一个比较明确的思路和架构,致使每一次的作业都要事实上地重写。从这三周的学习过程中,也能感觉到自己对于面向对象的理解还是不是很足够的,这也是下一个阶段的学习需要补足的部分。