Trie(字典树)的基本操作与应用（一般与字符串前缀相关）

字典树是一种树型结构，可用于较高效的处理字符串前缀相关问题，实际应用和搜索引擎密切相关。

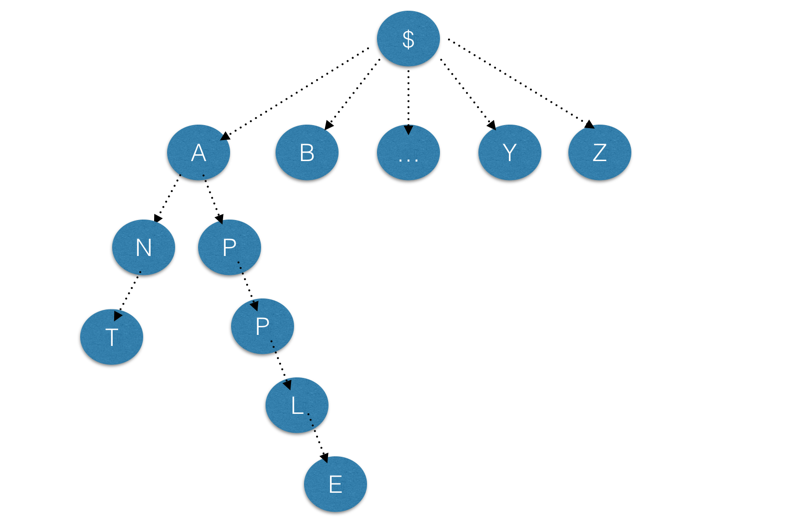
此图即为字典树，根节点不存储字符，每个根节点有26（52）颗子树。

建树代码：

const int maxn = 1e6 + 5;
int v[maxn],tree[maxn][26]; //tree里存每个节点的编号，v数组里存各个编号对应的节点的（所表示字符串or字符串前缀）的个数
int dep[maxn];
int nowrt;
int k,t,n;

void add(string s){
    int root = 1;
    for(int i = 0; i < s.size(); i++){
        if(tree[root][s[i]-'A']){
            root = tree[root][s[i]-'A'];
        }
        else{
            nowrt++;
            tree[root][s[i]-'A'] = nowrt;
            dep[nowrt] = dep[root] + 1; //dep数组保存的是层数，即某编号表示的字符串（或其某个前缀）的长度
            root = nowrt;
        }
        v[root]++;
    }
}

tree数组即是这颗字典树，root的子树存在tree[nowrt]里，（nowrt随新扩展的子树其值不断增大，子树编号在数组中的扩展随新增的顺序而增大，而与其层数无关）

tree[y][x]存储的是 字典(子)树y的子树x的编号，而每个节点的编号则作为v的下标查询此处的字符串（或某字符串前缀出现的次数）

dep存的是某编号表示的字符串（节点）所在的树中的层数（非必要）

查询操作：

bool find(string s){
    int root = 1;
    for(int i = 0; i < s.size(); i++)
        if(tree[root][s[i]-'A'])
            root = tree[root][s[i]-'A'];
        else
            return false;
        return true;
}

这个比较显然，一个个字符的进行查询，如果没有这个节点就直接返回false，否则继续直到查询完为止

时间复杂度O(length)

一道题：

Prepare for CET-6

In order to prepare the CET-6 exam, xiaoming is reciting English words recently. Because he is already very clever, he can only recite n words to get full marks. He is going to memorize K words every day. But he found that if the length of the longest prefix shared by all the strings in that day is a​i​​, then he could get a​i​​ laziness value. The lazy xiaoming must hope that the lazier the better, so what is the maximum laziness value he can get?

For example:

The group {RAINBOW, RANK, RANDOM, RANK} has a laziness value of 2 (the longest prefix is 'RA').

The group {FIRE, FIREBALL, FIREFIGHTER} has a laziness value of 4 (the longest prefix is 'FIRE').

The group {ALLOCATION, PLATE, WORKOUT, BUNDLING} has a laziness value of 0 (the longest prefix is '').

Input:

The first line of the input gives the number of test cases, T. T test cases follow. Each test case begins with a line containing the two integers N and K. Then, N lines follow, each containing one of Pip's strings.

2≤N≤10​5​​

2≤K≤N

Each of Pip's strings contain at least one character.

Each string consists only of letters from A to Z.

K divides N.

The total number of characters in Pip's strings across all test cases is at most .

Output:

For each test case, output one line containing Case #x: y, where x is the test case number (starting from 1) and y is the maximum sum of scores possible.

 题意就是给出t组case，每组n个字符串，分成n/k组后，求所有组前缀字符个数之和的最大值

这里给出的思路是：dfs搜字典树（这里用dfs的原因是我们要求最大值，要尽量先选出字符串前缀相同长度大的字符串）

int dfs(int x){
    int ans = 0, num = v[x];
    for(int i = 0; i < 26; i++){
        if(tree[x][i] && v[tree[x][i]] >= k)
        ans += dfs(tree[x][i]); //向下dfs直至叶节点
        num -= v[tree[x][i]]/k*k; //该节点减去其所有(被匹配过了的）子节点的个数
    }
    return ans+(num/k)*(dep[x]）;
}

每个节点的数目num减去其子树已经选走的字符串（因为在存储过程中每个字符的节点都++了，避免重复计算）