P4159 [SCOI2009] 迷路
这道题一个很奇怪的特点就是边权是以字符串的形式给的,也就是说两点之间的距离小于等于9。
不妨先考虑当路径长度都是1的情况,那么题目要求的其实就是走了(t)步到达(n)点的方案数
设(f[i][j][t])表示从(i)到(j)恰好走了(t)步的方案数,则
(f[i][j][t] = sumlimits_{k=1}^nf[i][k][t-1]*f[k][j][1])
发现这不正好是矩阵乘法的公式吗。
设(t)时刻的矩阵为(f_t),则(f_t=f_{t-1}*f_1),也就是(f_t=f_1^t),直接矩阵快速幂搞一下就好了,而(f_1)也就是题中所给的邻接矩阵。
回到原来的问题上,边权小于等于(9)怎么做?
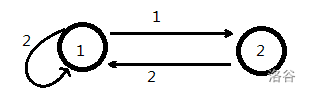
有一个想法就是把一个点看成(9)个点,在这九个点之间连边。这样就把问题转化成了先前我们讨论的问题。那么接下来考虑的就是如何拆点。不妨先考虑简单的情况,两个点,边权最大为(2)。
有如下矩阵:
[egin{Bmatrix}
2&1\
2&0
end{Bmatrix}
]
画出图就是这样
拆点后
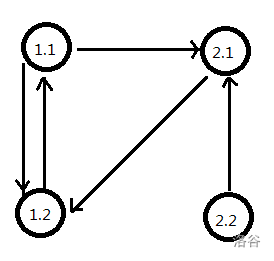
这里每条边的边权都是1,其中点(1.1)和(2.1)表示实际的点,(1.2)和(2.2)表示拆出来的点。
以此类推到九个点也是一样的
#include<bits/stdc++.h>
using namespace std;
const int N = 105;
const int mod = 2009;
int n, t, sz;
struct martix
{
int m[N][N];
}e, a;
martix cheng(martix x, martix y)
{
martix c;
for(int i = 1; i <= sz; i ++)
for(int j = 1; j <= sz; j ++) c.m[i][j] = 0;
for(int i = 1; i <= sz; i ++)
for(int j = 1; j <= sz; j ++)
for(int k = 1; k <= sz; k ++)
c.m[i][j] = (c.m[i][j] + x.m[i][k] * y.m[k][j] % mod) % mod;
return c;
}
martix pow(martix x, int y)
{
martix ans = e;
while(y)
{
if(y & 1) ans = cheng(ans, x);
x = cheng(x, x);
y >>= 1;
}
return ans;
}
char s[N];
int main()
{
scanf("%d%d", &n, &t);
sz = n * 10;
for(int i = 1; i <= sz; i ++)
e.m[i][i] = 1;
for(int i = 1; i <= n; i ++)
{
int now = (i - 1) * 10;
for(int j = 2; j <= 9; j ++)
a.m[j + now - 1][j + now] = 1;
}
for(int i = 1; i <= n; i ++)
{
scanf("%s", s + 1);
int now = (i - 1) * 10;
for(int j = 1; j <= n; j ++)
{
if(s[j] == '0') continue;
int to = s[j] - '0';
a.m[now + 9][j * 10 - to] = 1;
}
}
e = pow(a, t);
printf("%d
", e.m[9][(n-1) * 10 + 9]);
}