强连通分量tarjan模板复习

对于一个有向图定点的子集，在该子集中任取两点u与v，都能找到一条从u到v的路径，则称该子集是强连通的。若该集合加入到任意点集中，它都不再强连通，则称这个子集是原图的一个强连通分量。任意一张图都可以分解成若干个不相交的强连通分量。这是强连通分量分解。把分解后的强连通分量缩成一个顶点，就可以得到一个有向无环图。

如图：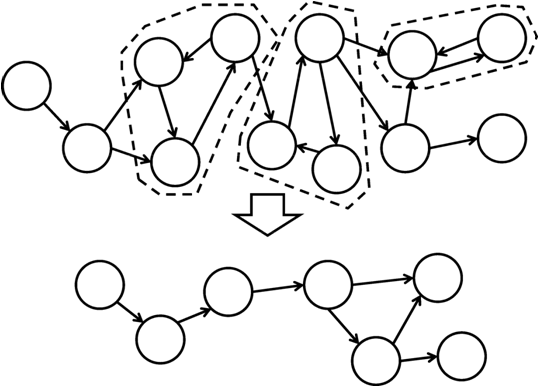

求一张图的强连通分量的个数，常用tarjan算法，它是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。

模板如下：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>
using namespace std;
int n,m;
struct node{
    int fr,to;
}ed[50001];
bool vis[10001];
int dfs[10001],stack[10001],head[10001],low[10005];
int tot=0,ans=0,in=0,num=0;
void add(int u,int v){
    ed[++num].fr=head[u];head[u]=num;ed[num].to=v;
}
void tarjan(int x){
    dfs[x]=low[x]=++tot;
    stack[++in]=x;
    vis[stack[in]]=1;
    int i;
    for(i=head[x];i;i=ed[i].fr){
        if(!dfs[ed[i].to]){
            tarjan(ed[i].to);
        }
        if(vis[ed[i].to]){
            low[x]=min(low[x],low[ed[i].to]);
        }
    }
    if(low[x]==dfs[x]){
        for(++ans;stack[in+1]!=x;)  vis[stack[in--]]=0;
    }
}
int main(){
    scanf("%d%d",&n,&m);
    int i;
    for(i=1;i<=m;i++){
        int x,y;
        scanf("%d%d",&x,&y);
        add(x,y);
    }
    for(i=1;i<=n;i++)  if(!dfs[i])  tarjan(i);
    printf("%d\n",ans);
    return 0;
}