Ceres Solver

// Ceres Solver - A fast non-linear least squares minimizer
// Copyright 2015 Google Inc. All rights reserved.
// http://ceres-solver.org/
//
// Redistribution and use in source and binary forms, with or without
// modification, are permitted provided that the following conditions are met:
//
// * Redistributions of source code must retain the above copyright notice,
//   this list of conditions and the following disclaimer.
// * Redistributions in binary form must reproduce the above copyright notice,
//   this list of conditions and the following disclaimer in the documentation
//   and/or other materials provided with the distribution.
// * Neither the name of Google Inc. nor the names of its contributors may be
//   used to endorse or promote products derived from this software without
//   specific prior written permission.
//
// THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS"
// AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE
// IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE
// ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR CONTRIBUTORS BE
// LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR
// CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF
// SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS
// INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN
// CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE)
// ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE
// POSSIBILITY OF SUCH DAMAGE.
//
// Author: sameeragarwal@google.com (Sameer Agarwal)
//
// An example program that minimizes Powell's singular function.
//
//   F = 1/2 (f1^2 + f2^2 + f3^2 + f4^2)
//
//   f1 = x1 + 10*x2;
//   f2 = sqrt(5) * (x3 - x4)
//   f3 = (x2 - 2*x3)^2
//   f4 = sqrt(10) * (x1 - x4)^2
//
// The starting values are x1 = 3, x2 = -1, x3 = 0, x4 = 1.
// The minimum is 0 at (x1, x2, x3, x4) = 0.
//
// From: Testing Unconstrained Optimization Software by Jorge J. More, Burton S.
// Garbow and Kenneth E. Hillstrom in ACM Transactions on Mathematical Software,
// Vol 7(1), March 1981.

#include <vector>
#include "ceres/ceres.h"
#include "gflags/gflags.h"
#include "glog/logging.h"

using ceres::AutoDiffCostFunction;
using ceres::CostFunction;
using ceres::Problem;
using ceres::Solver;
using ceres::Solve;

struct F1 {
  template <typename T> bool operator()(const T* const x1,
                                        const T* const x2,
                                        T* residual) const {
    // f1 = x1 + 10 * x2;
    residual[0] = x1[0] + 10.0 * x2[0];
    return true;
  }
};

struct F2 {
  template <typename T> bool operator()(const T* const x3,
                                        const T* const x4,
                                        T* residual) const {
    // f2 = sqrt(5) (x3 - x4)
    residual[0] = sqrt(5.0) * (x3[0] - x4[0]);
    return true;
  }
};

struct F3 {
  template <typename T> bool operator()(const T* const x2,
                                        const T* const x3,
                                        T* residual) const {
    // f3 = (x2 - 2 x3)^2
    residual[0] = (x2[0] - 2.0 * x3[0]) * (x2[0] - 2.0 * x3[0]);
    return true;
  }
};

struct F4 {
  template <typename T> bool operator()(const T* const x1,
                                        const T* const x4,
                                        T* residual) const {
    // f4 = sqrt(10) (x1 - x4)^2
    residual[0] = sqrt(10.0) * (x1[0] - x4[0]) * (x1[0] - x4[0]);
    return true;
  }
};

DEFINE_string(minimizer, "trust_region",
              "Minimizer type to use, choices are: line_search & trust_region");

int main(int argc, char** argv) {
  CERES_GFLAGS_NAMESPACE::ParseCommandLineFlags(&argc, &argv, true);
  google::InitGoogleLogging(argv[0]);

  double x1 =  3.0;
  double x2 = -1.0;
  double x3 =  0.0;
  double x4 =  1.0;

  Problem problem;
  // Add residual terms to the problem using the using the autodiff
  // wrapper to get the derivatives automatically. The parameters, x1 through
  // x4, are modified in place.
  problem.AddResidualBlock(new AutoDiffCostFunction<F1, 1, 1, 1>(new F1),
                           NULL,
                           &x1, &x2);
  problem.AddResidualBlock(new AutoDiffCostFunction<F2, 1, 1, 1>(new F2),
                           NULL,
                           &x3, &x4);
  problem.AddResidualBlock(new AutoDiffCostFunction<F3, 1, 1, 1>(new F3),
                           NULL,
                           &x2, &x3);
  problem.AddResidualBlock(new AutoDiffCostFunction<F4, 1, 1, 1>(new F4),
                           NULL,
                           &x1, &x4);

  Solver::Options options;
  LOG_IF(FATAL, !ceres::StringToMinimizerType(FLAGS_minimizer,
                                              &options.minimizer_type))
      << "Invalid minimizer: " << FLAGS_minimizer
      << ", valid options are: trust_region and line_search.";

  options.max_num_iterations = 100;
  options.linear_solver_type = ceres::DENSE_QR;
  options.minimizer_progress_to_stdout = true;

  std::cout << "Initial x1 = " << x1
            << ", x2 = " << x2
            << ", x3 = " << x3
            << ", x4 = " << x4
            << "
";

  // Run the solver!
  Solver::Summary summary;
  Solve(options, &problem, &summary);

  std::cout << summary.FullReport() << "
";
  std::cout << "Final x1 = " << x1
            << ", x2 = " << x2
            << ", x3 = " << x3
            << ", x4 = " << x4
            << "
";
  return 0;
}

 求导

High lever advice

1.Use Automatic Derivatives.

2.In some cases,it may be worth use Analytic Derivatives.

3.Avoid Numeric Derivations. Use it as a measure of last resort,mostly to interface with extennal libraries.

 Analytic Derivatives 手动推导导数表达式

To get the best performance out of analytically computed derivatives, one usually needs to optimize the code to account for common sub-expressions.

Numeric Derivatives 数值求导

1.Forward Differences

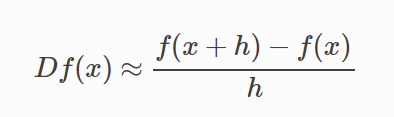
struct Rat43CostFunctor {
  Rat43CostFunctor(const double x, const double y) : x_(x), y_(y) {}

  bool operator()(const double* parameters, double* residuals) const {
    const double b1 = parameters[0];
    const double b2 = parameters[1];
    const double b3 = parameters[2];
    const double b4 = parameters[3];
    residuals[0] = b1 * pow(1.0 + exp(b2 -  b3 * x_), -1.0 / b4) - y_;
    return true;
  }

  const double x_;
  const double y_;
}

CostFunction* cost_function =
  new NumericDiffCostFunction<Rat43CostFunctor, FORWARD, 1, 4>(
    new Rat43CostFunctor(x, y));

 The error in the forward difference formula is O(h)

2.Central Differences

 

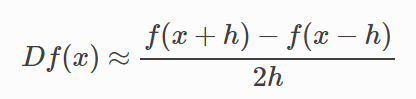
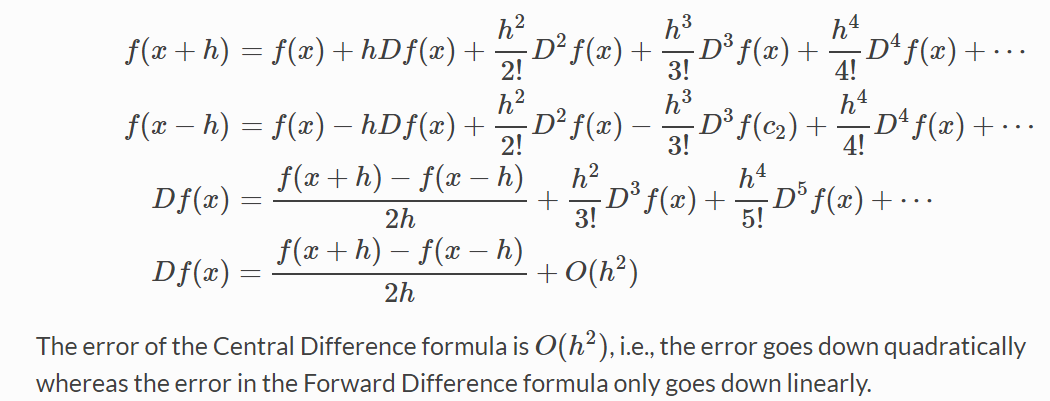
 3.Ridders' Method

 

 Automatic Derivatives 自动微分

Automatic derivatives is a technique that can compute exact derivatives.

struct Rat43CostFunctor {
  Rat43CostFunctor(const double x, const double y) : x_(x), y_(y) {}

  template <typename T>
  bool operator()(const T* parameters, T* residuals) const {
    const T b1 = parameters[0];
    const T b2 = parameters[1];
    const T b3 = parameters[2];
    const T b4 = parameters[3];
    residuals[0] = b1 * pow(1.0 + exp(b2 -  b3 * x_), -1.0 / b4) - y_;
    return true;
  }

  private:
    const double x_;
    const double y_;
};


CostFunction* cost_function =
      new AutoDiffCostFunction<Rat43CostFunctor, 1, 4>(
        new Rat43CostFunctor(x, y));

 

// Ceres Solver - A fast non-linear least squares minimizer
// Copyright 2015 Google Inc. All rights reserved.
// http://ceres-solver.org/
//
// Redistribution and use in source and binary forms, with or without
// modification, are permitted provided that the following conditions are met:
//
// * Redistributions of source code must retain the above copyright notice,
//   this list of conditions and the following disclaimer.
// * Redistributions in binary form must reproduce the above copyright notice,
//   this list of conditions and the following disclaimer in the documentation
//   and/or other materials provided with the distribution.
// * Neither the name of Google Inc. nor the names of its contributors may be
//   used to endorse or promote products derived from this software without
//   specific prior written permission.
//
// THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS"
// AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE
// IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE
// ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR CONTRIBUTORS BE
// LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR
// CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF
// SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS
// INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN
// CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE)
// ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE
// POSSIBILITY OF SUCH DAMAGE.
//
// Author: keir@google.com (Keir Mierle)
//
// A simple implementation of N-dimensional dual numbers, for automatically
// computing exact derivatives of functions.
//
// While a complete treatment of the mechanics of automatic differentiation is
// beyond the scope of this header (see
// http://en.wikipedia.org/wiki/Automatic_differentiation for details), the
// basic idea is to extend normal arithmetic with an extra element, "e," often
// denoted with the greek symbol epsilon, such that e != 0 but e^2 = 0. Dual
// numbers are extensions of the real numbers analogous to complex numbers:
// whereas complex numbers augment the reals by introducing an imaginary unit i
// such that i^2 = -1, dual numbers introduce an "infinitesimal" unit e such
// that e^2 = 0. Dual numbers have two components: the "real" component and the
// "infinitesimal" component, generally written as x + y*e. Surprisingly, this
// leads to a convenient method for computing exact derivatives without needing
// to manipulate complicated symbolic expressions.
//
// For example, consider the function
//
//   f(x) = x^2 ,
//
// evaluated at 10. Using normal arithmetic, f(10) = 100, and df/dx(10) = 20.
// Next, argument 10 with an infinitesimal to get:
//
//   f(10 + e) = (10 + e)^2
//             = 100 + 2 * 10 * e + e^2
//             = 100 + 20 * e       -+-
//                     --            |
//                     |             +--- This is zero, since e^2 = 0
//                     |
//                     +----------------- This is df/dx!
//
// Note that the derivative of f with respect to x is simply the infinitesimal
// component of the value of f(x + e). So, in order to take the derivative of
// any function, it is only necessary to replace the numeric "object" used in
// the function with one extended with infinitesimals. The class Jet, defined in
// this header, is one such example of this, where substitution is done with
// templates.
//
// To handle derivatives of functions taking multiple arguments, different
// infinitesimals are used, one for each variable to take the derivative of. For
// example, consider a scalar function of two scalar parameters x and y:
//
//   f(x, y) = x^2 + x * y
//
// Following the technique above, to compute the derivatives df/dx and df/dy for
// f(1, 3) involves doing two evaluations of f, the first time replacing x with
// x + e, the second time replacing y with y + e.
//
// For df/dx:
//
//   f(1 + e, y) = (1 + e)^2 + (1 + e) * 3
//               = 1 + 2 * e + 3 + 3 * e
//               = 4 + 5 * e
//
//               --> df/dx = 5
//
// For df/dy:
//
//   f(1, 3 + e) = 1^2 + 1 * (3 + e)
//               = 1 + 3 + e
//               = 4 + e
//
//               --> df/dy = 1
//
// To take the gradient of f with the implementation of dual numbers ("jets") in
// this file, it is necessary to create a single jet type which has components
// for the derivative in x and y, and passing them to a templated version of f:
//
//   template<typename T>
//   T f(const T &x, const T &y) {
//     return x * x + x * y;
//   }
//
//   // The "2" means there should be 2 dual number components.
//   // It computes the partial derivative at x=10, y=20.
//   Jet<double, 2> x(10, 0);  // Pick the 0th dual number for x.
//   Jet<double, 2> y(20, 1);  // Pick the 1st dual number for y.
//   Jet<double, 2> z = f(x, y);
//
//   LOG(INFO) << "df/dx = " << z.v[0]
//             << "df/dy = " << z.v[1];
//
// Most users should not use Jet objects directly; a wrapper around Jet objects,
// which makes computing the derivative, gradient, or jacobian of templated
// functors simple, is in autodiff.h. Even autodiff.h should not be used
// directly; instead autodiff_cost_function.h is typically the file of interest.
//
// For the more mathematically inclined, this file implements first-order
// "jets". A 1st order jet is an element of the ring
//
//   T[N] = T[t_1, ..., t_N] / (t_1, ..., t_N)^2
//
// which essentially means that each jet consists of a "scalar" value 'a' from T
// and a 1st order perturbation vector 'v' of length N:
//
//   x = a + sum_i v[i] t_i
//
// A shorthand is to write an element as x = a + u, where u is the perturbation.
// Then, the main point about the arithmetic of jets is that the product of
// perturbations is zero:
//
//   (a + u) * (b + v) = ab + av + bu + uv
//                     = ab + (av + bu) + 0
//
// which is what operator* implements below. Addition is simpler:
//
//   (a + u) + (b + v) = (a + b) + (u + v).
//
// The only remaining question is how to evaluate the function of a jet, for
// which we use the chain rule:
//
//   f(a + u) = f(a) + f'(a) u
//
// where f'(a) is the (scalar) derivative of f at a.
//
// By pushing these things through sufficiently and suitably templated
// functions, we can do automatic differentiation. Just be sure to turn on
// function inlining and common-subexpression elimination, or it will be very
// slow!
//
// WARNING: Most Ceres users should not directly include this file or know the
// details of how jets work. Instead the suggested method for automatic
// derivatives is to use autodiff_cost_function.h, which is a wrapper around
// both jets.h and autodiff.h to make taking derivatives of cost functions for
// use in Ceres easier.

#ifndef CERES_PUBLIC_JET_H_
#define CERES_PUBLIC_JET_H_

#include <cmath>
#include <iosfwd>
#include <iostream>  // NOLINT
#include <limits>
#include <string>

#include "Eigen/Core"
#include "ceres/internal/port.h"

namespace ceres {

template <typename T, int N>
struct Jet {
  enum { DIMENSION = N };
  typedef T Scalar;

  // Default-construct "a" because otherwise this can lead to false errors about
  // uninitialized uses when other classes relying on default constructed T
  // (where T is a Jet<T, N>). This usually only happens in opt mode. Note that
  // the C++ standard mandates that e.g. default constructed doubles are
  // initialized to 0.0; see sections 8.5 of the C++03 standard.
  Jet() : a() {
    v.setZero();
  }

  // Constructor from scalar: a + 0.
  explicit Jet(const T& value) {
    a = value;
    v.setZero();
  }

  // Constructor from scalar plus variable: a + t_i.
  Jet(const T& value, int k) {
    a = value;
    v.setZero();
    v[k] = T(1.0);
  }

  // Constructor from scalar and vector part
  // The use of Eigen::DenseBase allows Eigen expressions
  // to be passed in without being fully evaluated until
  // they are assigned to v
  template<typename Derived>
  EIGEN_STRONG_INLINE Jet(const T& a, const Eigen::DenseBase<Derived> &v)
      : a(a), v(v) {
  }

  // Compound operators
  Jet<T, N>& operator+=(const Jet<T, N> &y) {
    *this = *this + y;
    return *this;
  }

  Jet<T, N>& operator-=(const Jet<T, N> &y) {
    *this = *this - y;
    return *this;
  }

  Jet<T, N>& operator*=(const Jet<T, N> &y) {
    *this = *this * y;
    return *this;
  }

  Jet<T, N>& operator/=(const Jet<T, N> &y) {
    *this = *this / y;
    return *this;
  }

  // Compound with scalar operators.
  Jet<T, N>& operator+=(const T& s) {
    *this = *this + s;
    return *this;
  }

  Jet<T, N>& operator-=(const T& s) {
    *this = *this - s;
    return *this;
  }

  Jet<T, N>& operator*=(const T& s) {
    *this = *this * s;
    return *this;
  }

  Jet<T, N>& operator/=(const T& s) {
    *this = *this / s;
    return *this;
  }

  // The scalar part.
  T a;

  // The infinitesimal part.
  //
  // We allocate Jets on the stack and other places they might not be aligned
  // to X(=16 [SSE], 32 [AVX] etc)-byte boundaries, which would prevent the safe
  // use of vectorisation.  If we have C++11, we can specify the alignment.
  // However, the standard gives wide latitude as to what alignments are valid,
  // and it might be that the maximum supported alignment *guaranteed* to be
  // supported is < 16, in which case we do not specify an alignment, as this
  // implies the host is not a modern x86 machine.  If using < C++11, we cannot
  // specify alignment.

#if defined(EIGEN_DONT_VECTORIZE)
  Eigen::Matrix<T, N, 1, Eigen::DontAlign> v;
#else
  // Enable vectorisation iff the maximum supported scalar alignment is >=
  // 16 bytes, as this is the minimum required by Eigen for any vectorisation.
  //
  // NOTE: It might be the case that we could get >= 16-byte alignment even if
  //       max_align_t < 16.  However we can't guarantee that this
  //       would happen (and it should not for any modern x86 machine) and if it
  //       didn't, we could get misaligned Jets.
  static constexpr int kAlignOrNot =
      // Work around a GCC 4.8 bug
      // (https://gcc.gnu.org/bugzilla/show_bug.cgi?id=56019) where
      // std::max_align_t is misplaced.
#if defined (__GNUC__) && __GNUC__ == 4 && __GNUC_MINOR__ == 8
      alignof(::max_align_t) >= 16
#else
      alignof(std::max_align_t) >= 16
#endif
      ? Eigen::AutoAlign : Eigen::DontAlign;

#if defined(EIGEN_MAX_ALIGN_BYTES)
  // Eigen >= 3.3 supports AVX & FMA instructions that require 32-byte alignment
  // (greater for AVX512).  Rather than duplicating the detection logic, use
  // Eigen's macro for the alignment size.
  //
  // NOTE: EIGEN_MAX_ALIGN_BYTES can be > 16 (e.g. 32 for AVX), even though
  //       kMaxAlignBytes will max out at 16.  We are therefore relying on
  //       Eigen's detection logic to ensure that this does not result in
  //       misaligned Jets.
#define CERES_JET_ALIGN_BYTES EIGEN_MAX_ALIGN_BYTES
#else
  // Eigen < 3.3 only supported 16-byte alignment.
#define CERES_JET_ALIGN_BYTES 16
#endif

  // Default to the native alignment if 16-byte alignment is not guaranteed to
  // be supported.  We cannot use alignof(T) as if we do, GCC 4.8 complains that
  // the alignment 'is not an integer constant', although Clang accepts it.
  static constexpr size_t kAlignment = kAlignOrNot == Eigen::AutoAlign
            ? CERES_JET_ALIGN_BYTES : alignof(double);

#undef CERES_JET_ALIGN_BYTES
  alignas(kAlignment) Eigen::Matrix<T, N, 1, kAlignOrNot> v;
#endif
};

// Unary +
template<typename T, int N> inline
Jet<T, N> const& operator+(const Jet<T, N>& f) {
  return f;
}

// TODO(keir): Try adding __attribute__((always_inline)) to these functions to
// see if it causes a performance increase.

// Unary -
template<typename T, int N> inline
Jet<T, N> operator-(const Jet<T, N>&f) {
  return Jet<T, N>(-f.a, -f.v);
}

// Binary +
template<typename T, int N> inline
Jet<T, N> operator+(const Jet<T, N>& f,
                    const Jet<T, N>& g) {
  return Jet<T, N>(f.a + g.a, f.v + g.v);
}

// Binary + with a scalar: x + s
template<typename T, int N> inline
Jet<T, N> operator+(const Jet<T, N>& f, T s) {
  return Jet<T, N>(f.a + s, f.v);
}

// Binary + with a scalar: s + x
template<typename T, int N> inline
Jet<T, N> operator+(T s, const Jet<T, N>& f) {
  return Jet<T, N>(f.a + s, f.v);
}

// Binary -
template<typename T, int N> inline
Jet<T, N> operator-(const Jet<T, N>& f,
                    const Jet<T, N>& g) {
  return Jet<T, N>(f.a - g.a, f.v - g.v);
}

// Binary - with a scalar: x - s
template<typename T, int N> inline
Jet<T, N> operator-(const Jet<T, N>& f, T s) {
  return Jet<T, N>(f.a - s, f.v);
}

// Binary - with a scalar: s - x
template<typename T, int N> inline
Jet<T, N> operator-(T s, const Jet<T, N>& f) {
  return Jet<T, N>(s - f.a, -f.v);
}

// Binary *
template<typename T, int N> inline
Jet<T, N> operator*(const Jet<T, N>& f,
                    const Jet<T, N>& g) {
  return Jet<T, N>(f.a * g.a, f.a * g.v + f.v * g.a);
}

// Binary * with a scalar: x * s
template<typename T, int N> inline
Jet<T, N> operator*(const Jet<T, N>& f, T s) {
  return Jet<T, N>(f.a * s, f.v * s);
}

// Binary * with a scalar: s * x
template<typename T, int N> inline
Jet<T, N> operator*(T s, const Jet<T, N>& f) {
  return Jet<T, N>(f.a * s, f.v * s);
}

// Binary /
template<typename T, int N> inline
Jet<T, N> operator/(const Jet<T, N>& f,
                    const Jet<T, N>& g) {
  // This uses:
  //
  //   a + u   (a + u)(b - v)   (a + u)(b - v)
  //   ----- = -------------- = --------------
  //   b + v   (b + v)(b - v)        b^2
  //
  // which holds because v*v = 0.
  const T g_a_inverse = T(1.0) / g.a;
  const T f_a_by_g_a = f.a * g_a_inverse;
  return Jet<T, N>(f_a_by_g_a, (f.v - f_a_by_g_a * g.v) * g_a_inverse);
}

// Binary / with a scalar: s / x
template<typename T, int N> inline
Jet<T, N> operator/(T s, const Jet<T, N>& g) {
  const T minus_s_g_a_inverse2 = -s / (g.a * g.a);
  return Jet<T, N>(s / g.a, g.v * minus_s_g_a_inverse2);
}

// Binary / with a scalar: x / s
template<typename T, int N> inline
Jet<T, N> operator/(const Jet<T, N>& f, T s) {
  const T s_inverse = T(1.0) / s;
  return Jet<T, N>(f.a * s_inverse, f.v * s_inverse);
}

// Binary comparison operators for both scalars and jets.
#define CERES_DEFINE_JET_COMPARISON_OPERATOR(op) 
template<typename T, int N> inline 
bool operator op(const Jet<T, N>& f, const Jet<T, N>& g) { 
  return f.a op g.a; 
} 
template<typename T, int N> inline 
bool operator op(const T& s, const Jet<T, N>& g) { 
  return s op g.a; 
} 
template<typename T, int N> inline 
bool operator op(const Jet<T, N>& f, const T& s) { 
  return f.a op s; 
}
CERES_DEFINE_JET_COMPARISON_OPERATOR( <  )  // NOLINT
CERES_DEFINE_JET_COMPARISON_OPERATOR( <= )  // NOLINT
CERES_DEFINE_JET_COMPARISON_OPERATOR( >  )  // NOLINT
CERES_DEFINE_JET_COMPARISON_OPERATOR( >= )  // NOLINT
CERES_DEFINE_JET_COMPARISON_OPERATOR( == )  // NOLINT
CERES_DEFINE_JET_COMPARISON_OPERATOR( != )  // NOLINT
#undef CERES_DEFINE_JET_COMPARISON_OPERATOR

// Pull some functions from namespace std.
//
// This is necessary because we want to use the same name (e.g. 'sqrt') for
// double-valued and Jet-valued functions, but we are not allowed to put
// Jet-valued functions inside namespace std.
using std::abs;
using std::acos;
using std::asin;
using std::atan;
using std::atan2;
using std::cbrt;
using std::ceil;
using std::cos;
using std::cosh;
using std::exp;
using std::exp2;
using std::floor;
using std::fmax;
using std::fmin;
using std::hypot;
using std::isfinite;
using std::isinf;
using std::isnan;
using std::isnormal;
using std::log;
using std::log2;
using std::pow;
using std::sin;
using std::sinh;
using std::sqrt;
using std::tan;
using std::tanh;

// Legacy names from pre-C++11 days.
inline bool IsFinite  (double x) { return std::isfinite(x); }
inline bool IsInfinite(double x) { return std::isinf(x);    }
inline bool IsNaN     (double x) { return std::isnan(x);    }
inline bool IsNormal  (double x) { return std::isnormal(x); }

// In general, f(a + h) ~= f(a) + f'(a) h, via the chain rule.

// abs(x + h) ~= x + h or -(x + h)
template <typename T, int N> inline
Jet<T, N> abs(const Jet<T, N>& f) {
  return f.a < T(0.0) ? -f : f;
}

// log(a + h) ~= log(a) + h / a
template <typename T, int N> inline
Jet<T, N> log(const Jet<T, N>& f) {
  const T a_inverse = T(1.0) / f.a;
  return Jet<T, N>(log(f.a), f.v * a_inverse);
}

// exp(a + h) ~= exp(a) + exp(a) h
template <typename T, int N> inline
Jet<T, N> exp(const Jet<T, N>& f) {
  const T tmp = exp(f.a);
  return Jet<T, N>(tmp, tmp * f.v);
}

// sqrt(a + h) ~= sqrt(a) + h / (2 sqrt(a))
template <typename T, int N> inline
Jet<T, N> sqrt(const Jet<T, N>& f) {
  const T tmp = sqrt(f.a);
  const T two_a_inverse = T(1.0) / (T(2.0) * tmp);
  return Jet<T, N>(tmp, f.v * two_a_inverse);
}

// cos(a + h) ~= cos(a) - sin(a) h
template <typename T, int N> inline
Jet<T, N> cos(const Jet<T, N>& f) {
  return Jet<T, N>(cos(f.a), - sin(f.a) * f.v);
}

// acos(a + h) ~= acos(a) - 1 / sqrt(1 - a^2) h
template <typename T, int N> inline
Jet<T, N> acos(const Jet<T, N>& f) {
  const T tmp = - T(1.0) / sqrt(T(1.0) - f.a * f.a);
  return Jet<T, N>(acos(f.a), tmp * f.v);
}

// sin(a + h) ~= sin(a) + cos(a) h
template <typename T, int N> inline
Jet<T, N> sin(const Jet<T, N>& f) {
  return Jet<T, N>(sin(f.a), cos(f.a) * f.v);
}

// asin(a + h) ~= asin(a) + 1 / sqrt(1 - a^2) h
template <typename T, int N> inline
Jet<T, N> asin(const Jet<T, N>& f) {
  const T tmp = T(1.0) / sqrt(T(1.0) - f.a * f.a);
  return Jet<T, N>(asin(f.a), tmp * f.v);
}

// tan(a + h) ~= tan(a) + (1 + tan(a)^2) h
template <typename T, int N> inline
Jet<T, N> tan(const Jet<T, N>& f) {
  const T tan_a = tan(f.a);
  const T tmp = T(1.0) + tan_a * tan_a;
  return Jet<T, N>(tan_a, tmp * f.v);
}

// atan(a + h) ~= atan(a) + 1 / (1 + a^2) h
template <typename T, int N> inline
Jet<T, N> atan(const Jet<T, N>& f) {
  const T tmp = T(1.0) / (T(1.0) + f.a * f.a);
  return Jet<T, N>(atan(f.a), tmp * f.v);
}

// sinh(a + h) ~= sinh(a) + cosh(a) h
template <typename T, int N> inline
Jet<T, N> sinh(const Jet<T, N>& f) {
  return Jet<T, N>(sinh(f.a), cosh(f.a) * f.v);
}

// cosh(a + h) ~= cosh(a) + sinh(a) h
template <typename T, int N> inline
Jet<T, N> cosh(const Jet<T, N>& f) {
  return Jet<T, N>(cosh(f.a), sinh(f.a) * f.v);
}

// tanh(a + h) ~= tanh(a) + (1 - tanh(a)^2) h
template <typename T, int N> inline
Jet<T, N> tanh(const Jet<T, N>& f) {
  const T tanh_a = tanh(f.a);
  const T tmp = T(1.0) - tanh_a * tanh_a;
  return Jet<T, N>(tanh_a, tmp * f.v);
}

// The floor function should be used with extreme care as this operation will
// result in a zero derivative which provides no information to the solver.
//
// floor(a + h) ~= floor(a) + 0
template <typename T, int N> inline
Jet<T, N> floor(const Jet<T, N>& f) {
  return Jet<T, N>(floor(f.a));
}

// The ceil function should be used with extreme care as this operation will
// result in a zero derivative which provides no information to the solver.
//
// ceil(a + h) ~= ceil(a) + 0
template <typename T, int N> inline
Jet<T, N> ceil(const Jet<T, N>& f) {
  return Jet<T, N>(ceil(f.a));
}

// Some new additions to C++11:

// cbrt(a + h) ~= cbrt(a) + h / (3 a ^ (2/3))
template <typename T, int N> inline
Jet<T, N> cbrt(const Jet<T, N>& f) {
  const T derivative = T(1.0) / (T(3.0) * cbrt(f.a * f.a));
  return Jet<T, N>(cbrt(f.a), f.v * derivative);
}

// exp2(x + h) = 2^(x+h) ~= 2^x + h*2^x*log(2)
template <typename T, int N> inline
Jet<T, N> exp2(const Jet<T, N>& f) {
  const T tmp = exp2(f.a);
  const T derivative = tmp * log(T(2));
  return Jet<T, N>(tmp, f.v * derivative);
}

// log2(x + h) ~= log2(x) + h / (x * log(2))
template <typename T, int N> inline
Jet<T, N> log2(const Jet<T, N>& f) {
  const T derivative = T(1.0) / (f.a * log(T(2)));
  return Jet<T, N>(log2(f.a), f.v * derivative);
}

// Like sqrt(x^2 + y^2),
// but acts to prevent underflow/overflow for small/large x/y.
// Note that the function is non-smooth at x=y=0,
// so the derivative is undefined there.
template <typename T, int N> inline
Jet<T, N> hypot(const Jet<T, N>& x, const Jet<T, N>& y) {
  // d/da sqrt(a) = 0.5 / sqrt(a)
  // d/dx x^2 + y^2 = 2x
  // So by the chain rule:
  // d/dx sqrt(x^2 + y^2) = 0.5 / sqrt(x^2 + y^2) * 2x = x / sqrt(x^2 + y^2)
  // d/dy sqrt(x^2 + y^2) = y / sqrt(x^2 + y^2)
  const T tmp = hypot(x.a, y.a);
  return Jet<T, N>(tmp, x.a / tmp * x.v + y.a / tmp * y.v);
}

template <typename T, int N> inline
const Jet<T, N>& fmax(const Jet<T, N>& x, const Jet<T, N>& y) {
  return x < y ? y : x;
}

template <typename T, int N> inline
const Jet<T, N>& fmin(const Jet<T, N>& x, const Jet<T, N>& y) {
  return y < x ? y : x;
}

// Bessel functions of the first kind with integer order equal to 0, 1, n.
//
// Microsoft has deprecated the j[0,1,n]() POSIX Bessel functions in favour of
// _j[0,1,n]().  Where available on MSVC, use _j[0,1,n]() to avoid deprecated
// function errors in client code (the specific warning is suppressed when
// Ceres itself is built).
inline double BesselJ0(double x) {
#if defined(CERES_MSVC_USE_UNDERSCORE_PREFIXED_BESSEL_FUNCTIONS)
  return _j0(x);
#else
  return j0(x);
#endif
}
inline double BesselJ1(double x) {
#if defined(CERES_MSVC_USE_UNDERSCORE_PREFIXED_BESSEL_FUNCTIONS)
  return _j1(x);
#else
  return j1(x);
#endif
}
inline double BesselJn(int n, double x) {
#if defined(CERES_MSVC_USE_UNDERSCORE_PREFIXED_BESSEL_FUNCTIONS)
  return _jn(n, x);
#else
  return jn(n, x);
#endif
}

// For the formulae of the derivatives of the Bessel functions see the book:
// Olver, Lozier, Boisvert, Clark, NIST Handbook of Mathematical Functions,
// Cambridge University Press 2010.
//
// Formulae are also available at http://dlmf.nist.gov

// See formula http://dlmf.nist.gov/10.6#E3
// j0(a + h) ~= j0(a) - j1(a) h
template <typename T, int N> inline
Jet<T, N> BesselJ0(const Jet<T, N>& f) {
  return Jet<T, N>(BesselJ0(f.a),
                   -BesselJ1(f.a) * f.v);
}

// See formula http://dlmf.nist.gov/10.6#E1
// j1(a + h) ~= j1(a) + 0.5 ( j0(a) - j2(a) ) h
template <typename T, int N> inline
Jet<T, N> BesselJ1(const Jet<T, N>& f) {
  return Jet<T, N>(BesselJ1(f.a),
                   T(0.5) * (BesselJ0(f.a) - BesselJn(2, f.a)) * f.v);
}

// See formula http://dlmf.nist.gov/10.6#E1
// j_n(a + h) ~= j_n(a) + 0.5 ( j_{n-1}(a) - j_{n+1}(a) ) h
template <typename T, int N> inline
Jet<T, N> BesselJn(int n, const Jet<T, N>& f) {
  return Jet<T, N>(BesselJn(n, f.a),
                   T(0.5) * (BesselJn(n - 1, f.a) - BesselJn(n + 1, f.a)) * f.v);
}

// Jet Classification. It is not clear what the appropriate semantics are for
// these classifications. This picks that std::isfinite and std::isnormal are "all"
// operations, i.e. all elements of the jet must be finite for the jet itself
// to be finite (or normal). For IsNaN and IsInfinite, the answer is less
// clear. This takes a "any" approach for IsNaN and IsInfinite such that if any
// part of a jet is nan or inf, then the entire jet is nan or inf. This leads
// to strange situations like a jet can be both IsInfinite and IsNaN, but in
// practice the "any" semantics are the most useful for e.g. checking that
// derivatives are sane.

// The jet is finite if all parts of the jet are finite.
template <typename T, int N> inline
bool isfinite(const Jet<T, N>& f) {
  if (!std::isfinite(f.a)) {
    return false;
  }
  for (int i = 0; i < N; ++i) {
    if (!std::isfinite(f.v[i])) {
      return false;
    }
  }
  return true;
}

// The jet is infinite if any part of the Jet is infinite.
template <typename T, int N> inline
bool isinf(const Jet<T, N>& f) {
  if (std::isinf(f.a)) {
    return true;
  }
  for (int i = 0; i < N; ++i) {
    if (std::isinf(f.v[i])) {
      return true;
    }
  }
  return false;
}


// The jet is NaN if any part of the jet is NaN.
template <typename T, int N> inline
bool isnan(const Jet<T, N>& f) {
  if (std::isnan(f.a)) {
    return true;
  }
  for (int i = 0; i < N; ++i) {
    if (std::isnan(f.v[i])) {
      return true;
    }
  }
  return false;
}

// The jet is normal if all parts of the jet are normal.
template <typename T, int N> inline
bool isnormal(const Jet<T, N>& f) {
  if (!std::isnormal(f.a)) {
    return false;
  }
  for (int i = 0; i < N; ++i) {
    if (!std::isnormal(f.v[i])) {
      return false;
    }
  }
  return true;
}

// Legacy functions from the pre-C++11 days.
template <typename T, int N>
inline bool IsFinite(const Jet<T, N>& f) {
  return isfinite(f);
}

template <typename T, int N>
inline bool IsNaN(const Jet<T, N>& f) {
  return isnan(f);
}

template <typename T, int N>
inline bool IsNormal(const Jet<T, N>& f) {
  return isnormal(f);
}

// The jet is infinite if any part of the jet is infinite.
template <typename T, int N> inline
bool IsInfinite(const Jet<T, N>& f) {
  return isinf(f);
}

// atan2(b + db, a + da) ~= atan2(b, a) + (- b da + a db) / (a^2 + b^2)
//
// In words: the rate of change of theta is 1/r times the rate of
// change of (x, y) in the positive angular direction.
template <typename T, int N> inline
Jet<T, N> atan2(const Jet<T, N>& g, const Jet<T, N>& f) {
  // Note order of arguments:
  //
  //   f = a + da
  //   g = b + db

  T const tmp = T(1.0) / (f.a * f.a + g.a * g.a);
  return Jet<T, N>(atan2(g.a, f.a), tmp * (- g.a * f.v + f.a * g.v));
}


// pow -- base is a differentiable function, exponent is a constant.
// (a+da)^p ~= a^p + p*a^(p-1) da
template <typename T, int N> inline
Jet<T, N> pow(const Jet<T, N>& f, double g) {
  T const tmp = g * pow(f.a, g - T(1.0));
  return Jet<T, N>(pow(f.a, g), tmp * f.v);
}

// pow -- base is a constant, exponent is a differentiable function.
// We have various special cases, see the comment for pow(Jet, Jet) for
// analysis:
//
// 1. For f > 0 we have: (f)^(g + dg) ~= f^g + f^g log(f) dg
//
// 2. For f == 0 and g > 0 we have: (f)^(g + dg) ~= f^g
//
// 3. For f < 0 and integer g we have: (f)^(g + dg) ~= f^g but if dg
// != 0, the derivatives are not defined and we return NaN.

template <typename T, int N> inline
Jet<T, N> pow(double f, const Jet<T, N>& g) {
  if (f == 0 && g.a > 0) {
    // Handle case 2.
    return Jet<T, N>(T(0.0));
  }
  if (f < 0 && g.a == floor(g.a)) {
    // Handle case 3.
    Jet<T, N> ret(pow(f, g.a));
    for (int i = 0; i < N; i++) {
      if (g.v[i] != T(0.0)) {
        // Return a NaN when g.v != 0.
        ret.v[i] = std::numeric_limits<T>::quiet_NaN();
      }
    }
    return ret;
  }
  // Handle case 1.
  T const tmp = pow(f, g.a);
  return Jet<T, N>(tmp, log(f) * tmp * g.v);
}

// pow -- both base and exponent are differentiable functions. This has a
// variety of special cases that require careful handling.
//
// 1. For f > 0:
//    (f + df)^(g + dg) ~= f^g + f^(g - 1) * (g * df + f * log(f) * dg)
//    The numerical evaluation of f * log(f) for f > 0 is well behaved, even for
//    extremely small values (e.g. 1e-99).
//
// 2. For f == 0 and g > 1: (f + df)^(g + dg) ~= 0
//    This cases is needed because log(0) can not be evaluated in the f > 0
//    expression. However the function f*log(f) is well behaved around f == 0
//    and its limit as f-->0 is zero.
//
// 3. For f == 0 and g == 1: (f + df)^(g + dg) ~= 0 + df
//
// 4. For f == 0 and 0 < g < 1: The value is finite but the derivatives are not.
//
// 5. For f == 0 and g < 0: The value and derivatives of f^g are not finite.
//
// 6. For f == 0 and g == 0: The C standard incorrectly defines 0^0 to be 1
//    "because there are applications that can exploit this definition". We
//    (arbitrarily) decree that derivatives here will be nonfinite, since that
//    is consistent with the behavior for f == 0, g < 0 and 0 < g < 1.
//    Practically any definition could have been justified because mathematical
//    consistency has been lost at this point.
//
// 7. For f < 0, g integer, dg == 0: (f + df)^(g + dg) ~= f^g + g * f^(g - 1) df
//    This is equivalent to the case where f is a differentiable function and g
//    is a constant (to first order).
//
// 8. For f < 0, g integer, dg != 0: The value is finite but the derivatives are
//    not, because any change in the value of g moves us away from the point
//    with a real-valued answer into the region with complex-valued answers.
//
// 9. For f < 0, g noninteger: The value and derivatives of f^g are not finite.

template <typename T, int N> inline
Jet<T, N> pow(const Jet<T, N>& f, const Jet<T, N>& g) {
  if (f.a == 0 && g.a >= 1) {
    // Handle cases 2 and 3.
    if (g.a > 1) {
      return Jet<T, N>(T(0.0));
    }
    return f;
  }
  if (f.a < 0 && g.a == floor(g.a)) {
    // Handle cases 7 and 8.
    T const tmp = g.a * pow(f.a, g.a - T(1.0));
    Jet<T, N> ret(pow(f.a, g.a), tmp * f.v);
    for (int i = 0; i < N; i++) {
      if (g.v[i] != T(0.0)) {
        // Return a NaN when g.v != 0.
        ret.v[i] = std::numeric_limits<T>::quiet_NaN();
      }
    }
    return ret;
  }
  // Handle the remaining cases. For cases 4,5,6,9 we allow the log() function
  // to generate -HUGE_VAL or NaN, since those cases result in a nonfinite
  // derivative.
  T const tmp1 = pow(f.a, g.a);
  T const tmp2 = g.a * pow(f.a, g.a - T(1.0));
  T const tmp3 = tmp1 * log(f.a);
  return Jet<T, N>(tmp1, tmp2 * f.v + tmp3 * g.v);
}

// Note: This has to be in the ceres namespace for argument dependent lookup to
// function correctly. Otherwise statements like CHECK_LE(x, 2.0) fail with
// strange compile errors.
template <typename T, int N>
inline std::ostream &operator<<(std::ostream &s, const Jet<T, N>& z) {
  s << "[" << z.a << " ; ";
  for (int i = 0; i < N; ++i) {
    s << z.v[i];
    if (i != N - 1) {
      s << ", ";
    }
  }
  s << "]";
  return s;
}

}  // namespace ceres

namespace Eigen {

// Creating a specialization of NumTraits enables placing Jet objects inside
// Eigen arrays, getting all the goodness of Eigen combined with autodiff.
template<typename T, int N>
struct NumTraits<ceres::Jet<T, N>> {
  typedef ceres::Jet<T, N> Real;
  typedef ceres::Jet<T, N> NonInteger;
  typedef ceres::Jet<T, N> Nested;
  typedef ceres::Jet<T, N> Literal;

  static typename ceres::Jet<T, N> dummy_precision() {
    return ceres::Jet<T, N>(1e-12);
  }

  static inline Real epsilon() {
    return Real(std::numeric_limits<T>::epsilon());
  }

  static inline int digits10() { return NumTraits<T>::digits10(); }

  enum {
    IsComplex = 0,
    IsInteger = 0,
    IsSigned,
    ReadCost = 1,
    AddCost = 1,
    // For Jet types, multiplication is more expensive than addition.
    MulCost = 3,
    HasFloatingPoint = 1,
    RequireInitialization = 1
  };

  template<bool Vectorized>
  struct Div {
    enum {
#if defined(EIGEN_VECTORIZE_AVX)
      AVX = true,
#else
      AVX = false,
#endif

      // Assuming that for Jets, division is as expensive as
      // multiplication.
      Cost = 3
    };
  };

  static inline Real highest() { return Real(std::numeric_limits<T>::max()); }
  static inline Real lowest() { return Real(-std::numeric_limits<T>::max()); }
};

#if EIGEN_VERSION_AT_LEAST(3, 3, 0)
// Specifying the return type of binary operations between Jets and scalar types
// allows you to perform matrix/array operations with Eigen matrices and arrays
// such as addition, subtraction, multiplication, and division where one Eigen
// matrix/array is of type Jet and the other is a scalar type. This improves
// performance by using the optimized scalar-to-Jet binary operations but
// is only available on Eigen versions >= 3.3
template <typename BinaryOp, typename T, int N>
struct ScalarBinaryOpTraits<ceres::Jet<T, N>, T, BinaryOp> {
  typedef ceres::Jet<T, N> ReturnType;
};
template <typename BinaryOp, typename T, int N>
struct ScalarBinaryOpTraits<T, ceres::Jet<T, N>, BinaryOp> {
  typedef ceres::Jet<T, N> ReturnType;
};
#endif  // EIGEN_VERSION_AT_LEAST(3, 3, 0)

}  // namespace Eigen

#endif  // CERES_PUBLIC_JET_H_

 Modeling Non-linear Least Squares

 CostFunction

• CostFunction

is responsible for computing a vector of residules and Jacobian matrices.

• SizedCostFunction

SizedCostFunction继承自CostFunction,can be used if the size of parameter blocks and the size of residual vector is known at compile time(this is the common case).

• AutoDiffCostFunction

AutoDiffCostFunction继承自SizedCostFunction，要求参数块数目以及每个参数块大小在编译时已知，要求参数块数目不超过10个。can compute derivatives automaticlly.To get an auto differentiated cost function, you must define a class with a templated operator()(a functor) that computes the cost function in terms of the template parameter T. The autodiff framework substitutes appropriate Jet objects for T in order to compute the derivative when necessary, but this is hidden, and you should write the function as if T were a scalar type (e.g. a double-precision floating point number).

• DynamicAutoDiffCostFunction

can be used when the number of parameter blocks and their sizes not known at compile time.

• NumericDiffCostFunction

can be used when the evaluation of the residual involves a call to library function that you do not have control over.

• ConditionedCostFunction

allows to apply different conditioning to the residual values of a wrapped cost function.

LossFunction

 LossFunction reduces the influence of outliers, this leads to outlier terms getting downweighted so they do not overly influence the final solution.

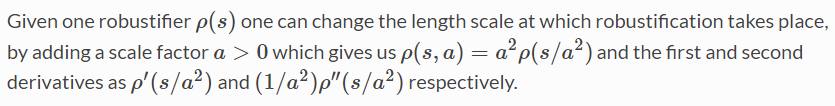
LocalParameterization

 Trust Region 信赖域

Trust region methods are in some sense dual to line search methods:trust region methods first choose a step size(the size of trust region) and then a step direction while line search methods first choose a step direction and then a step size.

 Levenberg-Marquardt

Dogleg

Line Search Methods

The line search method in Ceres Solver cannot handle bounds constraints right now, so it can only be used for solving unconstrained problems.