强连通分量
(Tarjan)
强连通分量是神马东东?就是有向图中一群能相互到达的点。比如说这么一个图:
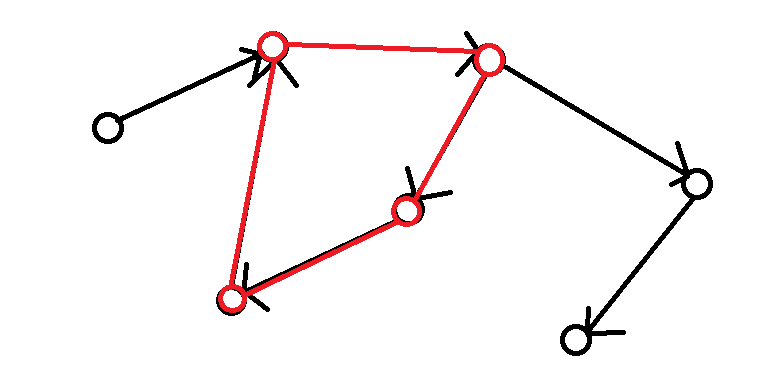
中间那个红色的就是强连通分量。
在很多题中,一个强连通分量可以看做一个点,但若直接跑最短路的话,成环显然不好处理,所以要先预处理将他们看成一个点。这是稍后的缩点。这里先讲怎么求强联通分量。
我们记录一个(dfs)序,表示每个点被搜到的顺序。再记录一个(low)表示这个点能到达的最早被搜过的点是哪个。
每搜到一个点就让他入栈。
显然,在我们还没有搜到能往已经被搜到的点连线的点时,所有搜过的点是一棵树。当我们搜到能往已经被搜到的点连线的点时,说明我们找到了一条在树上的后向边。如图。
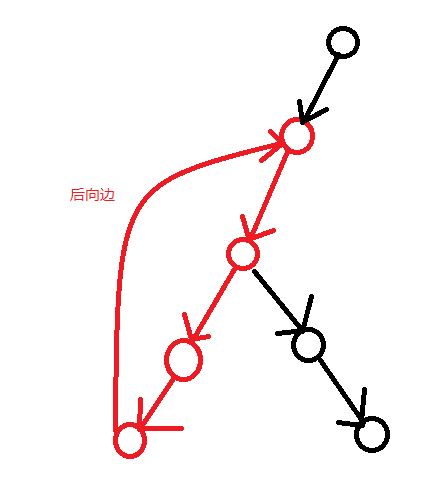
当我们递归搜到这么一条边的时候,发现它的儿子节点已经被搜过了,我们就记录一下,它最早能搜到的点是谁。
当我们回溯的时候,判断一下当前节点的(dfn)值与(low)记录的值是否相同。若相同,则说明它是这个强联通分量里最早被搜到的点,我们就让这些点出栈。显然,在这个点上面的点(指在栈中的位置)全部是这个强连通分量里的点。因为当前点是这个强连通分量里最早被搜到的,必然最早入栈;而其他强连通分量里的点已经出栈了。我们只要从栈顶出栈,一直到这个点就好了。这些点就是属于一个强连通分量里的点。
细节看代码。
#include <iostream>
#include <cstdio>
using namespace std;
inline long long read() {
long long x = 0; int f = 0; char c = getchar();
while (c < '0' || c > '9') f |= c == '-', c = getchar();
while (c >= '0' && c <= '9') x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
return f? -x:x;
}
int n, m, hd[10005], cnt, w[10005], dfn[10005], low[10005], s[10005], top;
int f[10005], out[10005];
struct szh {
int y, nxt, x;
}a[50005];
inline void add(int x, int y) {
a[++cnt].y = y, a[cnt].nxt = hd[x], hd[x] = cnt, a[cnt].x = x;
}
bool vis[10005];
int num;
inline void Tarjan(int u) {//u表示当前点
dfn[u] = ++cnt; low[u] = cnt; vis[u] = 1; s[++top] = u;
for (int i = hd[u], v; v = a[i].y, i; i = a[i].nxt)
if (!dfn[v]) {/如果这个点没有搜到过,就去搜索
Tarjan(v);
low[u] = min(low[u], low[v]);//回来的时候更新
}
//若这个点被搜过,且它还在栈里,我们就用它的dfn值去更新。因为这个点不一定搜完了,而且它一定不是别的强连通分量里的。
else if (vis[v]) low[u] = min(low[u], dfn[v]);
if (dfn[u] == low[u]) {//若当前点是这个强连通分量里最早被搜到的点,就退栈,记录答案
vis[u] = 0; f[u] = ++num; w[num] = 1;
int k = s[top--];
while (k != u && top) {
w[num]++; f[k] = num;
k = s[top--];
}
}
}
int main() {
n = read(); m = read();
for (int i = 1; i <= m; ++i) {
int x = read(), y = read();
add(x, y);
}
cnt = 0;
for (int i = 1; i <= n; ++i)
if (!dfn[i]) Tarjan(i);//因为图不一定联通
for (int i = 1; i <= m; ++i)
if (f[a[i].y] != f[a[i].x]) out[f[a[i].x]]++;
int k = 0, ans = 0;
for (int i = 1; i <= num; ++i)
if (!out[i]) k = i, ans++;
printf("%d
", ans > 1? 0 : w[k]);
return 0;
}
欢迎指正评论O(∩_∩)O~~