# -*- coding: utf-8 -*-
# @Time:
# @Auther: kongweixin
# @File:
""""""
"""
一:递归的定义和调用
递归调用:是函数嵌套调用的一种特殊形式具体是指:
在调用一个函数的过程中又直接或者间接地调用到本身
#直接调用本身:在调用f1的过程中,又调用f1,这就是直接调用函数f1本身
def f1():
print('是我是我还是我')
f1()
f1()
# 间接接调用本身:在调用f1的过程中,又调用f2,而在调用f2的过程中又调用f1,这就是间接调用函数f1本身
def f1():
print('===>f1')
f2()
def f2():
print('===>f2')
f1()
f1()
两种情况下的递归调用都是一个无限循环的过程,但在python对函数的递归调用的深度做了限制,
因而并不会像大家所想的那样进入无限循环,会抛出异常,要避免出现这种情况,就必须让递归调用在满足某个特定条件下终止。
# 一段代码的循环运行的方案有两种
# 方式一:while、for循环
while True:
print(1111)
print(2222)
print(3333)
# 方式二:递归的本质就是循环:
def f1():
print(1111)
print(2222)
print(3333)
f1()
f1()
二:需要强调的的一点是:
# 递归调用不应该无限地调用下去,必须在满足某种条件下结束递归调用
n=0
while n < 10:
print(n)
n+=1
def f1(n):
if n == 10:
return
print(n)
n+=1
f1(n)
f1(0)
!!!!提示!!!!
#1. 可以使用sys.getrecursionlimit()去查看递归深度,默认值为1000,虽然可以使用
sys.setrecursionlimit()去设定该值,但仍受限于主机操作系统栈大小的限制
#2. python不是一门函数式编程语言,无法对递归进行尾递归优化。
三:递归的两个阶段
# 回溯:一层一层调用下去
# 递推:满足某种结束条件,结束递归调用,然后一层一层返回
下面我们用一个浅显的例子,为了让读者阐释递归的原理和使用:
例4.5
某公司四个员工坐在一起,问第四个人薪水,他说比第三个人多1000,
问第三个人薪水,第他说比第二个人多1000,问第二个人薪水,他说比第一个人多1000,
最后第一人说自己每月5000,请问第四个人的薪水是多少?
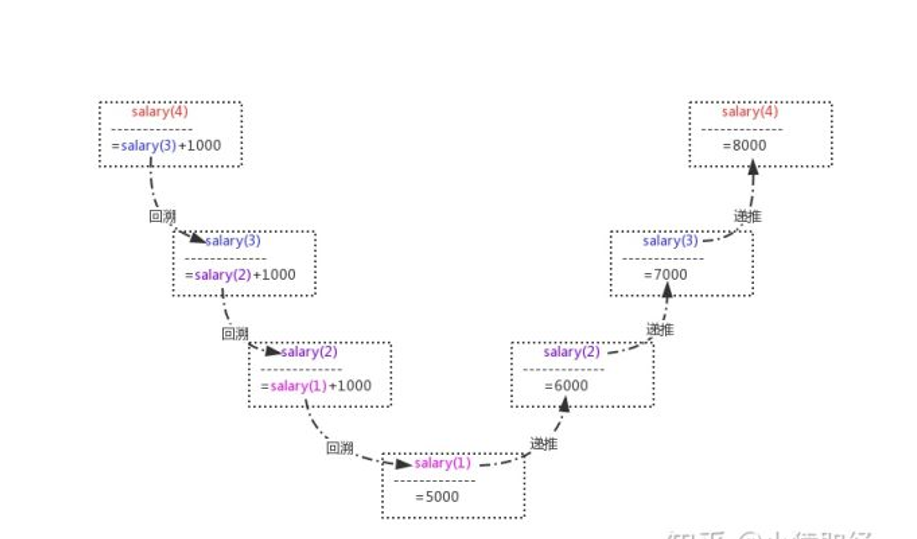
思路解析:
要知道第四个人的月薪,就必须知道第三个人的,第三个人的又取决于第二个人的,
第二个人的又取决于第一个人的,而且每一个员工都比前一个多一千,
数学表达式即:
salary(4)=salary(3)+1000
salary(3)=salary(2)+1000
salary(2)=salary(1)+1000
salary(1)=5000
总结为:
salary(n)=salary(n-1)+1000 (n>1)
salary(1)=5000 (n=1)
可以将该过程分为两个阶段:回溯和递推。
在回溯阶段,要求第n个员工的薪水,需要回溯得到(n-1)个员工的薪水,以此类推,
直到得到第一个员工的薪水,此时,salary(1)已知,因而不必再向前回溯了。然后进入递推阶段:
从第一个员工的薪水可以推算出第二个员工的薪水(6000),从第二个员工的薪水可以推算出第三个员工的薪水(7000),
以此类推,一直推算出第第四个员工的薪水(8000)为止,递归结束。需要注意的一点是,递归一定要有一个结束条件,
这里n=1就是结束条件。
def salary(n):
if n==1:
return 5000
return salary(n-1)+1000
s=salary(4)
print(s)
程序分析:
在未满足n==1的条件时,一直进行递归调用,即一直回溯,见图的左半部分。而在满足n==1的条件时,终止递归调用,
即结束回溯,从而进入递推阶段,依次推导直到得到最终的结果。
递归本质就是在做重复的事情,所以理论上递归可以解决的问题循环也都可以解决,只不过在某些情况下,使用递归会更容易实现,
比如有一个嵌套多层的列表,要求打印出所有的元素,,代码实现如下:
递归的应用
示例1:
l=[1,2,[3,[4]]]
def f1(list1):
for x in list1:
if type(x) is list:
# 如果是列表,应该再循环、再判断,即重新运行本身的代码
f1(x)
else:
print(x)
f1(l)
示例2:
items=[[1,2],3,[4,[5,[6,7]]]]
def foo(items):
for i in items:
if isinstance(i,list): #满足未遍历完items以及if判断成立的条件时,一直进行递归调用
foo(i)
else:
print(i,end=' ')
foo(items) #打印结果1 2 3 4 5 6 7
使用递归,我们只需要分析出要重复执行的代码逻辑,然后提取进入下一次递归调用的条件或者说递归结束的条件即可,代码实现起来简洁清晰
"""
