数据结构学习笔记04树(堆哈夫曼树并查集)

一.堆(heap)

优先队列（Priority Queue）：特殊的“队列”，取出元素的顺序是依照元素的优先权（关键字）大小，而不是元素进入队列的先后顺序。

数组 :
插入 — 元素总是插入尾部 ~ O ( 1 )
删除 — 查找最大（或最小）关键字 ~ O ( n )
从数组中删去需要移动元素 ~ O( n )
链表:
插入 — 元素总是插入链表的头部 ~ O ( 1 )
删除 — 查找最大（或最小）关键字 ~ O ( n )
删去结点 ~ O( 1 )
有序数组:
插入 — 找到合适的位置 ~ O( n ) 或 O(log2 n )
移动元素并插入 ~ O( n )
删除 — 删去最后一个元素 ~ O( 1 )
有序链表:
插入 — 找到合适的位置 ~ O( n )
插入元素 ~ O( 1 )
删除 — 删除首元素或最后元素 ~ O( 1 )
二叉树
    删除会导致不平衡

若采用数组或链表实现优先队列

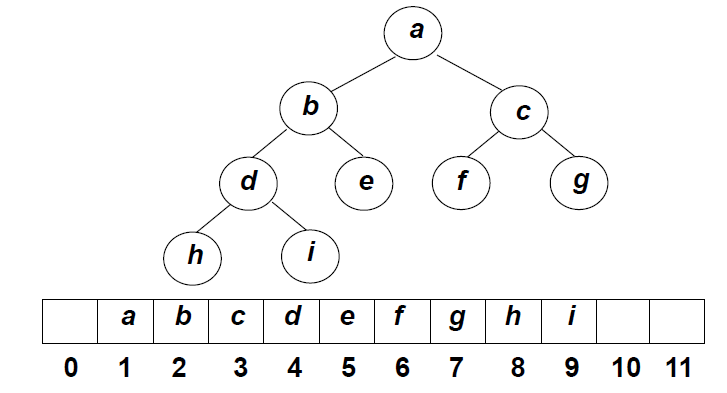
优先队列的完全二叉树表示

堆的两个特性

　　结构性：用数组表示的完全二叉树；

　　有序性：任一结点的关键字是其子树所有结点的最大值(或最小值)

　　　　“最大堆(MaxHeap)”,也称“大顶堆”：最大值

　　　　 “最小堆(MinHeap)”,也称“小顶堆” ：最小值

1.最大堆(代码：sj4_3)

  1 //最大堆 
  2 #include <stdio.h>
  3 #include <stdlib.h>
  4 
  5 #define MAXDATA 1000  /* 该值应根据具体情况定义为大于堆中所有可能元素的值 */
  6 #define ERROR -1 /* 错误标识应根据具体情况定义为堆中不可能出现的元素值 */
  7 
  8 typedef int ElementType;
  9 
 10 typedef struct HNode *Heap; /* 堆的类型定义 */
 11 struct HNode {
 12     ElementType *Data; /* 存储元素的数组 */
 13     int Size;          /* 堆中当前元素个数 */
 14     int Capacity;      /* 堆的最大容量 */
 15 };
 16 typedef Heap MaxHeap; /* 最大堆 */
 17  
 18 MaxHeap CreateHeap( int MaxSize );
 19 bool IsFull( MaxHeap H );
 20 bool Insert( MaxHeap H, ElementType X );
 21 bool IsEmpty( MaxHeap H );
 22 ElementType DeleteMax( MaxHeap H );
 23 void PercDown( MaxHeap H, int p );
 24 void BuildHeap( MaxHeap H );
 25 
 26 int main()
 27 {
 28     MaxHeap Heap;
 29     Heap = CreateHeap( 10 );
 30     BuildHeap(Heap);
 31     Insert( Heap, 1);
 32     Insert( Heap, 2);
 33     Insert( Heap, 3);
 34     ElementType Max = DeleteMax( Heap );
 35     printf("%d
",Max);
 36     return 0;    
 37 } 
 38 
 39 /* 创建容量为MaxSize的空的最大堆 */ 
 40 MaxHeap CreateHeap( int MaxSize )
 41 { 
 42  
 43     MaxHeap H = (MaxHeap)malloc(sizeof(struct HNode));
 44     H->Data = (ElementType *)malloc((MaxSize+1)*sizeof(ElementType));
 45     H->Size = 0;
 46     H->Capacity = MaxSize;
 47     H->Data[0] = MAXDATA; /* 定义"哨兵"为大于堆中所有可能元素的值*/
 48  
 49     return H;
 50 }
 51  
 52 bool IsFull( MaxHeap H )
 53 {
 54     return (H->Size == H->Capacity);
 55 }
 56 
 57 /* 将元素X插入最大堆H，其中H->Data[0]已经定义为哨兵 */ 
 58 bool Insert( MaxHeap H, ElementType X )
 59 {
 60     if ( IsFull(H) ) { 
 61         printf("最大堆已满");
 62         return false;
 63     }
 64     int i = ++H->Size; /* i指向插入后堆中的最后一个元素的位置 */
 65     for ( ; H->Data[i/2] < X; i /= 2 )
 66         H->Data[i] = H->Data[i/2]; /* 上滤X */
 67     H->Data[i] = X; /* 将X插入 */
 68     return true;
 69 }
 70 
 71 bool IsEmpty( MaxHeap H )
 72 {
 73     return (H->Size == 0);
 74 }
 75 
 76 /* 从最大堆H中取出键值为最大的元素，并删除一个结点 */ 
 77 ElementType DeleteMax( MaxHeap H )
 78 { 
 79     int Parent, Child;
 80     ElementType MaxItem, X;
 81  
 82     if ( IsEmpty(H) ) {
 83         printf("最大堆已为空");
 84         return ERROR;
 85     }
 86  
 87     MaxItem = H->Data[1]; /* 取出根结点存放的最大值 */
 88     /* 用最大堆中最后一个元素从根结点开始向上过滤下层结点 */
 89     X = H->Data[H->Size--]; /* 注意当前堆的规模要减小 */
 90     for( Parent = 1; Parent * 2 <= H->Size; Parent = Child ) {
 91         Child = Parent * 2;
 92         if( (Child != H->Size) && (H->Data[Child] < H->Data[Child+1]) )
 93             Child++;  /* Child指向左右子结点的较大者 */
 94         if( X >= H->Data[Child] ) break; /* 找到了合适位置 */
 95         else  /* 下滤X */
 96             H->Data[Parent] = H->Data[Child];
 97     }
 98     H->Data[Parent] = X;
 99  
100     return MaxItem;
101 } 
102  
103 /*----------- 建造最大堆 -----------*/
104 /* 下滤：将H中以H->Data[p]为根的子堆调整为最大堆 */
105 void PercDown( MaxHeap H, int p )
106 {
107     int Parent, Child;
108     ElementType X;
109  
110     X = H->Data[p]; /* 取出根结点存放的值 */
111     for( Parent = p; Parent*2 <= H->Size; Parent = Child ) {
112         Child = Parent * 2;
113         if( (Child != H->Size) && (H->Data[Child] < H->Data[Child+1]) )
114             Child++;  /* Child指向左右子结点的较大者 */
115         if( X >= H->Data[Child] ) break; /* 找到了合适位置 */
116         else  /* 下滤X */
117             H->Data[Parent] = H->Data[Child];
118     }
119     H->Data[Parent] = X;
120 }
121 
122 /* 调整H->Data[]中的元素，使满足最大堆的有序性  */
123 /* 这里假设所有H->Size个元素已经存在H->Data[]中 */
124 void BuildHeap( MaxHeap H )
125 {
126     /* 从最后一个结点的父节点开始，到根结点1 */
127     for(int i = H->Size/2; i > 0; i-- )
128         PercDown( H, i );
129 }

sj4_3

typedef struct HNode *Heap; /* 堆的类型定义 */
struct HNode {
　　ElementType *Data; /* 存储元素的数组 */
　　int Size; /* 堆中当前元素个数 */
　　int Capacity; /* 堆的最大容量 */
};
typedef Heap MaxHeap; /* 最大堆 */

1.创建最大堆

/* 创建容量为MaxSize的空的最大堆 */ 
MaxHeap CreateHeap( int MaxSize )
{ 
 
    MaxHeap H = (MaxHeap)malloc(sizeof(struct HNode));
    H->Data = (ElementType *)malloc((MaxSize+1)*sizeof(ElementType));
    H->Size = 0;
    H->Capacity = MaxSize;
    H->Data[0] = MAXDATA; /* 定义"哨兵"为大于堆中所有可能元素的值*/
 
    return H;
}

View Code

2.最大堆的插入

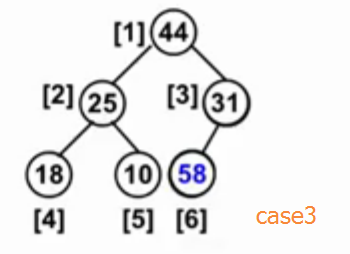
将新插入的元素放在数组的最后位置。

　　case1：新插入元素小于其parent。例如插入20，未破坏其有序性，插入成功。

　　case2：新插入元素大于其parent。例如插入35，破坏其结点是其子树所有结点的最大值，交换35与其parent31位置。

　　case3：新插入元素大于其parent的parent……。例如插入58，若其大于parent，交换，一直往上换。

 1 /* 将元素X插入最大堆H，其中H->Data[0]已经定义为哨兵 */ 
 2 bool Insert( MaxHeap H, ElementType X )
 3 {
 4     if ( IsFull(H) ) { 
 5         printf("最大堆已满");
 6         return false;
 7     }
 8     int i = ++H->Size; /* i指向插入后堆中的最后一个元素的位置 */
 9     for ( ; H->Data[i/2] < X; i /= 2 )
10         H->Data[i] = H->Data[i/2]; /* 上滤X */
11     H->Data[i] = X; /* 将X插入 */
12     return true;
13 }

View Code

3.最大堆的删除

获取根(即最大值)，删除最后的结点，放入根位置。取根最大的孩子与根交换，最大孩子的最大孩子与其交换，一直向下换。

 1 /* 从最大堆H中取出键值为最大的元素，并删除一个结点 */ 
 2 ElementType DeleteMax( MaxHeap H )
 3 { 
 4     int Parent, Child;
 5     ElementType MaxItem, X;
 6  
 7     if ( IsEmpty(H) ) {
 8         printf("最大堆已为空");
 9         return ERROR;
10     }
11  
12     MaxItem = H->Data[1]; /* 取出根结点存放的最大值 */
13     /* 用最大堆中最后一个元素从根结点开始向上过滤下层结点 */
14     X = H->Data[H->Size--]; /* 注意当前堆的规模要减小 */
15     for( Parent = 1; Parent * 2 <= H->Size; Parent = Child ) {
16         Child = Parent * 2;
17         if( (Child != H->Size) && (H->Data[Child] < H->Data[Child+1]) )
18             Child++;  /* Child指向左右子结点的较大者 */
19         if( X >= H->Data[Child] ) break; /* 找到了合适位置 */
20         else  /* 下滤X */
21             H->Data[Parent] = H->Data[Child];
22     }
23     H->Data[Parent] = X;
24  
25     return MaxItem;
26 }

View Code

4.最大堆的建立：将已经存在的N个元素按最大堆的要求存放在一个一维数组中

　　方法1：通过插入操作，将N个元素一个个相继插入到一个初始为空的堆中去，其时间代价最大为O(N logN)。　　　　

　　方法2：在线性时间复杂度下建立最大堆。
　　　　①将N个元素按输入顺序存入，先满足完全二叉树的结构特性
　　　　②调整各结点位置，以满足最大堆的有序特性。

从最小单位堆开始建堆，从后往前，第一个有孩子的最小单位堆开始。

 1 /*----------- 建造最大堆 -----------*/
 2 /* 下滤：将H中以H->Data[p]为根的子堆调整为最大堆 */
 3 void PercDown( MaxHeap H, int p )
 4 {
 5     int Parent, Child;
 6     ElementType X;
 7  
 8     X = H->Data[p]; /* 取出根结点存放的值 */
 9     for( Parent = p; Parent*2 <= H->Size; Parent = Child ) {
10         Child = Parent * 2;
11         if( (Child != H->Size) && (H->Data[Child] < H->Data[Child+1]) )
12             Child++;  /* Child指向左右子结点的较大者 */
13         if( X >= H->Data[Child] ) break; /* 找到了合适位置 */
14         else  /* 下滤X */
15             H->Data[Parent] = H->Data[Child];
16     }
17     H->Data[Parent] = X;
18 }
19 
20 /* 调整H->Data[]中的元素，使满足最大堆的有序性  */
21 /* 这里假设所有H->Size个元素已经存在H->Data[]中 */
22 void BuildHeap( MaxHeap H )
23 {
24     /* 从最后一个结点的父节点开始，到根结点1 */
25     for(int i = H->Size/2; i > 0; i-- )
26         PercDown( H, i );
27 }

View Code

2.最小堆(代码：sj4_4)

同理

  1 //最小堆 
  2 #include <stdio.h>
  3 #include <stdlib.h>
  4 
  5 #define MINDATA -1000  /* 该值应根据具体情况定义为小于堆中所有可能元素的值 */
  6 #define ERROR -1 /* 错误标识应根据具体情况定义为堆中不可能出现的元素值 */
  7 
  8 typedef int ElementType;
  9 
 10 typedef struct HNode *Heap; /* 堆的类型定义 */
 11 struct HNode {
 12     ElementType *Data; /* 存储元素的数组 */
 13     int Size;          /* 堆中当前元素个数 */
 14     int Capacity;      /* 堆的最大容量 */
 15 };
 16 typedef Heap MinHeap; /* 最小堆 */
 17 
 18 MinHeap CreateHeap( int MaxSize );
 19 bool IsFull( MinHeap H );
 20 bool Insert( MinHeap H, ElementType X );
 21 bool IsEmpty( MinHeap H );
 22 ElementType DeleteMin( MinHeap H );
 23 void PercDown( MinHeap H, int p );
 24 void BuildHeap( MinHeap H );
 25 
 26 int main()
 27 {
 28     MinHeap Heap;
 29     Heap = CreateHeap( 10 );
 30     BuildHeap(Heap);
 31     Insert( Heap, 1);
 32     Insert( Heap, 2);
 33     Insert( Heap, 3);
 34     Insert( Heap, 4);
 35     ElementType Min = DeleteMin( Heap );
 36     printf("%d
",Min);
 37     Min = DeleteMin( Heap );
 38     printf("%d
",Min);
 39     Min = DeleteMin( Heap );
 40     printf("%d
",Min);
 41     return 0;    
 42 } 
 43 
 44 /* 创建容量为MaxSize的空的最小堆 */ 
 45 MinHeap CreateHeap( int MaxSize )
 46 { 
 47  
 48     MinHeap H = (MinHeap)malloc(sizeof(struct HNode));
 49     H->Data = (ElementType *)malloc((MaxSize+1)*sizeof(ElementType));
 50     H->Size = 0;
 51     H->Capacity = MaxSize;
 52     H->Data[0] = MINDATA; /* 定义"哨兵"为小于堆中所有可能元素的值*/
 53  
 54     return H;
 55 }
 56 
 57 bool IsFull( MinHeap H )
 58 {
 59     return (H->Size == H->Capacity);
 60 }
 61 
 62 /* 将元素X插入最小堆H，其中H->Data[0]已经定义为哨兵 */ 
 63 bool Insert( MinHeap H, ElementType X )
 64 {
 65     if ( IsFull(H) ) { 
 66         printf("最小堆已满");
 67         return false;
 68     }
 69     int i = ++H->Size; /* i指向插入后堆中的最后一个元素的位置 */
 70     for ( ; H->Data[i/2] > X; i /= 2 )
 71         H->Data[i] = H->Data[i/2]; /* 上滤X */
 72     H->Data[i] = X; /* 将X插入 */
 73     return true;
 74 }
 75 
 76 bool IsEmpty( MinHeap H )
 77 {
 78     return (H->Size == 0);
 79 }
 80 
 81 /* 从最小堆H中取出键值为最小的元素，并删除一个结点 */ 
 82 ElementType DeleteMin( MinHeap H )
 83 { 
 84     int Parent, Child;
 85     ElementType MinItem, X;
 86  
 87     if ( IsEmpty(H) ) {
 88         printf("最小堆已为空");
 89         return ERROR;
 90     }
 91  
 92     MinItem = H->Data[1]; /* 取出根结点存放的最小值 */
 93     /* 用最小堆中最后一个元素从根结点开始向上过滤下层结点 */
 94     X = H->Data[H->Size--]; /* 注意当前堆的规模要减小 */
 95     for( Parent = 1; Parent * 2 <= H->Size; Parent = Child ) {
 96         Child = Parent * 2;
 97         if( (Child != H->Size) && (H->Data[Child] > H->Data[Child+1]) )
 98             Child++;  /* Child指向左右子结点的较小者 */
 99         if( X <= H->Data[Child] ) break; /* 找到了合适位置 */
100         else  /* 下滤X */
101             H->Data[Parent] = H->Data[Child];
102     }
103     H->Data[Parent] = X;
104  
105     return MinItem;
106 } 
107 
108 /*----------- 建造最小堆 -----------*/
109 /* 下滤：将H中以H->Data[p]为根的子堆调整为最小堆 */
110 void PercDown( MinHeap H, int p )
111 {
112     int Parent, Child;
113     ElementType X;
114  
115     X = H->Data[p]; /* 取出根结点存放的值 */
116     for( Parent = p; Parent*2 <= H->Size; Parent = Child ) {
117         Child = Parent * 2;
118         if( (Child != H->Size) && (H->Data[Child] > H->Data[Child+1]) )
119             Child++;  /* Child指向左右子结点的较小者 */
120         if( X >= H->Data[Child] ) break; /* 找到了合适位置 */
121         else  /* 下滤X */
122             H->Data[Parent] = H->Data[Child];
123     }
124     H->Data[Parent] = X;
125 }
126 
127 /* 调整H->Data[]中的元素，使满足最大堆的有序性  */
128 /* 这里假设所有H->Size个元素已经存在H->Data[]中 */
129 void BuildHeap( MinHeap H )
130 {
131     /* 从最后一个结点的父节点开始，到根结点1 */
132     for(int i = H->Size/2; i > 0; i-- )
133         PercDown( H, i );
134 }

sj4_4

二.哈夫曼树与哈弗曼编码

1.哈夫曼树

带权路径长度(WPL)：设二叉树有n个叶子结点，每个叶子结点带有权值 Wk，从根结点到每个叶子结点的长度为 Lk，则每个叶子结点的带权路径长度之和就是：

　　　　　　WPL =

最优二叉树或哈夫曼树: WPL最小的二叉树

哈夫曼树的特点:
　　①没有度为1的结点

　　②n个叶子结点的哈夫曼树共有2n-1个结点

　　③哈夫曼树的任意非叶节点的左右子树交换后仍是哈夫曼树

　　④对同一组权值{w1 ,w2 , …… , wn}，存在不同构的两棵哈夫曼树

1.哈夫曼树的构造

每次把权值最小的两颗二叉树合并.(利用堆)

->-->--->---->

 1 //Huffman Tree
 2 typedef struct TreeNode *HuffmanTree;
 3 struct TreeNode{
 4     int weight;
 5     HuffmanTree left,right;
 6 }; 
 7 
 8 HuffmanTree Huffman(MinHeap H)
 9 {/*假设H->Size个权值已经存在在H->data[]->weight里*/
10     HuffmanTree T;
11     BuildMinHeap(H);//将H->data[]按权值调整为最小堆 
12     for(int i = 1; i < H->Size; i++) {//做H->Size-1次合并 
13         T = (HuffmanTree)malloc(sizeof(struct TreeNode));//建立新结点 
14         T->left = DeleteMin(H);    //从最小堆中删除一个结点，作为新T的左子结点 
15         T->right = DeleteMin(H);//从最小堆中删除一个结点，作为新T的右子结点
16         T->weight = T->left->weight + T->right->weight;//计算新权值
17         Insert(H,T);//将新T插入最小堆
18     }
19     T = DeleteMin(H);
20     return T;
21 }

View Code

2.哈弗曼编码

前缀码(prefix code)：任何字符的编码都不是另一字符编码的前缀
　　可以无二义地解码

构造一颗编码代价最小的二叉树:HaffumanTree

三.并查集

集合的表示
　　集合运算：交、并、补、差，判定一个元素是否属于某一集合
　　并查集：集合并、查某元素属于什么集合
　　并查集问题中集合存储如何实现：

①可以用树结构表示集合，树的每个结点代表一个集合元素

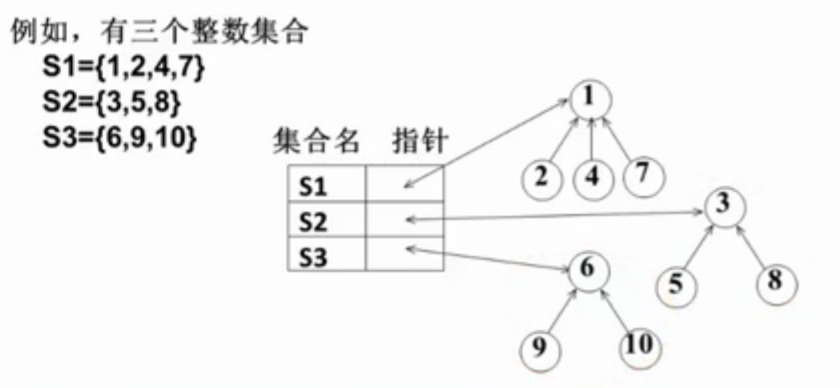
②采用数组存储形式

合并后根为负数，负数代表根，其绝对值代表个数。

1.查找某个元素所在的集合（用根结点表示）

1 SetName Find( ElementType S[], ElementType X )
2 { /* 默认集合元素全部初始化为-1 */
3     if ( S[X] < 0 ) /* 找到集合的根 */
4         return X;
5     else
6         return S[X] = Find( S, S[X] ); /* 路径压缩 */
7 }

View Code

2.集合的并运算

　　①分别找到X1和X2两个元素所在集合树的根结点
　　②如果它们不同根，则将其中一个根结点的父结点指针设置成另一个根结点的数组下标。

为了改善合并以后的查找性能，采用小的集合合并到相对大的集合中。

 1 /* 这里默认Root1和Root2是不同集合的根结点 */
 2 void Union( ElementType S[], SetName Root1, SetName Root2 )
 3 {
 4     /* 保证小集合并入大集合 */
 5     if ( S[Root2] < S[Root1] ) { /* 如果集合2比较大 */
 6         S[Root2] += S[Root1];     /* 集合1并入集合2  */
 7         S[Root1] = Root2;
 8     }
 9     else {                         /* 如果集合1比较大 */
10         S[Root1] += S[Root2];     /* 集合2并入集合1  */
11         S[Root2] = Root1;
12     }
13 }

View Code

相关阅读:
Android 密匙库导出
 Android常用布局
 asp.net hessian + android hessdroid
Android文件上传
 android,gridview
Android文件下载
 Andriod 之数据获取
 java类的泛型DAO
Spring之AOP编程
 mysql中如何统计某字段里某个字符的个数
原文地址：https://www.cnblogs.com/kuotian/p/5352249.html

数据结构学习笔记04树(堆 哈夫曼树 并查集)

数据结构学习笔记04树(堆哈夫曼树并查集)