G(x)
Time Limit: 2000/500 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 184 Accepted Submission(s): 44
Problem Description
For a binary number x with n digits (AnAn-1An-2 ... A2A1), we encode it as 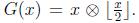
Where "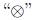 " is bitwise XOR operation and "
" is bitwise XOR operation and "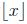 " indicates the largest integer which is not greater than x.
" indicates the largest integer which is not greater than x.
Due to some reasons, Mzry1992 encode his password P into G(P), and additionally, he encode P + 1 into G(P + 1) too, and write G(P) and G(P + 1) into his diary.
This story happened many years ago and now you hold the diary with these numbers in your hands. Unfortunately, some digits are unreadable now. Could you determine the values of these digits using the readable digits?
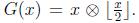
Where "
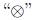 " is bitwise XOR operation and "
" is bitwise XOR operation and "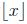 " indicates the largest integer which is not greater than x.
" indicates the largest integer which is not greater than x.Due to some reasons, Mzry1992 encode his password P into G(P), and additionally, he encode P + 1 into G(P + 1) too, and write G(P) and G(P + 1) into his diary.
This story happened many years ago and now you hold the diary with these numbers in your hands. Unfortunately, some digits are unreadable now. Could you determine the values of these digits using the readable digits?
Input
The first line has a number T (T <= 100) , indicating the number of test cases.
For every test case, it has 2 lines of same number of digits describe G(P) and G(P + 1), In every line, it only contains 1, 0 and ?. Unreadable digits are denoted with symbol ?, The length of every line in the input is up to 105.
For every test case, it has 2 lines of same number of digits describe G(P) and G(P + 1), In every line, it only contains 1, 0 and ?. Unreadable digits are denoted with symbol ?, The length of every line in the input is up to 105.
Output
For every case, you should output "Case #t: " at first, without quotes. The t is the case number starting from 1.
Then, if there is impossible to restore G(P) and G(P + 1), you should output "Impossible" in the second line.
Otherwise, if G(P) is unique, you should output restored G(P) and G(P +1) in the same format.
Otherwise, you should output "Ambiguous" and the number of possible G(P) in the second line.
The number may be very large so the answer should modulo 10^9 + 7.
Then, if there is impossible to restore G(P) and G(P + 1), you should output "Impossible" in the second line.
Otherwise, if G(P) is unique, you should output restored G(P) and G(P +1) in the same format.
Otherwise, you should output "Ambiguous" and the number of possible G(P) in the second line.
The number may be very large so the answer should modulo 10^9 + 7.
Sample Input
3
10??
10??
0010
0110
1?01
0?01
Sample Output
Case #1:
Ambiguous 3
Case #2:
0010
0110
Case #3:
Impossible
Hint
In the first sample case, the three possible situations are:
1.
G(12) = 1010
G(13) = 1011
2.
G(13) = 1011
G(14) = 1001
3.
G(14) = 1001
G(15) = 1000
Source
Recommend
liuyiding
很容易找出规律,
然后递推,枚举就解决了。
P和P+1 其实就是差后面一点
P: XXXXX 0 1 1 1
P+1: XXX 1 0 0 0
关键点就是枚举P的第一个0的位置。左边的P和P+1是一样的。
1 /* *********************************************** 2 Author :kuangbin 3 Created Time :2013/9/14 星期六 14:16:53 4 File Name :2013成都网络赛1006.cpp 5 ************************************************ */ 6 7 #pragma comment(linker, "/STACK:1024000000,1024000000") 8 #include <stdio.h> 9 #include <string.h> 10 #include <iostream> 11 #include <algorithm> 12 #include <vector> 13 #include <queue> 14 #include <set> 15 #include <map> 16 #include <string> 17 #include <math.h> 18 #include <stdlib.h> 19 #include <time.h> 20 using namespace std; 21 22 const int MAXN = 100010; 23 const int MOD = 1e9+7; 24 char str1[MAXN], str2[MAXN]; 25 int dp[MAXN][2]; 26 int flag[MAXN][2]; 27 28 char sss1[MAXN],sss2[MAXN]; 29 30 int main() 31 { 32 //freopen("in.txt","r",stdin); 33 //freopen("out.txt","w",stdout); 34 int T; 35 int iCase = 0; 36 scanf("%d",&T); 37 while(T--) 38 { 39 iCase++; 40 printf("Case #%d: ",iCase); 41 scanf("%s%s",str1,str2); 42 int n = strlen(str1); 43 dp[0][0] = 1; 44 dp[0][1] = 0; 45 flag[0][0] = 1; 46 flag[0][1] = 0; 47 for(int i = 1;i <= n;i++) 48 { 49 if(str1[i-1] == '?' && str2[i-1] == '?') 50 { 51 dp[i][1] = dp[i-1][0] + dp[i-1][1]; 52 dp[i][0] = dp[i-1][0] + dp[i-1][1]; 53 int tmp = flag[i-1][0] + flag[i-1][1]; 54 if(tmp == 0) 55 flag[i][0] = flag[i][1] = 0; 56 else if(tmp == 1) 57 flag[i][0] = flag[i][1] = 1; 58 else flag[i][0] = flag[i][1] = 2; 59 } 60 else if(str1[i-1] == '?' || str2[i-1] == '?') 61 { 62 if(str1[i-1] == '0' || str2[i-1] =='0') 63 { 64 dp[i][1] = dp[i-1][1]; 65 dp[i][0] = dp[i-1][0]; 66 flag[i][0] = flag[i-1][0]; 67 flag[i][1] = flag[i-1][1]; 68 } 69 else if(str1[i-1] == '1' || str2[i-1] =='1') 70 { 71 dp[i][1] = dp[i-1][0]; 72 dp[i][0] = dp[i-1][1]; 73 flag[i][1] = flag[i-1][0]; 74 flag[i][0] = flag[i-1][1]; 75 } 76 } 77 else if(str1[i-1] != str2[i-1]) 78 { 79 dp[i][0] = dp[i][1] = 0; 80 flag[i][0] = flag[i][1] = 0; 81 } 82 else 83 { 84 if(str1[i-1] =='0') 85 { 86 dp[i][0] = dp[i-1][0]; 87 dp[i][1] = dp[i-1][1]; 88 flag[i][0] = flag[i-1][0]; 89 flag[i][1] = flag[i-1][1]; 90 91 } 92 else 93 { 94 dp[i][0] = dp[i-1][1]; 95 dp[i][1] = dp[i-1][0]; 96 flag[i][1] = flag[i-1][0]; 97 flag[i][0] = flag[i-1][1]; 98 } 99 } 100 if(dp[i][0] >= MOD)dp[i][0] -= MOD; 101 if(dp[i][1] >= MOD)dp[i][1] -= MOD; 102 } 103 int ans = 0; 104 int flag_num = 0; 105 int ss_id = -1; 106 for(int i = n;i > 0;i--) 107 { 108 if(i+2 <= n) 109 { 110 if(str1[i+1] == '1' || str2[i+1] == '1') 111 break; 112 } 113 if(i+1 <= n) 114 { 115 if(str1[i] == '0' || str2[i] == '0') 116 continue; 117 } 118 if(i-1 >= 0) 119 { 120 if(str1[i-1] == str2[i-1] && str1[i-1] != '?') 121 continue; 122 } 123 char ch; 124 if(str1[i-1] == str2[i-1] && str1[i-1] == '?') 125 { 126 ans += dp[i-1][0]; 127 ans %= MOD; 128 ans += dp[i-1][1]; 129 ans %= MOD; 130 flag_num += flag[i-1][0] + flag[i-1][1]; 131 if(flag_num > 2)flag_num = 2; 132 } 133 else 134 { 135 if(str1[i-1] != '?')ch = str1[i-1]; 136 else 137 { 138 if(str2[i-1] == '0')ch = '1'; 139 else ch = '0'; 140 } 141 if(ch == '0') 142 { 143 ans += dp[i-1][0]; 144 ans %= MOD; 145 flag_num += flag[i-1][0]; 146 if(flag_num > 2)flag_num = 2; 147 } 148 else 149 { 150 ans += dp[i-1][1]; 151 ans %= MOD; 152 flag_num += flag[i-1][1]; 153 if(flag_num > 2)flag_num = 2; 154 } 155 } 156 if(flag_num == 1 && ss_id == -1)ss_id = i; 157 } 158 if(flag_num == 0) 159 { 160 printf("Impossible "); 161 continue; 162 } 163 if(flag_num > 1) 164 { 165 printf("Ambiguous %d ",ans); 166 continue; 167 } 168 if(flag_num == 1) 169 { 170 sss1[n] = sss2[n] = 0; 171 sss1[ss_id-1] = '0'; 172 sss2[ss_id-1] = '1'; 173 for(int i = ss_id;i < n;i++) 174 sss1[i] = '1', sss2[i] = '0'; 175 int last = 0; 176 for(int i = ss_id-2;i >= 0;i--) 177 { 178 int now; 179 if(flag[i+1][0] > 0)now = 0; 180 else now = 1; 181 sss1[i] = sss2[i] = '0' + now; 182 183 } 184 for(int i = n-1; i > 0;i--) 185 { 186 if(sss1[i-1] ==sss1[i])sss1[i] = '0'; 187 else sss1[i] = '1'; 188 if(sss2[i-1] == sss2[i])sss2[i] = '0'; 189 else sss2[i] = '1'; 190 } 191 192 printf("%s %s ",sss1,sss2); 193 continue; 194 } 195 cout<<ans<<endl; 196 197 198 } 199 return 0; 200 }