我们可以为二叉树 T 定义一个翻转操作,如下所示:选择任意节点,然后交换它的左子树和右子树。
只要经过一定次数的翻转操作后,能使 X 等于 Y,我们就称二叉树 X 翻转等价于二叉树 Y。
编写一个判断两个二叉树是否是翻转等价的函数。这些树由根节点 root1 和 root2 给出。
示例:
输入:root1 = [1,2,3,4,5,6,null,null,null,7,8], root2 = [1,3,2,null,6,4,5,null,null,null,null,8,7] 输出:true 解释:我们翻转值为 1,3 以及 5 的三个节点。
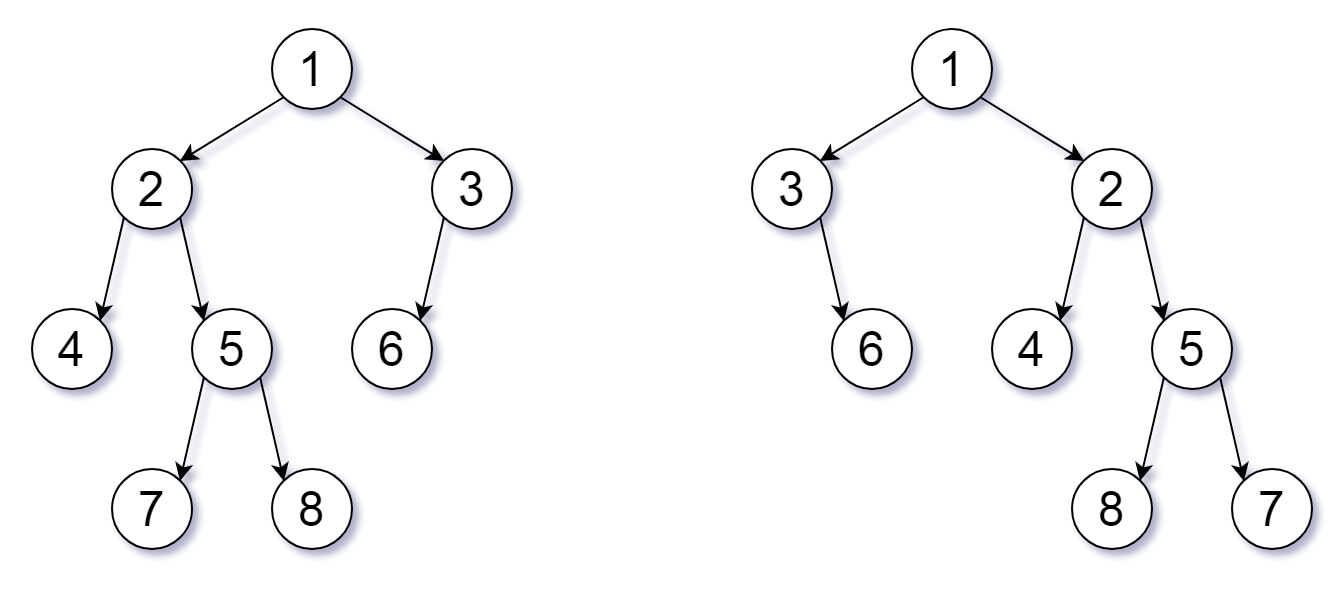
方法一: 递归 思路 如果二叉树 root1,root2 根节点值相等,那么只需要检查他们的孩子是不是相等就可以了。 算法 存在三种情况: 如果 root1 或者 root2 是 null,那么只有在他们都为 null 的情况下这两个二叉树才等价。 如果 root1,root2 的值不相等,那这两个二叉树的一定不等价。 如果以上条件都不满足,也就是当 root1 和 root2 的值相等的情况下,需要继续判断 root1 的孩子节点是不是跟 root2 的孩子节点相当。因为可以做翻转操作,所以这里有两种情况需要去判断。
class Solution { public boolean flipEquiv(TreeNode root1, TreeNode root2) { if (root1 == root2) return true; if (root1 == null || root2 == null || root1.val != root2.val) return false; return (flipEquiv(root1.left, root2.left) && flipEquiv(root1.right, root2.right) || flipEquiv(root1.left, root2.right) && flipEquiv(root1.right, root2.left)); } }