【poj 2976】Dropping tests（算法效率--01分数规划 模版题+二分）｛附【转】01分数规划问题｝

P.S.又是一个抽时间学了2个小时的新东西......讲解在上半部分，题解在下半部分。

先说一下转的原文：http://www.cnblogs.com/perseawe/archive/2012/05/03/01fsgh.html
我挑选部分转了过来：01分数规划问题

定义：给定两个数组，a[i]表示选取i的收益，b[i]表示选取i的代价。如果选取i，定义x[i]=1否则x[i]=0。每一个物品只有选或者不选两种方案，求一个选择方案使得R=sigma(a[i]*x[i])/sigma(b[i]*x[i])取得最值，即所有选择物品的总收益/总代价的值最大或是最小。
      01分数规划问题主要包含一般的01分数规划、最优比率生成树问题、最优比率环问题、最大密度子图等。

具体分析：数学分析中一个很重要的方法就是分析目标式，这样我们来看目标式。R=sigma(a[i]*x[i])/sigma(b[i]*x[i])。
      我们先定义一个函数F(L):=sigma(a[i]*x[i])-L*sigma(b[i]*x[i])，显然这只是对目标式的一个简单的变形。分离参数，得到F(L):=sigma((a[i]-L*b[i])*x[i])。
      这时我们就会发现，如果L已知的话，a[i]-L*b[i]就是已知的，当然x[i]是未知的。记d[i]=a[i]-L*b[i]，那么F(L):=sigma(d[i]*x[i])，多么简洁的式子。我们就对这些东西下手了。

我们来分析一下这个函数，它与目标式的关系非常的密切，L就是目标式中的R，最大化R也就是最大化L。

F的值是由两个变量共同决定的，即方案X和参数L。对于一个确定的参数L来说，方案的不同会导致对应的F值的不同，那么这些东西对我们有什么用呢?
     假设我们已知在存在一个方案X使得F(L)>0，这能够证明什么?
     F(L)=sigma(a[i]*x[i])-L*sigma(b[i]*x[i])>0即sigma(a[i]*x[i])/sigma(b[i]*x[i])>L也就是说，如果一个方案使得F(L)>0说明了这组方案可以得到一个比现在的L更优的一个L，既然有一个更优的解，那么为什么不用呢？
     显然，d数组是随着L的增大而单调减的。也就是说，存在一个临界的L使得不存在一种方案，能够使F(L)>0. 我们猜想，这个时候的L就是我们要求的最优解。之后更大的L值则会造成无论任何一种方案，都会使F(L)<0.类似于上面的那个变形，我们知道，F(L)<0是没有意义的，因为这时候的L是不能够被取得的。当F(L)=0使，对应方案的R值恰好等于此时的L值。

     综上，函数F(L)有这样的一个性质：在前一段L中可以找到一组对应的X使得F(L)>0，这就提供了一种证据，即有一个比现在的L更优的解，而在某个L值使，存在一组解使得F(L)=0,且其他的F(L)<0，这时的L无法继续增大，即这个L就是我们期望的最优解，之后的L会使得无论哪种方案都会造成F(L)<0.而我们已经知道，F(L)<0是没有任何意义的，因为此时的L值根本取不到。

     如果现在你觉得有些晕的话，那么我要提醒你的就是，我们的目标是R！！！千万不要把F值同R值混淆。F值是根据我们的变形式求的D数组来计算的，而R值则是我们所需要的真实值，他的计算是有目标式决定的。F值只是提供了一个证据，告诉我们真正最优的R值在哪里，他与R值本身并没有什么必然的联系。

解法：二分和Dinkelbach算法。
  1.根据这样的一段性质，很自然的就可以想到二分L值，然后验证是否存在一组解使得F(L)>0，有就移动下界，没有就移动上界。
     所有的01分数规划都可以这么做，唯一的区别就在于求解时的不同——因为每一道题的限制条件不同，并不是每一个解都是可行解的。比如在普通的数组中，你可以选取1、2、3号元素，但在生成树问题中，假设1、2、3号元素恰好构成了一个环，那就不能够同时选择了，这就是需要具体问题，具体分析的部分。
     二分是一个非常通用的办法，但是我们来考虑这样的一个问题，二分的时候我们只是用到了F(L)>0这个条件，而对于使得F(L)>0的这组解所求到的R值没有使用。因为F(L)>0,我们已经知道了R是一个更优的解，与其漫无目的的二分，为什么不将解移动到R上去呢？)
   2.求01分数规划的另一个方法就是Dinkelbach算法，他就是基于这样的一个思想，他并不会去二分答案，而是先随便给定一个答案，然后根据更优的解不断移动答案，逼近最优解。由于他对每次判定使用的更加充分，所以它比二分会快上很多。但是，他的弊端就是需要保存这个解，而我们知道，有时候验证一个解和求得一个解的复杂度是不同的。

二分和Dinkelbach算法写法都非常简单，各有长处，大家要根据题目谨慎使用。
 

---

poj 2976 Dropping tests

题意：有 N 对 (ai,bi) ，要求选 N-K 对，使得 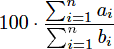。请输出该式子的最大值，输出整数。

解法：如上面所说的 01分数规划。下面附上2个代码。二分的157ms

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<iostream>
using namespace std;

const int N=1010,D=(int)1e9+10;
const double eps=1e-6;
int n,k;
double a[N],b[N],d[N];

bool cmp(int x,int y) {return x>y;}
int main()
{
    while (1)
    {
      scanf("%d%d",&n,&k);
      if (!n && !k) break;
      for (int i=1;i<=n;i++) scanf("%lf",&a[i]);
      for (int i=1;i<=n;i++) scanf("%lf",&b[i]);
      double l,r,mid=0.0000000,h;
      for (int i=1;i<=n;i++)
        if (a[i]/b[i]>mid) mid=a[i]/b[i];
      l=0.0000000,r=mid;
      while (r-l>eps)
      {
        mid=(l+r)/2, h=0;
        for (int i=1;i<=n;i++)
          d[i]=a[i]-b[i]*mid;
        sort(d+1,d+1+n,cmp);
        for (int i=1;i<=n-k;i++)
          h+=d[i];
        //printf("%.6lf %.6lf %.6lf %.6lf
",l,mid,r,h);
        if (h>=0.0000000) l=mid;
        else r=mid-eps;
      }
      printf("%d
",(int)(r*100.0000000+0.5000000));
    }
    return 0;
}

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<iostream>
using namespace std;

const int N=1010,D=(int)1e9+10;
const double eps=1e-6;
int n,k;
struct node{double a,b,d;}s[N];

bool cmp(node x,node y) {return x.d>=y.d;}
int main()
{
    while (1)
    {
      scanf("%d%d",&n,&k);
      if (!n && !k) break;
      for (int i=1;i<=n;i++) scanf("%lf",&s[i].a);
      for (int i=1;i<=n;i++) scanf("%lf",&s[i].b);
      double t,ans,p,q;
      ans=1.0000000;
      while (1)
      {
        t=ans;//t为设的值
        for (int i=1;i<=n;i++)
          s[i].d=s[i].a-s[i].b*t;
        sort(s+1,s+1+n,cmp);
        p=q=0.0000000;
        for (int i=1;i<=n-k;i++)
          p+=s[i].a,q+=s[i].b;
        ans=p/q;//实际值
        if (ans-t<eps) break;
      }
      printf("%d
",(int)(ans*100.0000000+0.5000000));
    }
    return 0;
}