线段与圆是否相交

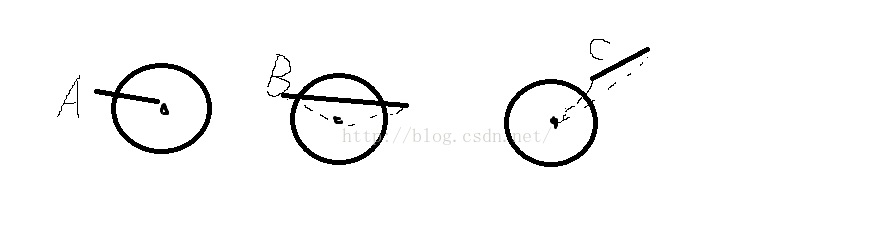
1. 如图A所示，当圆心与线段的距离大于圆的半径时，线段与圆肯定不相交

2. 如图B,C所示，两个端点都不在圆内，那么看圆心到线段所在直线的垂足是否小于半径且垂足是否在线段上；我们可以利用余弦定理，避免判断垂足是否在线段上，只要圆心到两端点的得角度都为锐角，那么他们必然相交。

https://www.cnblogs.com/bryce1010/p/9387351.html

---

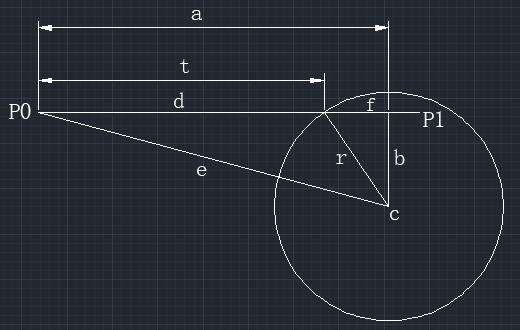
如上图用圆心c和半径r来定义圆，线段的定义为：p(t)=p0+td，这里d为单位向量，t从0变化到l，l为线段长度。所要求的是交点处t的值：
(t = a - f)
a的计算方法如下，设e为从p0直线圆心c的向量：
(e = c - p0)
(a = e.d（点乘）  （此式看不明白的请参考向量投影相关知识）)
现在的任务就是计算f。首先，根据勾股定理，可以很清楚地得到：
(f^2+b^2=r^2)
在较大的三角形中用勾股定理求得(b^2):
(a^2 + b^2=e^2)
(b^2 = e^2-a^2)
e是从线段起点到圆心之间的距离，也就是向量e的长度，因此，(e^2):
  (e^2 = e.e)
代入并化简得：
(f = sqrt(r^2-e^2+a^2))
最后求得t:
 (t = a - f)
这里考虑开根号出来的正负两种情况，从而得到两个交点。
这里注意为负，那么射线与圆不相交。

如上图，如果存在交点，则另一个交点只需要计算：(t+2f)

Unity C#:

using System.Collections;
using UnityEngine;

public static class GeomUtil {

    /// <summary>
    /// 计算线段与圆的交点
    /// </summary>
    /// <param name="lineStart"> 线段的起始点 </param>
    /// <param name="lineEnd"> 线段的终点 </param>
    /// <param name="circleCenter"> 圆心 </param>
    /// <param name="radius"> 半径 </param>
    /// <param name="intersection1"> 输出的交点1 </param>
    /// <param name="intersection2"> 输出的交点2 </param>
    /// <returns> 返回交点的数量，0：不相交；1：有1个交点；2：有2个交点 </returns>
    public static int LineSegmentIntersectCircle (Vector2 lineStart, Vector2 lineEnd, Vector2 circleCenter, float radius, out Vector2 intersection1, out Vector2 intersection2) {
        int intersectCount = 0;
        bool intersect = Ray2DIntersectCircle(lineStart, lineEnd - lineStart, circleCenter, radius, out intersection1, out intersection2);
        if (intersect) {
            float lineSegmentLength = Vector2.Distance(lineStart, lineEnd);
            float d1 = Vector2.Distance(lineStart, intersection1 - lineStart);
            float d2 = Vector2.Distance(lineStart, intersection2 - lineStart);
            if (d1 <= lineSegmentLength) {
                intersectCount++;
            }
            if (d2 <= lineSegmentLength) {
                intersectCount++;
            }
        }
        return intersectCount;
    }

    /// <summary>
    /// 计算射线与圆的交点
    /// </summary>
    /// <param name="ray"> 2D射线 </param>
    /// <param name="circleCenter"> 圆心 </param>
    /// <param name="radius"> 半径 </param>
    /// <param name="intersection1"> 输出的交点1 </param>
    /// <param name="intersection2"> 输出的交点2 </param>
    /// <returns> 是否相交 </returns>
    public static bool Ray2DIntersectCircle (Ray2D ray, Vector2 circleCenter, float radius, out Vector2 intersection1, out Vector2 intersection2) {
        intersection1 = Vector2.zero;
        intersection2 = Vector2.zero;

        Vector2 e = circleCenter - ray.origin;
        float a = Vector2.Dot(ray.direction, e);
        float fSqr = radius * radius - e.sqrMagnitude + a * a;
        if (fSqr >= 0) {
            float f = Mathf.Sqrt(fSqr);
            float t = a - f;
            if (t >= 0) {
                intersection1 = ray.origin + ray.direction * t;
                intersection2 = ray.origin + ray.direction * (t + 2f * f);
                return true;
            }
        }
        return false;
    }

    /// <summary>
    /// 计算射线与圆的交点
    /// </summary>
    /// <param name="origin"> 2D射线的原点 </param>
    /// <param name="direction"> 2D射线的方向 </param>
    /// <param name="circleCenter"> 圆心 </param>
    /// <param name="radius"> 半径 </param>
    /// <param name="intersection1"> 输出的交点1 </param>
    /// <param name="intersection2"> 输出的交点2 </param>
    /// <returns> 是否相交 </returns>
    public static bool Ray2DIntersectCircle (Vector2 origin, Vector2 direction, Vector2 circleCenter, float radius, out Vector2 intersection1, out Vector2 intersection2) {
        Ray2D ray = new Ray2D(origin, direction);
        return Ray2DIntersectCircle(ray, circleCenter, radius, out intersection1, out intersection2);
    }
}