一般都说测试先做单元测试,然后做集成测试,然后做系统测试之类的,其实说白了,也可以理解成将最基本的测试步骤,或者说测试环境使用一定的方法组合以后再生成新的测试用例。因为人工组合,第一比较费神,第二是有时要么是设计了几个等价的测试用例,重复执行这些等价的测试用例,比较费时。这里有一个比较好的测试技术,叫做配对(pair-wise)测试,它可以根据你设定的条件,自动生成在测试时间(即工作量)和测试覆盖率之间做出平衡的组合。
配对测试的基本理念是,虽然程序的某个组件,或者程序自己会接受很多的输入,但大部分情况下,程序的bug不是因为这些输入同时作用而产生的,而是由一到两个输入条件同时作用导致的。因此配对测试在生成测试组合的时候,主要关注将每个条件与其它条件至少配对一次,而不是试图生成全组合,这样就可以大大减少需要测试的组合数,尽而节省测试工作量,同时又能达到满意的测试覆盖率。
当然不能期望配对测试是万能的,即我们仅依赖于配对测试自动生成的测试用例就可以了,使用配对测试的目的是为了减少测试人员浪费在执行太多的等价组合的时间,将宝贵的时间尽可能地放在设计符合用户使用场景的测试用例上。
具体示例(手工步骤)
废话少说,先看一个具体的示例,假设我们有下面一个产品,界面如下:
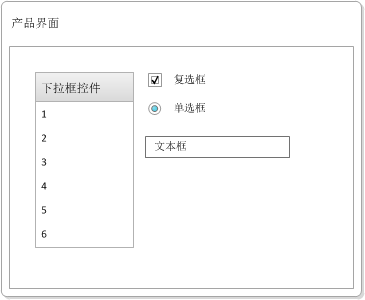
对于上面这个产品(假设文本框接受1到100之间的整数),可以将测试条件划分为下面这样子:

当然,文本框的条件我们还可以再细分一下,但是为了描述简单,我把条件设置的比较粗糙,如果按照全组合的用例设置方式,需要 6 (下拉框控件可能的条件) * 2 (复选框可能的条件) * 2 (单选框可能的条件) * 6 (文本框可能的条件) = 144个组合。
我们来看使用配对方式设计组合的方式:
1. 先将上面的条件输入到Excel里,并在列头标明可能出现的条件的个数,并按条件的个数将各个输入参数排序,如下图所示:
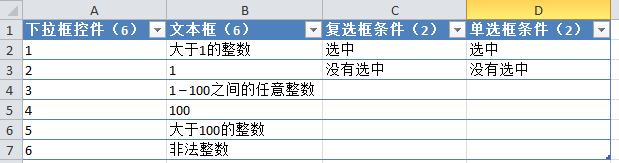
2. 先将第二个和第三个参数的各个条件组合一次,这里为了省事起见,我先去掉第一个参数,只介绍第二、三、四个参数的配对组合方法:
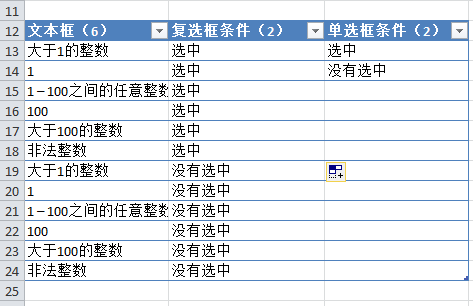
3. 然后再将第二个参数和第四个参数的各个条件组合一次,如下图所示:
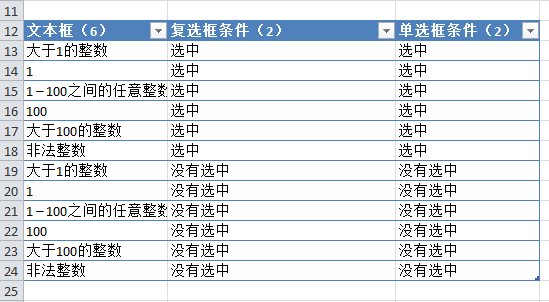
4. 为了确保第四个参数跟第三个参数的各个条件都有一次组合,可以使用Excel提供的过滤功能来判断,例如下图中,很明显,两个参数没有一个完全组合:
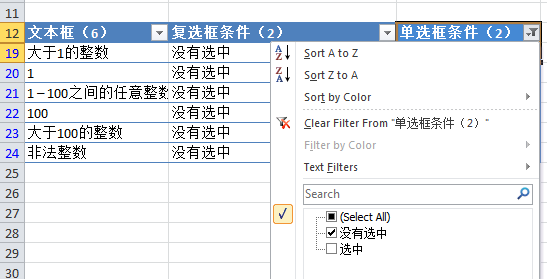
5. 解决方案很简单,只需要再添加两行,将两个参数中没有组合的条件各自组合一次好了(当然,你也可以将第四个参数的条件稍微调整一下达到相同的目的):

自动化步骤
上面的工作还是有点繁琐,实际上早已有人将这个过程自动化了,这里介绍一个免费开源的工具allpairs.exe,请于下面这个链接里下载:
http://www.satisfice.com/tools/pairs.zip
对于上面的例子,使用allpairs生成组合的方式是:
1. 先将上面的条件输入到Excel里,如下图所示(因为这个工具是老外写得,没有考虑支持中文的问题,所以最好全部用英文表示):

2. 将Excel文件保存为以Tab键作为分隔符的文本文件:

3. 然后使用allpairs.exe处理这个文件:
allpairs.exe test.txt > output.txt
4. 在output.txt里,PAIRING DETAILS下面的东西都是没有用的,可以直接删掉,删掉以后,结果如下:
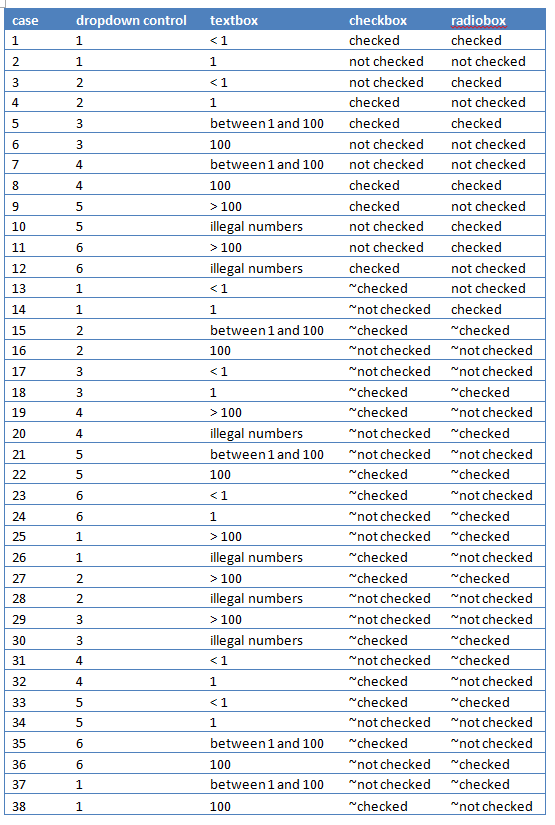
你可以在设计测试环境矩阵还有组合测试用例的时候使用allpairs这个技术,当然,你不能完全依赖这个技术,除了allpairs组合的测试用例以外,你最好再根据测试覆盖率和用户场景覆盖率入手,补充更有价值的测试用例。
另外,使用配对测试的算法,我们有可能结合Behavior Driven Design技术,直接从需求自动生成测试用例,加之如果我们将基本的测试用例自动化以后,完全可以使用这个技术将自动化过的测试用例配对组合(当然需要加上一些限制条件),在节省测试时间的同时,达到满意的测试覆盖率,当然,这样做要求我们自己写一个测试工具来实现这个技术—至少到现在我还没有看到现成的工具,而且这个技术应该要比模型驱动测试更容易使用,因为模型驱动测试的问题是建模太困难。