官网:http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html
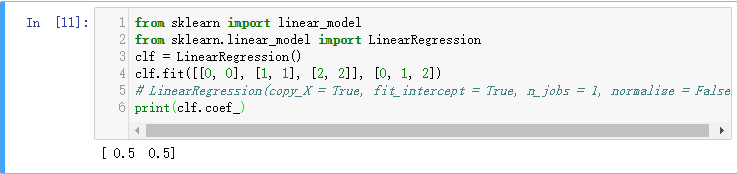
class sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=1)
线性回归参数:
fit_intercept:布尔值,默认为true
说明:是否对训练数据进行中心化。为false,表明输入的数据已经进行了中心化,在下面过程不进行中心化处理;否则,对输入的数据进行中心化处理。(intercept 拦截)
normalize:布尔型,默认为false
说明:是否对数据进行标准化处理。(normalize 使标准化)
copy_X:布尔型,默认为true
说明:是否对X复制,为false,直接对原数据进行覆盖。即经过中心化,标准化后,是否把新数据覆盖到原数据上。
n_jobs:整型,默认为1
说明:计算时设置的任务个数(number of jobs)。为-1,代表所有的CPU。这一参数对于目标个数>1(n_targets > 1)且足够大规模的问题有加速作用。
返回值:
coef_:数组型变量,形状为(n_features,)或(n_targets, n_features)
说明:计算得到feature的系数。如果输入的是多目标问题,则返回一个二维数组(n_targets, n_features);如果是单目标问题,返回一个一维数组(n_features)。
intercept_:数组型变量
说明:线性模型中的独立项
注意:
1. 该算法仅仅是scipy.linalg.lstsq经过封装后的估计器。
2. 返回值coef_,intercept_在fit(X, y[, n_jobs])方法学习完后值会更准确。
方法:
decision_function(X):对训练数据X进行预测
fit(X, y[, n_jobs]):对训练集X, y进行训练。是对scipy.linalg.lstsq的封装
get_params([deep]):得到该估计器(estimator)的参数
predict(X):使用训练得到的估计器对输入为X的集合进行预测(X可以是测试集,也可以是需要预测的数据)
score(X, y, sample_weight=None):返回对于以X为samples,以y为target的预测效果评分。
set_params(**params):设置估计器的参数
decision_function(X)和predict(X)都是利用预估器对训练数据X进行预测,其中decision_function(X)包含了对输入数据的类型检查,以及当前对象是否存在coef_属性的检查,是一种“安全的”方法,而predict是对decision_function的调用。
score(X, y, sample_weight=None) 定义为(1-u/v),其中u = ((y_true - y_pred) ** 2).sum(),而v = ((y_true - y_true.mean())**2).mean()
最好的得分1.0,一般都比1.0低,得分越低代表结果越差。其中sample_weight为(samples_n,)形状的向量,可以指定对于某些sample的权值,如果觉得某些数据比较重要,可以将其的权值设置的大一些。