Leetcode 222.完全二叉树的节点个数

完全二叉树的节点个数

给出一个完全二叉树，求出该树的节点个数。

说明：

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^h 个节点。

示例:

输入:

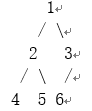
输出: 6

public class Solution {

    // 获取左子树的高度(其实是最左侧分支）
    public int getLeftHeight(TreeNode root) {
        int count = 0;
        while (root != null) {
            count++;
            root = root.left;
        }
        return count;
    }

    // 获取右子树的高度（其实是最右侧分支的高度）
    public int getRightHeight(TreeNode root) {
        int count = 0;
        while (root != null) {
            count++;
            root = root.right;
        }
        return count;
    }

    public int countNodes(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftHeight = getLeftHeight(root);
        int rightHeight = getRightHeight(root);

        if (leftHeight == rightHeight) {
            // 表示是满二叉树，二叉树的节点数直接由公式2^n-1得到
            // leftHeight即为层数， 1 << leftHeight使用位运算计算2^leftHeight，效率更高
            // 注意(1 << leftHeight) - 1 的括号必须有！！
            return (1 << leftHeight) - 1;
        } else {
            // 若该二叉树不是满二叉树，递归的调用该方法，计算左子树和右子树的节点数
            return countNodes(root.left) + countNodes(root.right) + 1;
        }
    }
}