题目
给定单链表头指针和一个结点指针,定义一个函数在O(1)时间内删除该结点。
分析
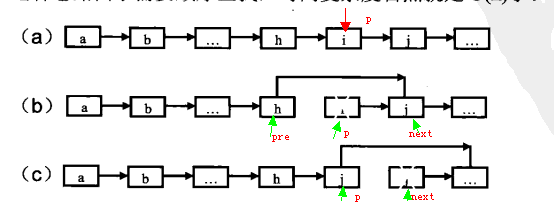
对于上图实例链表(a)删除指针p有两种方式
- 思路1:(b)找到前一个指针pre,赋值pre->next = p->next,删掉p
- 思路2:(c)目的是删除p,但是不删p,直接用p->next的值赋值给p,把p->next删除掉(好处:不用遍历找到p的前一个指针pre,O(1)时间内搞定)
于是,定位到思路2,但是思路2有两个特例:
- 删除的是尾指针,需要遍历找到前一个指针
- 整个链表就一个结点(属于删尾指针,但没法找到前面的指针,需要开小灶单独处理)
大体算法思路
待删指针不是尾指针:
待删指针的值用待删指针的下一个指针的值覆盖
删掉待删指针的下一个指针
待删指针是尾指针:
待删指针同时是头指针:
删掉头指针
待删指针不是头指针
找到待删指针的前一个指针
删掉待删指针,前一个指针的next赋值为空
参考代码
bool deleteNode(ListNode *&head, ListNode *p) { if(!p || !head) return false; if(p->m_pNext != NULL) //不是尾指针 { ListNode *del = p->m_pNext; p->m_nValue = del->m_nValue; p->m_pNext = del->m_pNext; delete del; del = NULL; } else if(head == p) //是尾指针,同时只有一个结点 { delete p; head = NULL; } else //是尾指针,同时有多个结点 { ListNode *tmp = NULL, *pre = head; while(pre->m_pNext != p) { pre = pre->m_pNext; } delete p; p = NULL; pre->m_pNext = NULL; } return true; }
完整代码1

#include <iostream> using namespace std; struct ListNode { int m_nValue; ListNode* m_pNext; }; bool deleteNode(ListNode *&head, ListNode *p) { if(!p || !head) return false; if(p->m_pNext != NULL) { ListNode *del = p->m_pNext; p->m_nValue = del->m_nValue; p->m_pNext = del->m_pNext; delete del; del = NULL; } else if(head == p) { delete p; head = NULL; } else { ListNode *tmp = NULL, *pre = head; while(pre->m_pNext != p) { pre = pre->m_pNext; } delete p; p = NULL; pre->m_pNext = NULL; } return true; } void createList(ListNode *&head) { head = new(ListNode); head->m_nValue = 1; head->m_pNext = NULL; ListNode *p2 = new(ListNode); p2->m_nValue = 2; p2->m_pNext = NULL; head->m_pNext = p2; ListNode *p3 = new(ListNode); p3->m_nValue = 3; p3->m_pNext = NULL; p2->m_pNext = p3; ListNode *p4 = new(ListNode); p4->m_nValue = 4; p4->m_pNext = NULL; p3->m_pNext = p4; } void deleteList(ListNode *p) { ListNode *next = NULL; while(p != NULL) { cout << p->m_nValue << endl; next = p->m_pNext; delete p; p = NULL; p = next; } } int main() { ListNode *head = NULL; createList(head); ListNode *p = head->m_pNext->m_pNext->m_pNext; deleteNode(head, p); deleteList(head); }
完整代码2

#include <iostream> using namespace std; struct ListNode { int m_nValue; ListNode* m_pNext; }; bool deleteNode(ListNode **head, ListNode *p) { if(!p || !head) return false; if(p->m_pNext != NULL) { ListNode *del = p->m_pNext; p->m_nValue = del->m_nValue; p->m_pNext = del->m_pNext; delete del; del = NULL; } else if(*head == p) { delete p; *head = NULL; } else { ListNode *tmp = NULL, *pre = *head; while(pre->m_pNext != p) { pre = pre->m_pNext; } delete p; p = NULL; pre->m_pNext = NULL; } return true; } void createList(ListNode *&head) { head = new(ListNode); head->m_nValue = 1; head->m_pNext = NULL; ListNode *p2 = new(ListNode); p2->m_nValue = 2; p2->m_pNext = NULL; head->m_pNext = p2; ListNode *p3 = new(ListNode); p3->m_nValue = 3; p3->m_pNext = NULL; p2->m_pNext = p3; ListNode *p4 = new(ListNode); p4->m_nValue = 4; p4->m_pNext = NULL; p3->m_pNext = p4; } void deleteList(ListNode *p) { ListNode *next = NULL; while(p != NULL) { cout << p->m_nValue << endl; next = p->m_pNext; delete p; p = NULL; p = next; } } int main() { ListNode *head = NULL; createList(head); ListNode *p = head->m_pNext->m_pNext; deleteNode(&head, p); deleteList(head); }
分析
删除非尾结点时间复杂读为O(1),删除尾结点的时间复杂读为O(n), 平均时间复杂度为[(n-1)*O(1) + O(N)] / N = O(1)
还有删除函数并不能处理待删结点就是该链表中的指针,因此需要人为调用时控制,如果得验证的话,那就没必要做这些处理了,直接O(N)
技术细节——传值操作
#include <iostream> using namespace std; struct ListNode { int m_nValue; ListNode* m_pNext; }; void createList(ListNode *head) { head = new(ListNode); head->m_nValue = 1; head->m_pNext = NULL; } void deleteList(ListNode *p) { ListNode *next = NULL; while(p != NULL) { cout << p->m_nValue << endl; next = p->m_pNext; delete p; p = NULL; p = next; } } int main() { ListNode *head = NULL; createList(head); cout << head << endl; deleteList(head); }
主函数中的指针head为传值调用,传到函数并没有改变主函数中的值,图示

改进的措施就是引用传值,直接操纵原指针。
