按照惯例,接下来是本篇目录:
$1 什么是最小生成树?
$2 什么是克鲁斯卡尔算法?
$3 克鲁斯卡尔算法的例题
摘要:本片讲的是最小生成树中的玄学算法--克鲁斯卡尔算法,然后就没有然后了。
$1 什么是最小生成树?
•定义:
先引入一个定理:N个点用N-1条边连接成一个联通块,形成的图形只可能是树,没有别的可能;
根据这个定理,我们定义:在一个有N个点的图中,选出N-1条边出来,连接所有N个点,这N-1条边的边权之和最小的方案;
•最小生成树之prim算法:
由于本蒟蒻还不会这个算法,所以暂时将这个算法放在这里,讲讲思路,代码实在不会打QAQ
算法思路:
1. 从图中选取一个节点作为起始节点(也是树的根节点),标记为已达;初始化所有未达节点到树的距离为到根节点的距离;
2. 从剩余未达节点中选取到树距离最短的节点i,标记为已达;更新未达节点到树的距离(如果节点到节点i的距离小于现距离,则更新);
3. 重复步骤2直到所有n个节点均为已达。
$2 什么是克鲁斯卡尔算法?
接下来是正题--克鲁斯卡尔算法
•算法思路:
(1)将所有边的边权从小到大依次排列,并且均标为未选;
(2)选择最小的未选边;
(3)如果该边与前面所选的边无法构成回路,则选中该边,并标为已选;如果该边与前面所选的边构成了回路,则不选该边,并标为已选;
(4)重复(2)(3),直到所有点之间都有边相连;
•举个栗子:
以下面这个图为例:
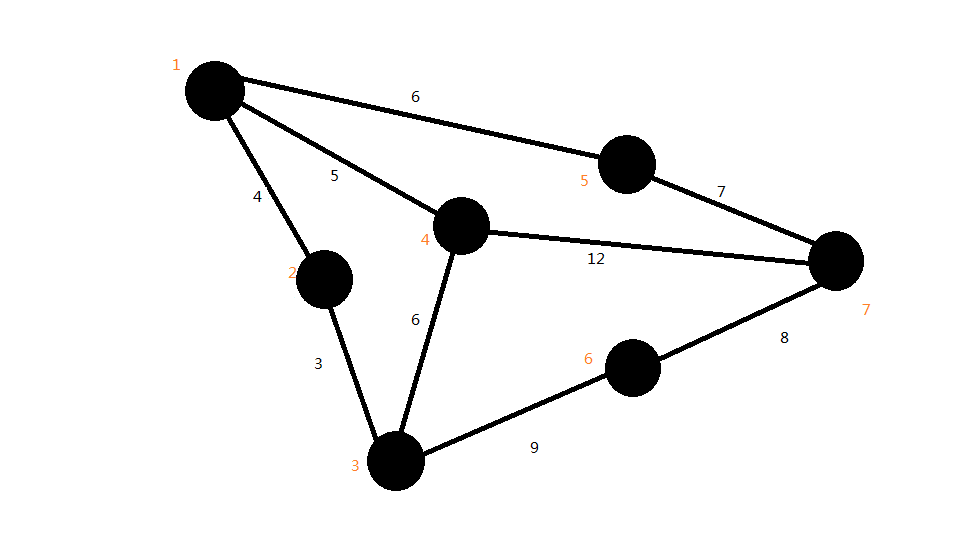
将各条边排序可得 3-4-5-6-6-7-8-9-12;
首先将最小的的边选上,即2--3,如图:
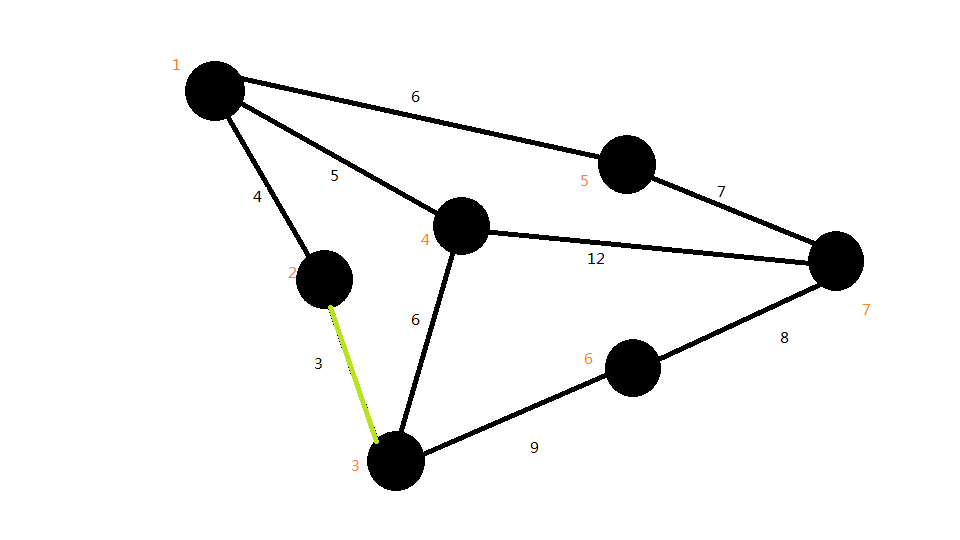
接下来,将第二条边选上,即1--2,如图:
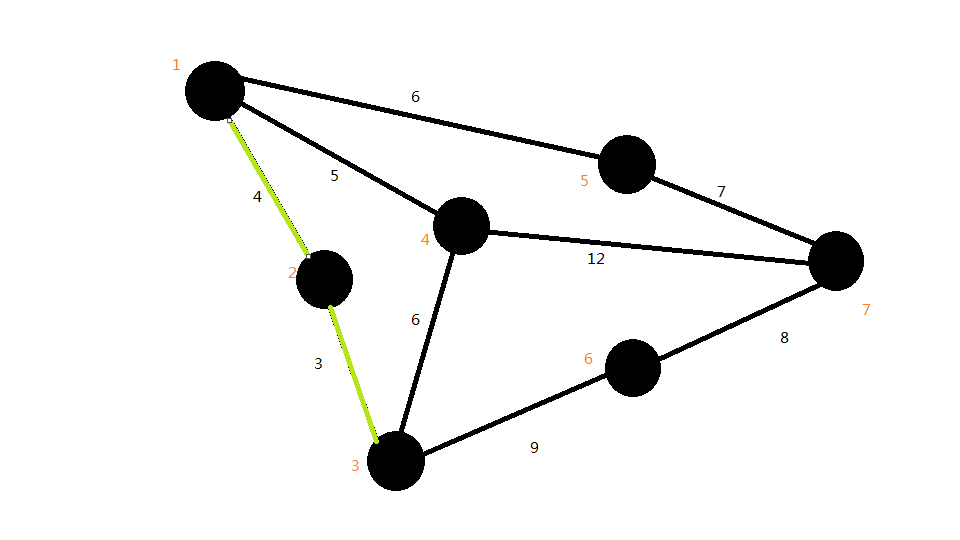
第三条边:
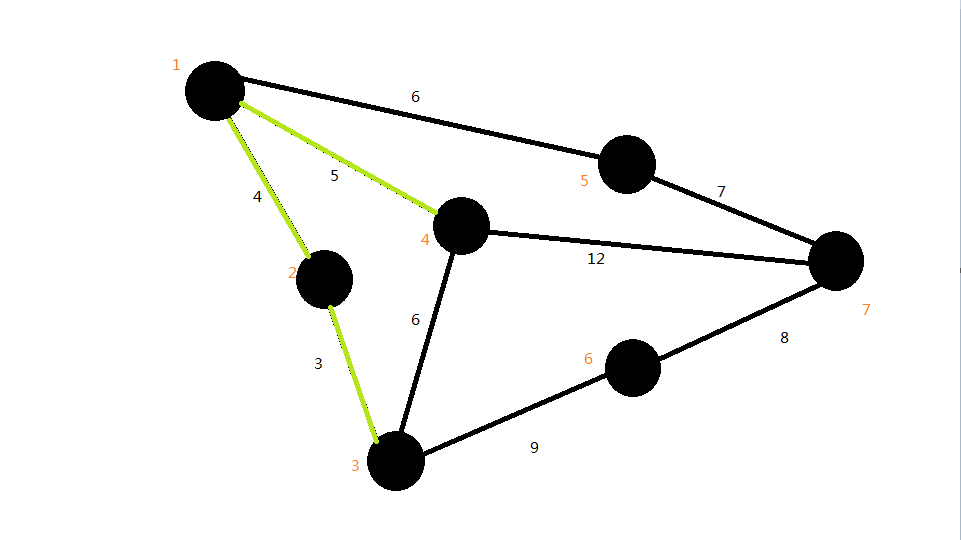
第四条边是6,但是与前三条边构成了回路,不选它;
第五条边:
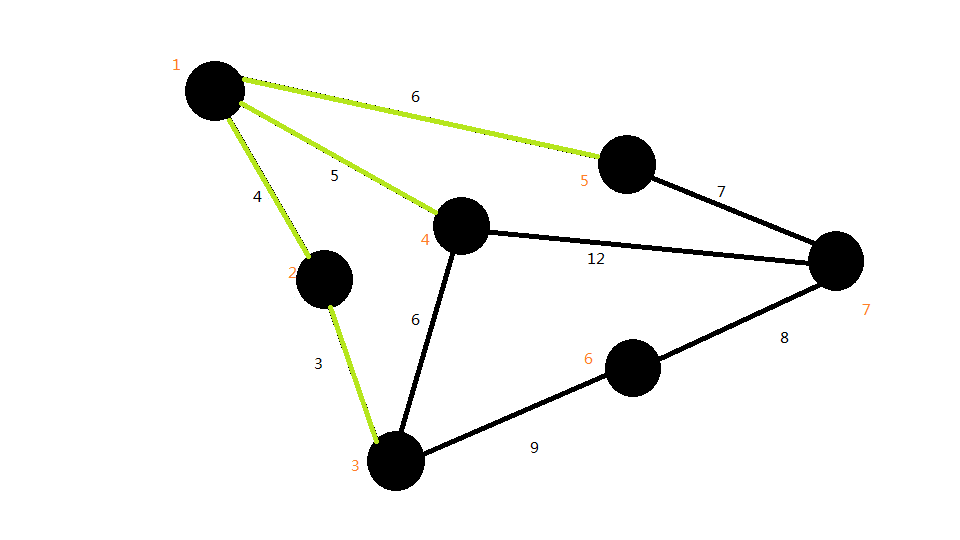
第六条边:

最后一条边:
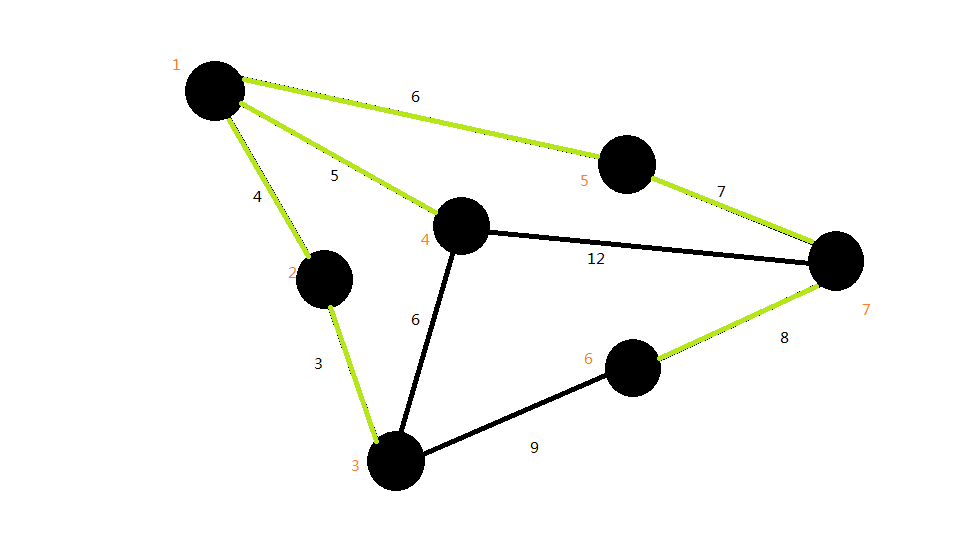
•代码实现:
1 struct point 2 { 3 int x;//始边 4 int y;//终边 5 int v;//边的权值 6 }; 7 point a[9901]; 8 int fat[101]; 9 int n,i,j,x,m,tot,k; 10 int father(int x)//并查集中的查找 11 { 12 if(fat[x]!=x) fat[x]=father(fat[x]); 13 return fat[x]; 14 } 15 16 void unionn(int x,int y)//并查集中的合并 17 { 18 int fa=father(x); 19 int fb=father(y); 20 if(fa!=fb) fat[fa]=fb; 21 } 22 23 int cmp(const point &a,const point &b) 24 { 25 if(a.v<b.v) return 1;//对边的权值进行排序 26 else return 0; 27 } 28 29 int main() 30 { 31 cin>>n; 32 for(int i=1;i<=n;++i) 33 for(int j=1;j<=n;++j) 34 { 35 cin>>x; 36 if(x!=0) 37 { 38 m++; 39 a[m].x=i;a[m].y=j;a[m].v=x; 40 } 41 } 42 for(int i=1;i<=n;++i) fat[i]=i; 43 sort(a+1,a+m+1,cmp); 44 for(int i=1;i<=m;++i) 45 { 46 if(father(a[i].x)!=father(a[i].y)) 47 { 48 unionn(a[i].x,a[i].y); 49 tot+=a[i].v; 50 k++; 51 }//如果不能构成一个联通块,就将现在的这条边加入并查集 52 if(k==n-1) break;//否则将现在的这条边撇开不管 53 } 54 cout<<tot; 55 return 0; 56 }
神仙们想必都已经看出来了,克鲁斯卡尔算法用到了并查集的思想(不会并查集的神仙戳这儿),还是很好理解的。
$3 克鲁斯卡尔算法的例题
•有且只有的一个例题: 洛谷P1546 最短网络 Agri-Net:
题目背景
农民约翰被选为他们镇的镇长!他其中一个竞选承诺就是在镇上建立起互联网,并连接到所有的农场。当然,他需要你的帮助。
题目描述
约翰已经给他的农场安排了一条高速的网络线路,他想把这条线路共享给其他农场。为了用最小的消费,他想铺设最短的光纤去连接所有的农场。
你将得到一份各农场之间连接费用的列表,你必须找出能连接所有农场并所用光纤最短的方案。每两个农场间的距离不会超过100000
输入输出格式
输入格式:
第一行: 农场的个数,N(3<=N<=100)。
第二行..结尾: 后来的行包含了一个N*N的矩阵,表示每个农场之间的距离。理论上,他们是N行,每行由N个用空格分隔的数组成,实际上,他们限制在80个字符,因此,某些行会紧接着另一些行。当然,对角线将会是0,因为不会有线路从第i个农场到它本身。
输出格式:
只有一个输出,其中包含连接到每个农场的光纤的最小长度。
输入输出样例
4
0 4 9 21
4 0 8 17
9 8 0 16
21 17 16 0
28
接下来是我懒得讲的代码(和上面一样)
1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 using namespace std; 5 struct point 6 { 7 int x; 8 int y; 9 int v; 10 }; 11 point a[9901]; 12 int fat[101]; 13 int n,i,j,x,m,tot,k; 14 int father(int x) 15 { 16 if(fat[x]!=x) fat[x]=father(fat[x]); 17 return fat[x]; 18 } 19 20 void unionn(int x,int y) 21 { 22 int fa=father(x); 23 int fb=father(y); 24 if(fa!=fb) fat[fa]=fb; 25 } 26 27 int cmp(const point &a,const point &b) 28 { 29 if(a.v<b.v) return 1; 30 else return 0; 31 } 32 33 int main() 34 { 35 cin>>n; 36 for(int i=1;i<=n;++i) 37 for(int j=1;j<=n;++j) 38 { 39 cin>>x; 40 if(x!=0) 41 { 42 m++; 43 a[m].x=i;a[m].y=j;a[m].v=x; 44 } 45 } 46 for(int i=1;i<=n;++i) fat[i]=i; 47 sort(a+1,a+m+1,cmp); 48 for(int i=1;i<=m;++i) 49 { 50 if(father(a[i].x)!=father(a[i].y)) 51 { 52 unionn(a[i].x,a[i].y); 53 tot+=a[i].v; 54 k++; 55 } 56 if(k==n-1) break; 57 } 58 cout<<tot; 59 return 0; 60 }
enddd~~