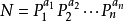屋子里有1到100号100盏关闭的灯,门外有1到100号100个人,每个人都要进屋一次,把与自己序号对应的和是自己序号倍数的灯绳拉一下,(比如1号要拉所有的灯绳,2号要拉2,4,6的灯绳,而100号只需拉100号灯绳)问:当100人都出来后,屋子里亮着的灯有几盏?
这么说呢,大家都知道答案是 平方数 1,4,9...100
ok,首先要想到肯定是拉灯拉了奇数次的才能是打开的。。。
想想如果编号为N,那么肯定是前面拉过N的i必定能整除N,所以肯定i是N的因数。。。
所以题目转换为求N,N的因数的个数是奇数。
1、只有平方数的因数是奇数,因为比如N = a*b,其中a和b不同的话,都是成对的,只有当a*a的时候,才只有一个因数,所以肯定是平方数。。。
2、来个高端大气的证明:
由唯一分解定理:p是素数,对应的a是p的指数,然后又唯一分解: 就是: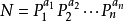
那么N的因数个数为多少呢?就是:s = (a1+1)*(a2+2)*...*(an+1),组合数学了,取出0个、1个、an个的Pn来构成。
问题转为使得因数的个数 s 为奇数。。。这里就好想了嘛,肯定只能 奇数*奇数 = 奇数 ,所以,ai+1都是奇数,所以ai都是偶数。
既然所有的ai都是偶数,那么对于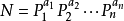 来说,不就可以把所有的ai提一个2出来么N = (P1^(a1/2) * P2^(a2/2) *...* Pn^(an/2) )^2 ,那么N就是一个完全平方数啦~~~
来说,不就可以把所有的ai提一个2出来么N = (P1^(a1/2) * P2^(a2/2) *...* Pn^(an/2) )^2 ,那么N就是一个完全平方数啦~~~
证明完毕!
来说,不就可以把所有的ai提一个2出来么N = (P1^(a1/2) * P2^(a2/2) *...* Pn^(an/2) )^2 ,那么N就是一个完全平方数啦~~~