先来看一个问题:从S点到E点有很多条路径可走,但每条路径的长短(权重)不同,且走的路径必须是S -> X1i -> X2i ->X3i ->E。求怎样走总的路径最短?
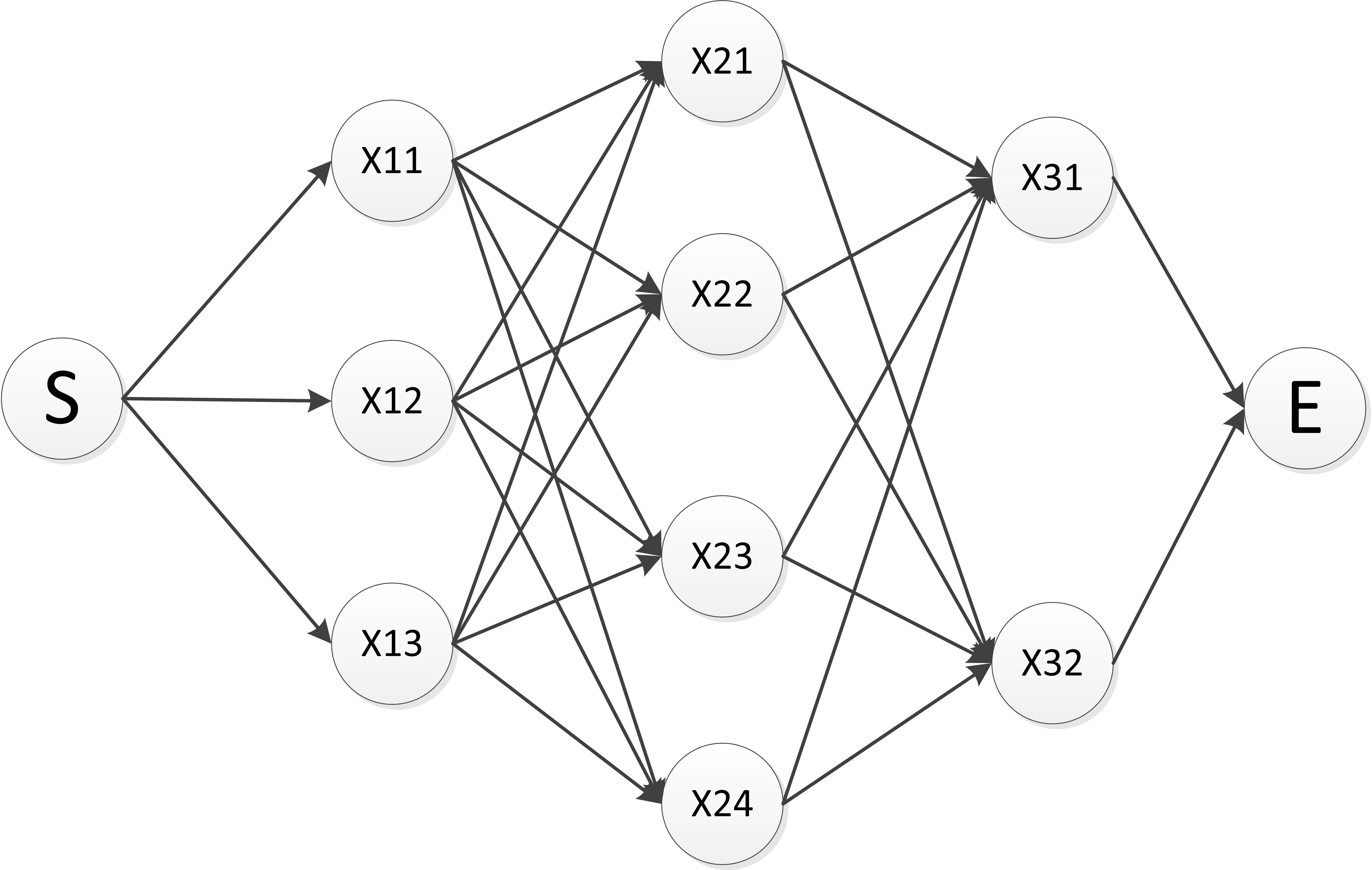
传统的方法:总的路径的条数=3*4*2=24条,分别求出每条路径的长度,然后取最短的那条路径。这种算法可以求出全局最短的路径,但时间复杂度是O(N1*N2*....),将随着问题规模的扩大而迅速增大。
贪心算法:第1步,先求出S到所有X1i的最短距离,比如说到X12最近;第2步,以第1步中得到的节点为据点,分别计算X12到X2i的距离,取距离最短的那个节点为新的据点;第3步,迭代步骤2,直到到达终点。这种算法得到的是局部最优解而非全局最优解,假设问题有Z级,所有级数中节点数最多的那一级的节点数是R,则问题的复杂度是O(Z*R)。
动态规划算法:第1步,要求S到E的最短距离,只需要先求S到X31的最短距离,比方说是P(SX31),以及S到X32的最短距离,比方说是P(SX32)。接下来我们假设X31到E点的距离是D(X31E),X32到E点的距离是D(X32E)。最后,我们比较P(SX31)+D(X31E)和P(SX32)+D(X32E)的大小,取较小的那个就是最短距离。可以用反正法证明上面的结论:假设我们上面得到最短路径是P(SX31)+D(X31E),即最短路径经过X31。如果存在另外一条路径P'(SX31),使得P'(SX31)+D(X31E) < P(SX31)+D(X31E),则P'(SX31)<P(SX31),这与P(SX31)是S到X31的最短路径相矛盾;如果存在另外一条路径P'(SX32),使得P'(SX32)+D(X32E) < P(SX31)+D(X31E),则显然有P'(SX32)+D(X32E)<P(SX31)+D(X31E)<P(SX32)+D(X32E),则P'(SX32)<P(SX32),这与P(SX3,2)是S到X32的最短路径相矛盾。这就说明了S到E的全局最短路径一定经过了S到E的上一级N个节点的全局最短路径中的某一条。总结成一句话:如果从S到E的全局最短距离经过某个节点Xij,则S到Xij这段节点的路径必定也是所有S到Xij的路径中全局最短的;
第2步,上面的第1步已经说明要求S到E的全局最短距离,只要分别求出S到E的上一级N个节点的全局最短距离,这样问题的规模就减小了1。同理,要求S到E的上一级N个节点的最小距离,需要知道S到E的上两级M个节点的最小距离,假设这个条件已知,则需要经过O(M*N)的复杂度计算得到S到E的上一级节点的最小距离。假设R=max{M,N},则计算复杂度一定小于O(R^2);
第3步,反复迭代步骤2,则问题的规模进一步减小,一直到O(R^2),变成了最初始的状态,即求S到第一级节点的最短距离。前面的分析都没有开始解决问题,现在我们可以真正开始解决问题了。我们记下S到第一级节点的最短距离,这个过程的时间复杂度为O(R^2),在求出S到第一级节点的最短距离的情况下,我们接着求S到第二级爱所有节点的最短距离,然后记下来,这个过程的时间复杂度也是O(R^2),我们依次向前推进,则求出了S到最后一级节点E的最短距离。整个算法的复杂度为O(Z*R^2),Z是整个问题的层数,R是所有级数中节点数最多的那一级的节点数。
上面的动态规划算法,被用在通信过程的解码问题上,就是维比特算法。
动态规划算法的基本要素是:最优子结构性质和重叠子问题性质