题目均来自洛谷
参考增减自:
https://www.cnblogs.com/victorique/p/8560656.html
https://blog.csdn.net/crzbulabula/article/details/56494668
方格取数 --> 最大闭合权图
看到棋盘先来一套黑白染色 黑点连s 白点连t 然后跑一遍最小割 用全部的值减去最小割即为答案
为什么呢?
想一下 最小割即为求出能连接X集和Y集所有关系的边的权和 删去这些边之后 则X集就没有边通向Y集 即消除了白点和黑点的矛盾
剩下的白点和黑点 不存在矛盾 且权和最大 因为我们删去的是最小割
拆点
1.基础拆点——入点和出点
割点:
教辅的组成
题解:本题的构图思路可以表示为:
源点->练习册->书(拆点)->答案->汇点
注意一定要拆点,因为一本书只能用一次。
看下图 这样点2就用了两次
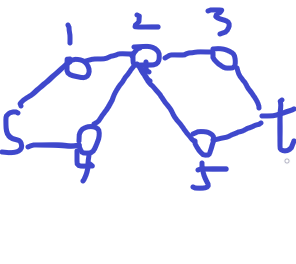
例题:奶牛的电信
为什么找这道奶牛题。。以为确实是割点的题目不是很好找,剩下的题目不大适合放在这个地方。如果你好好看了刚才的割点,这个题应该可以直接做出来了。不详述了。
2.按照时间拆点
有一部分题目是这样的,我们给出的图的同时也给出了一个天数或者时间的限制,然后对每一天做出询问,最后求总和,很明显的一点是,要把每一天都连向汇点然后求出总和。这个时候我们发现,如果其他的点仅仅只是一个点的话,无法满足求出每一天这个要求,因为会互相影响,这个时候我们就相应的把这些点拆成天数这么多个点,然后分别向向对应的天数连边。例题的话一会会有一些笔者认为比较好的题集中放在一起,这里就先介绍建图方法了。
3.根据时间段拆点
这不是和上面那个一样么???实际上不是的,注意,刚才那个是时间,而这个是时间段。不过说实话这种拆点方式主要是在费用流里出现,因为有很多这种题目,就是一个人在不同的流量是费用是不一样的,所以为了满足这个要求,就把这个人拆成一共有多少不同费用的点。举个例子:你们数学老师今天布置作业越多,你的不满值越大,如果是5张以下,一张卷子增加1点不满值,如果10张以下,一张卷子增加两点,如果10张以上,那么一张卷子增加inf点不满值。那么我们就把你拆成三个点,分别对应三种不满值
4.蛇皮拆点
有很多题目,拆点往往十分难想或者蛇皮至极有很多典型的例子就不一一详述了,比如什么一个点拆三个点四个点之类的。直接说一些例题貌似是比较好的。
[CQOI2012]交换棋子
题解:忽略图中的白色棋子,只考虑黑色棋子,问题转变成
将原图中的每个黑色棋子移动成新图的样子,最少需要移动多少步
约束是每个格子有一个经过次数的上限
把某个黑棋子,从格子A移动到格子B,视作从A流出流入B
那么就将一个点i拆成三个点,xi,yi,zi,连(xi,yi)和(yi,zi)两条边
前者用来限制流入后者限制流出
分类讨论图中的每个点(i,j),记A = (xi,yi)的容量,B = (yi,zi)的容量,交换上限为wi,j
如果原图和新图中某个位置颜色相同,说明其流入流出次数应该相等,所以A = B = wi,j / 2
如果原图是黑色而新图是白色,说明应该多流出一次,所以A = wi,j / 2,B = (wi,j + 1) / 2
反之,同理可得A = (wi,j + 1) / 2,B = wi,j / 2
上述除法全部是取下整
构建超级源S,超级汇T
如果某点在原图是黑色,连S到yi,j容量为1的边,代表这个黑棋子从这个点出发
如果某点在新图是黑色,连yi,j到T容量为1的边,代表必须有一个黑棋子在这里停止
最后,根据八连通把x,z之间的边建完,跑个最小费用最大流就行了
六、点的构造
大部分题目是有迹可循的,因为他们至少有点或者有明显能够当做点的状态。或者题目给出的点就真的能够当成点使用。但是也有的题目,并没有明显的点的提示,或者给出的你明显的点完全不能够当成网络流里的点使用。对于这种题目,我们就要自己构造出来一些新的点来进行网络流的使用。
单说可能不是很好理解,我们放上几道题给大家看一下。
[HEOI2016/TJOI2016]游戏
这题就是hdu 1045 多了一个限制 不过没事。。应该还可以用二分图去做 匈牙利跑一遍
网络流也可以
这张网格图可以抽象成一系列行块和列块,列块和行块就是说,这一个横行块或纵列块里至多放一个炸弹,另外显而易见的,我们发现选中一个点的时候会同时选中两个块,那么也就是说这张图满足两个限制条件
1.每个点最多被选中一次
2.某些点对之间有必选关系
那么之后连边跑网络流即可了。
七、动态思想
1.基本介绍
有一些题目是这个样子的,他们往往有着较其他网络流题目更大的数据,并且他们也有一个特点,就是在一部分边连好之后,之后是先建建图或者是跑一个点再加一个点这么建图对最终结果并没有影响。这样一来我们就可以通过动态加点或者边的方式使其满足题目要求的复杂度。
2.限制条件
2.1数据范围不能过大
虽说是减小了时间复杂度,但是也只是减少了部分,很多情况下复杂度的等级并没有变化,只是因为在大部分操作里减少了一些不必要的操作使速度加快。
2.2主要应用于费用流
大多时候动态加点的题目都是费用流题目,原因就是最短路一次基本上也就只能增广出来一条增广路,如果是网络流的话,当前弧优化往往能够取到更好的效果。费用流由于大部分人都会使用EK的朴素算法,所以动态加点可以是速度提高好几个档次。
2.3当前最优原则
刚才说过了前面点的选择不会影响后面的选择,这里仔细说一下。因为在跑网络流的时候,不可避免的后面跑的点回合前面跑的点有冲突,这个时候我们可以通过反边来使冲突化解。那么如果我们一个一个的加点,很明显就没办法满足这个条件。但是如果我们可以确定当前这个点跑了这个流,后面的点跑这个流的一定不如这个点优,那么我们就可以无视那个冲突了。
3.经典的例子
[NOI2012]美食节&&[SCOI2007]修车
这两个题的原理都是一样的,就是差在了一个数据范围,我们先说后面那个数据范围小的。
题目描述
同一时刻有N位车主带着他们的爱车来到了汽车维修中心。维修中心共有M位技术人员,不同的技术人员对不同的车进行维修所用的时间是不同的。现在需要安排这M位技术人员所维修的车及顺序,使得顾客平均等待的时间最小。
说明:顾客的等待时间是指从他把车送至维修中心到维修完毕所用的时间。
数据范围
(2<=M<=9,1<=N<=60), (1<=T<=1000)
Solution
要求平均时间最短,就等同于要求总时间最短
对于一个修车工先后用W1−WnW1−Wn的几个人,花费的总时间是
不难发现倒数第a个修就对总时间产生a*原时间的贡献
然后我们将每个工人划分成N个阶段,(i,t)表示修车工i在倒数第t个修
可以建一个二分图,左边表示要修理的东西,右边表示工人+阶段
于是可以从左边的e向右边的(i,t)连边,权值是Time[e][i]∗tTime[e][i]∗t,就是第e个用i这个修车工所用时间
最小权值完全匹配后,最小权值和除以N就是答案
因为权值是正的,所以一个修车工接到的连线一定是从(i,1)开始连续的,也符合现实情况
因为假设是断续的,那后面的(i,n)改连向(i,n-k),k<n时,答案更优,违背了前面的最优性
这样我们建立好图以后直接跑费用流就可以了。
那么我们继续看下一道题
题目描述 2.0
m个厨师都会制作全部的n种菜品,但对于同一菜品,不同厨师的制作时间未必相同。他将菜品用1, 2, ..., n依次编号,厨师用1, 2, ..., m依次编号,将第j个厨师制作第i种菜品的时间记为 ti,j 。小M认为:每个同学的等待时间为所有厨师开始做菜起,到自己那份菜品完成为止的时间总长度。换句话说,如果一个同学点的菜是某个厨师做的第k道菜,则他的等待时间就是这个厨师制作前k道菜的时间之和。而总等待时间为所有同学的等待时间之和。现在,小M找到了所有同学的点菜信息: 有 pi 个同学点了第i种菜品(i=1, 2, ..., n)。他想知道的是最小的总等待时间是多少。
数据范围 2.0
对于100%的数据,n <= 40, m <= 100, p <= 800, ti,j <= 1000 (其中p = ∑pi)
Solution 2.0
连边还是和上一个题目一样。那么数据范围变大了,我们现在的时间复杂度就是O(n2m×p×k¯¯¯n2m×p×k¯)嗯,T了。
那么怎么办呢?通过仔细的思考可以发现,我们观察发现,第一次spfa得出的最短路肯定是某人倒数第一个修某车某厨师倒数第一个做某菜,因为倒数第一个肯定比倒数第二个距离短
那么我们可以在一开始建图的时候,只把所有“倒数第一个做的菜”的那些边加上
一旦一条增广路被用掉了(也就是一个厨师-做菜顺序二元组(j,k) 被用掉了),那么我们就把所有代表二元组(j,k+1) 加上去(一共有n条),再跑spfa
这样我们图中的总边数不会超过n∗∑ni=1p[i]n∗∑i=1np[i]
也就是总时间在O(np2∗k¯¯¯)O(np2∗k¯)左右,k是spfa常数,就可以通过这道题。
8.最大密度子图
这个事实上都可以单独拿来当成一个题做了。先说一下要求:
给定一个无向图,要求从无向图里抽出一个子图,使得子图中的边数∣E∣∣E∣与点数∣V∣∣V∣的比值最大,即求最大的∣E∣∣V∣∣E∣∣V∣.
给出一种解法,由前面说过的最大权闭合子图得到的。假设答案为k ,则要求解的问题是:选出一个合适的点集 V 和边集 E,令(|E|−k∗|V|)取得最大值。所谓“合适”是指满足如下限制:若选择某条边,则必选择其两端点。
建图:以原图的边作为左侧顶点,权值为1;原图的点作为右侧顶点,权值为 −k (相当于 支出 kk)。 若原图中存在边 (u,v),则新图中添加两条边 ([uv]−>u), ([uv]−>v),转换为最大权闭合子图。 其中k可以二分得到。
锅,突然发现这个东西没证。。。。
然后发现第一步并不能证出来。。。
现在我又证出来了。。。
无向图的子图的密度:D=|E||V|D=|E||V|
看成是分数规划问题,二分答案 λ ,需要求
g(λ)=max(|E|−λ|V|)g(λ)=max(|E|−λ|V|)
g(λ)=0时我们取到最优解。
喏,现在权当我这一步证出来了。
给出证明吧。
给出函数λ=f(x)=a(x)b(x)(x∈S)λ=f(x)=a(x)b(x)(x∈S)
那么我们猜测一个最优值λ,重新构造一个函数:
g(λ)=max{a(x)−λb(x)}g(λ)=max{a(x)−λb(x)}
若我们设一个λ∗=f(x∗)λ∗=f(x∗)为最优解,那么则有:
g(λ)<0⇔λ>λ∗g(λ)<0⇔λ>λ∗
g(λ)=0⇔λ=λ∗g(λ)=0⇔λ=λ∗
g(λ)>0⇔λ<λ∗g(λ)>0⇔λ<λ∗
似乎貌似就是大于小于的情况要么不合法,要么不够优。当g(λ)=0时正好取到最优解。
然后我们开始思考如何搞出来,可以发现我们选择一条边就要选择与它相连的两个端点。那么,随便YY一下,搞一个如上面的建图,就可以发现上面那个建图满足我们的条件。
可是有个问题,当λ取到一定值的时候,它变大并不会影响最大权闭合图的值,统统都是0.。所以我们二分求得是在g(λ)=0时最小的λ。
11.最长反链和最小链覆盖
在有向无环图中,链是一个点的集合,这个集合中任意两个元素v、u,要么v能走到u,要么u能走到v。
反链是一个点的集合,这个集合中任意两点谁也不能走到谁。
最长反链是反链中最长的那个。
那怎么求呢?
11.1 传递闭包
在开始介绍这个之前,我先简单叙述一下传递闭包是个什么东西。可以发现的是百度百科里的东西都奇怪的一批根本让人看不懂。那么我就尽量通俗的说一下。
传递闭包就是求一个图里面所有满足传递性的点。那么传递性又是什么呢?简单来说就是:假设图中对于图中的节点ii,若果有一个j点可以到ii,ii点又可以到kk,那么jj就能到kk。这样的节点就可以说是有传递性。看上去非常的,简单。其实就是这样。求完传递闭包之后,我们能够知道的是图中的任意两点是否相连。
那么,我们可以用Floyd算法搞出来,没错,就是Floyd。只不过我们现在是求两点是否相连,而不是求其最短路径。
11.2最小链覆盖
这个东西就是求出最长反链的关键。因为:最小链覆盖=最长反链长度。
那么,最小链覆盖又怎么求出呢?
回想一下我们之前是不是有一个地方介绍过了最小路径覆盖。那个地方所求的是不能相交的最小路径覆盖,那么这里我们要求的就是路径可以相交的最小路径覆盖。
问题又来了,这个又怎么求解呢?
我们把原来的图做一遍传递闭包,然后如果任意两点x,yx,y,满足xx可以到达yy,那么我们就在拆点后的二分图里面连一条(x1,y2)(x1,y2)的边。
这样球可以绕过一些在原图中被其他路径占用的点,构造新的路径从而求出最小路径覆盖。
那么这样我们就把可以相交的最小路径覆盖转化为了路径不能相交的最小路径覆盖了。 从而我们求出了这个图的最小链覆盖。
11.3 十分感性的证明
那么我们证明一下刚才一个结论的正确性。
我们通过观察定义可以得出,最长反链的点一定在不同的链里。所以最长反链长度≤≤最小链覆盖数。
那么我们接着可以通过感性理解和数学归纳证出最长反链长度≥≥最小链覆盖数.
如此我们就能够得证了。
11.4最长链长度 = 最小反链覆盖数
不想证了。这个结论就是上面的反向结论,其实直接背过就可以了。。。。。