《Java算法》Java动态规划

1. 算法思想：

动态规划(dynamic programming)是运筹学的一个分支，是求解决策过程(decision process)最优化的数学方法。
动态规划实际上是一类题目的总称，并不是指某个固定的算法。动态规划的意义就是通过采用递推（或者分而治之）的策略，通过解决大问题的子问题从而解决整体的做法。动态规划的核心思想是巧妙的将问题拆分成多个子问题，通过计算子问题而得到整体问题的解。而子问题又可以拆分成更多的子问题，从而用类似递推迭代的方法解决要求的问题。

2. 应用场景：
适用动态规划的问题必须满足最优化原理、无后效性和重叠性。
1.最优化原理（最优子结构性质） 最优化原理可这样阐述：一个最优化策略具有这样的性质，不论过去状态和决策如何，对前面的决策所形成的状态而言，余下的诸决策必须构成最优策略。简而言之，一个最优化策略的子策略总是最优的。一个问题满足最优化原理又称其具有最优子结构性质。
2.无后效性 将各阶段按照一定的次序排列好之后，对于某个给定的阶段状态，它以前各阶段的状态无法直接影响它未来的决策，而只能通过当前的这个状态。换句话说，每个状态都是过去历史的一个完整总结。这就是无后向性，又称为无后效性。
3.子问题的重叠性 动态规划将原来具有指数级时间复杂度的搜索算法改进成了具有多项式时间复杂度的算法。其中的关键在于解决冗余，这是动态规划算法的根本目的。动态规划实质上是一种以空间换时间的技术，它在实现的过程中，不得不存储产生过程中的各种状态，所以它的空间复杂度要大于其它的算法。

3. 案例分析

题目：数塔

从上走到下，求经过的数字和的最大值

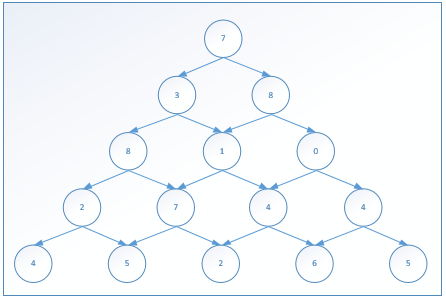
解题思路：

从底部开始，先通过小三角求解：

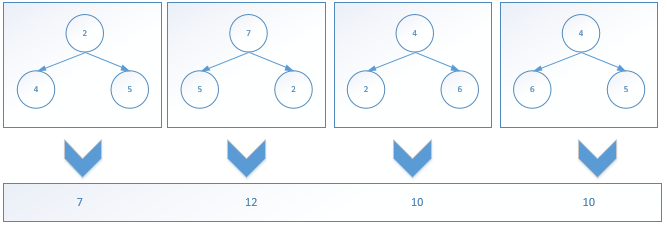
计算每一个小三角，经过的数字和的最大值。 并且将他们记录下来，后面继续使用

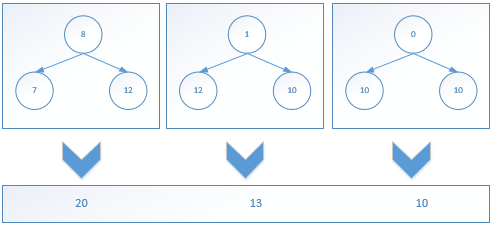
一直下去，直到计算到顶部。

 ....

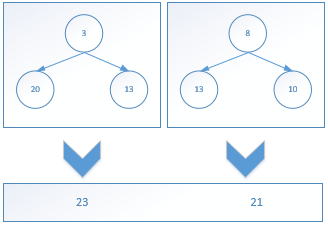
代码如下：

public class dp {
    public static void main(String[] args) {
        int[][] arr = {
                    {7, 0, 0, 0, 0},
                  {3, 8, 0, 0, 0},
                {8, 1, 0, 0, 0},
              {2, 7, 4, 4, 0},
            {4, 5, 2, 6, 5}
        };
        System.out.println(new dp().maxSumNew(arr));
    }

    /**
     * 动态规划
     * @param arr
     * @param
     * @return
     */
    public int maxSumNew(int[][] arr) {
        if (arr == null) {
            return 0;
        }
        int n = arr.length;
        int[][] max = new int[n][n];
        for (int i = n - 1; i >= 0; i--) {
            for (int j = 0; j <= i; j++) {
                if (i == n - 1) {
                    max[n - 1][j] = arr[n - 1][j];
                } else {
                    max[i][j] = Math.max(max[i + 1][j], max[i + 1][j + 1]) + arr[i][j];
                }
            }
        }
        return max[0][0];
    }
}

运行结果：

总结：最优化原理、无后效性和重叠性，有该特性的题目就可以考虑动态规划。