Chomsky文法类型判断（Recognizing the type of the Chomsky grammar）

1.试验目的

输入：一组任意的规则。

输出：相应的Chomsky 文法的类型。

2.实验原理

1)．0型文法（短语文法）

如果对于某文法G，P中的每个规则具有下列形式：

   u:: = v

其中u∈V^＋，v∈V^*，则称该文法G为0型文法或短语文法，简写为PSG。

0型文法或短语结构文法的相应语言称为0型语言或短语结构语言L₀。这种文法由于没有其他任何限制，因此0型文法也称为无限制文法，其相应的语言称为无限制性语言。任何0型语言都是递归可枚举的，故0型语言又称递归可枚举集。这种语言可由图灵机（Turning）来识别。

2)．1型文法（上下文有关文法）

如果对于某文法G，P中的每个规则具有下列形式：

   xUy:: = xuy

其中U∈V_N；u∈V^＋；x，y∈V^*，则称该文法G为1型文法或上下文有关文法，也称上下文敏感文法，简写为CSG。

1型文法的规则左部的U和右部的u具有相同的上文x和下文y，利用该规则进行推导时，要用u替换U，必须在前面有x和后面有y的情况下才能进行，显示了上下文有关的特性。

1型文法所确定的语言为1型语言L₁，1型语言可由线性有界自动机来识别。

  

3)．2型文法（上下文无关文法）

如果对于某文法G，P中的每个规则具有下列形式：

   U :: = u

其中U∈V_N；u∈V^＋，则称该文法G为2型文法或上下文无关文法，简写为CFG。

按照这条规则，对于上下文无关文法，利用该规则进行推导时，无需考虑非终结符U所在的上下文，总能用u替换U，或者将u归约为U，显示了上下文无关的特点。

2型文法所确定的语言为2型语言L₂，2型语言可由非确定的下推自动机来识别。

一般定义程序设计语言的文法是上下文无关的。如C语言便是如此。因此，上下文无关文法及相应语言引起了人们较大的兴趣与重视。

4)．3型文法（正则文法，线性文法）

如果对于某文法G，P中的每个规则具有下列形式：

   U :: = T  或  U :: = WT

其中T∈V_T；U,W∈V_N，则称该文法G为左线性文法。

如果对于某文法G，P中的每个规则具有下列形式：

   U :: = T  或  U :: = TW

其中T∈V_T；U, W∈V_N，则称该文法G为右线性文法。

左线性文法和右线性文法通称为3型文法或正则文法，有时又称为有穷状态文法，简写为RG。

按照定义，对于正则文法应用规则时，单个非终结符号只能被替换为单个终结符号，或被替换为单个非终结符号加上单个终结符号，或者被替换为单个终结符号加上单个非终结符号。

3型文法所确定的语言为3型语言L₃，3型语言可由确定的有限状态自动机来识别。

在常见的程序设计语言中，多数与词法有关的文法属于3型文法。

可以看出，上述4类文法，从0型到3型，产生式限制越来越强，其后一类都是前一类的子集，而描述语言的功能越来越弱，四类文法及其表示的语言之间的关系可表示为：

0型1型2型3型；即L₀ L₁ L₂ L₃

3..实验内容

1）输入一组文法规则，以S为开始符，大写字母为非终结符，非大写字母为终结符。

2）判断文法类型并生成文法的四元组形式。

3）输出文法类型及文法。

4.实验心得

这次实验让我体会到了判别文法的复杂性，我的算法是先默认是正则文法，再依次判断，而许多同学是每次对一条规则进行相同的判断，我认为这是可以改进的，例如若发现上一条规则是符合1型文法，则当前的规则就只需从1型文法开始判断，详见源代码。

5.实验代码与结果

1)源代码

/********************************************************************
created:    2013/05/28
created:    28:5:2013   20:15
file base:  main
file ext:   cpp
author:     Justme0 (http://blog.csdn.net/Justme0)

purpose:
判断文法类型。
输入约定以S为开始符，大写字母为非终结符，非大写字母为终结符。

*********************************************************************/

#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <string>
#include <vector>
#include <set>
#include <algorithm>
#include <cassert>
using namespace std;

const int STRING_MAX_LENGTH = 10;

/*
** 一条规则
*/
struct Principle {
    string left;
    string right;

    Principle(const char *l, const char *r) : left(l), right(r) {}
};

/*
** 文法的四元组形式，同时将该文法类型也作为其属性
*/
struct Grammer {
    set<char> Vn;
    set<char> Vt;
    vector<Principle> P;
    char S;

    int flag;    // 文法类型

    Grammer(void) : flag(-1) {}
};


/*
** 输入规则
*/
void input(vector<Principle> &principleSet) {
    char left[STRING_MAX_LENGTH];
    char right[STRING_MAX_LENGTH];
    while (EOF != scanf("%[^-]->%s", left, right)) {
        getchar();
        principleSet.push_back(Principle(left, right));
    }
}

/*
** 得到S, Vn, Vt
*/
void getGrammer(Grammer &G) {
    G.S = G.P.front().left.front();
    G.Vn.clear();
    G.Vt.clear();

    for (unsigned i = 0; i < G.P.size(); ++i) {
        const Principle &prcp = G.P[i];

        for (unsigned j = 0; j < prcp.left.size(); ++j) {
            char v = prcp.left[j];
            !isupper(v) ? G.Vt.insert(v) : G.Vn.insert(v);
        }
        for (unsigned j = 0; j < prcp.right.size(); ++j) {
            char v = prcp.right[j];
            !isupper(v) ? G.Vt.insert(v) : G.Vn.insert(v);
        }
    }
}

/*
** 判断字符串（文法的左部）中是否存在一个非终结符。
*/
bool hasUpper(string s) {
    return s.end() != find_if(s.begin(), s.end(), isupper);
}

/*
** 判断文法类型。
*/
void check(int &flag, const Principle &prcp) 
{
    switch (flag) {
    case 3:
        if (
            1 == prcp.left.size() && isupper(prcp.left.front()) &&
            (1 == prcp.right.size() && !isupper(prcp.right.front()) ||
            2 == prcp.right.size() && !isupper(prcp.right.front()) && isupper(prcp.right.back()))
            ) {
                break;
        }

    case 2:
        if (1 == prcp.left.size() && isupper(prcp.left.front())) {
            flag = 2;
            break;
        }

    case 1:
        if (hasUpper(prcp.left) && prcp.left.size() <= prcp.right.size()) {
            flag = 1;
            break;
        }

    default :
        // 所有的文法规则左部都必须至少含有一个非终结符，是否应放到最前面判断？
        // 用异常机制exit是否合适？
        try {
            if (!hasUpper(prcp.left)) {
                throw exception("输入的文法错误！");
            }
        } catch (exception e) {
            cout << e.what() << endl;
            exit(-1);
        }

        flag = 0;
        break;
    }
}


/*
** 判别文法并生成四元组形式。
*/
void solve(Grammer &G) {
    G.flag = 3;    // 从正则文法开始判断
    for (unsigned i = 0; i < G.P.size(); ++i) {
        check(G.flag, G.P[i]);
    }
    getGrammer(G);
}

/*
** 输出文法
*/
void output(const Grammer &G) {
    cout << "G = (Vn, Vt, P, S)是" << G.flag << "型文法\n" << endl;

    cout << "Vn:" << endl;
    for (auto ite = G.Vn.begin(); ite != G.Vn.end(); ++ite) {
        cout << *ite << endl;
    }
    cout << endl;

    cout << "Vt:" << endl;
    for (auto ite = G.Vt.begin(); ite != G.Vt.end(); ++ite) {
        cout << *ite << endl;
    }
    cout << endl;

    cout << "P:" << endl;
    for (auto ite = G.P.begin(); ite != G.P.end(); ++ite) {
        cout << (*ite).left << "->" << (*ite).right << endl;
    }
    cout << endl;

    cout << "S:\n" << G.S << endl;
};

int main(int argc, char **argv) {
    freopen("cin.txt", "r", stdin);

    Grammer G;
    input(G.P);
    solve(G);
    output(G);

    return 0;
}

 

2)实验结果

（1）

输入：

S->aSBE

S->aBE

EB->BE

aB->ab

bB->bb

bE->be

eE->ee

输出：

 

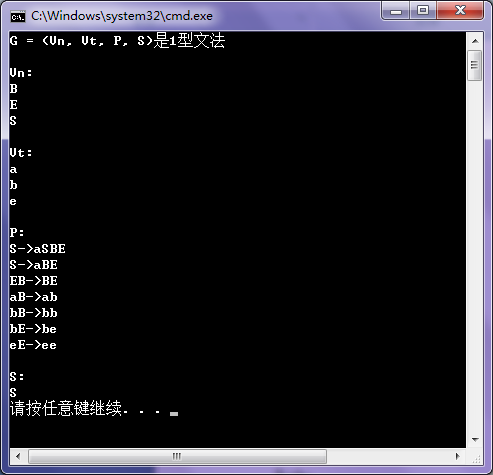
（2）

输入：

S->aB

S->bA

A->a

A->aS

A->bAA

B->b

B->bS

B->aBB

输出：