41. 包含min函数的栈
设计一个支持push,pop,top等操作并且可以在O(1)时间内检索出最小元素的堆栈。
push(x)–将元素x插入栈中
pop()–移除栈顶元素
top()–得到栈顶元素
getMin()–得到栈中最小元素
样例
MinStack minStack = new MinStack();
minStack.push(-1);
minStack.push(3);
minStack.push(-4);
minStack.getMin(); --> Returns -4.
minStack.pop();
minStack.top(); --> Returns 3.
minStack.getMin(); --> Returns -1.
思路: 可以用两个栈,一个是正常的栈,另一个栈存储每个状态栈内最小的元素。
#include<bits/stdc++.h>
using namespace std;
class MinStack {
public:
/** initialize your data structure here. */
stack<int> num;
stack<int> Min;
MinStack() {
}
void push(int x) {
num.push(x);
if (Min.empty() || Min.top() >= x)
Min.push(x);
else Min.push(Min.top());
}
void pop() {
Min.pop();
num.pop();
}
int top() {
return num.top();
}
int getMin() {
return Min.top();
}
};
/**
* Your MinStack object will be instantiated and called as such:
* MinStack obj = new MinStack();
* obj.push(x);
* obj.pop();
* int param_3 = obj.top();
* int param_4 = obj.getMin();
*/
128. 编辑器
你将要实现一个功能强大的整数序列编辑器。
在开始时,序列是空的。
编辑器共有五种指令,如下:
1、“I x”,在光标处插入数值x。
2、“D”,将光标前面的第一个元素删除,如果前面没有元素,则忽略此操作。
3、“L”,将光标向左移动,跳过一个元素,如果左边没有元素,则忽略此操作。
4、“R”,将光标向右移动,跳过一个元素,如果右边没有元素,则忽略次操作。
5、“Q k”,假设此刻光标之前的序列为a1,a2,…,an,输出max1≤i≤kSi,其中Si=a1+a2+…+ai。
输入格式
第一行包含一个整数Q,表示指令的总数。
接下来Q行,每行一个指令,具体指令格式如题目描述。
输出格式
每一个“Q k”指令,输出一个整数作为结果,每个结果占一行。
数据范围
1≤Q≤106,
|x|≤103,
1≤k≤n
输入样例:
8
I 2
I -1
I 1
Q 3
L
D
R
Q 2
输出样例:
2
3
思路: 前4个操作可以通过栈顶栈来模拟。操作5可以用数组Sum[i]记录1i的前缀,Max[i]记录1i最大的前缀,如果删除一个值,只对当前光标后面的sum和Max有影响,每次所以当右移光标时,都计算一遍当前点的Sum和Max.
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+5;
typedef long long LL;
stack<int> a,b;
LL pre[maxn],Max[maxn];
int main(){
int N,x,flag=0;
char ch;
cin>>N;
Max[0]=-100000000,pre[0]=0;
while(N--){
cin>>ch;
//cout<<ch<<endl;
if(ch=='I'){
cin>>x;
a.push(x);
flag++;
pre[flag]=pre[flag-1]+x;
Max[flag]=max(pre[flag],Max[flag-1]);
}
else if(ch=='D'){
if(!a.empty()){
a.pop();
flag--;
}
}
else if(ch=='L'){
if(!a.empty()){
b.push(a.top());
a.pop();
flag--;
}
}
else if(ch=='R'){
if(!b.empty()){
a.push(b.top());
b.pop();
flag++;
pre[flag]=pre[flag-1]+a.top();
Max[flag]=max(Max[flag-1],pre[flag]);
}
}
else if(ch=='Q'){
cin>>x;
cout<<Max[x]<<'
';
}
}
return 0;
}
129. 火车进栈
这里有n列火车将要进站再出站,但是,每列火车只有1节,那就是车头。
这n列火车按1到n的顺序从东方左转进站,这个车站是南北方向的,它虽然无限长,只可惜是一个死胡同,而且站台只有一条股道,火车只能倒着从西方出去,而且每列火车必须进站,先进后出。
也就是说这个火车站其实就相当于一个栈,每次可以让右侧头火车进栈,或者让栈顶火车出站。
车站示意如图:
出站<—— <——进站
|车|
|站|
|__|
现在请你按《字典序》输出前20种可能的出栈方案。
输入格式
输入一个整数n,代表火车数量。
输出格式
按照《字典序》输出前20种答案,每行一种,不要空格。
数据范围
1≤n≤20
输入样例:
3
输出样例:
123
132
213
231
321
思路: 考虑三个状态是三个栈,考虑字典序后就是先从火车站出站,再进站。可以写个消除影响的dfs。
#include<bits/stdc++.h>
using namespace std;
const int N=21;
vector<int> state1;
stack<int> state2;
int state3=0;
int n,cnt=20;
void dfs(){
if(!cnt){
return ;
}
if(state1.size()==n){
for(auto t: state1) cout<<t;
cout<<'
';
--cnt;
return ;
}
if(state2.size()){//出
state1.push_back(state2.top());
state2.pop();
dfs();
state2.push(state1.back());
state1.pop_back();
}
if(state3!=n){//进
state3++;
state2.push(state3);
dfs();
state2.pop();
state3--;
}
}
int main(){
cin>>n;
dfs();
return 0;
}
达达是一名漫画家,她有一个奇特的爱好,就是在纸上画括号。
这一天,刚刚起床的达达画了一排括号序列,其中包含小括号( )、中括号[ ]和大括号{ },总长度为N。
这排随意绘制的括号序列显得杂乱无章,于是达达定义了什么样的括号序列是美观的:
(1) 空的括号序列是美观的;
(2) 若括号序列A是美观的,则括号序列 (A)、[A]、{A} 也是美观的;
(3) 若括号序列A、B都是美观的,则括号序列AB也是美观的。
例如 (){} 是美观的括号序列,而)({)[}]( 则不是。
现在达达想在她绘制的括号序列中,找出其中连续的一段,满足这段子序列是美观的,并且长度尽量大。
你能帮帮她吗?
输入格式
输入一行由括号组成的字符串。
输出格式
输出一个整数,表示最长的美观的子段的长度。
数据范围
字符串长度不超过100000。
输入样例:
({({(({()}})}{())})})[){{{([)()((()]]}])[{)]}{[}{)
输出样例:
4
思路: 最长括号序列的升级问题。从前向后匹配,每次将括号和下标都存入栈中(只存下标更好),当发生一个非法括号后,将栈清空,再继续匹配,当匹配成功的一对要在改对记录数组上做标记。最后统计数组中最长连续被标记子段的长度。
#include<bits/stdc++.h>
using namespace std;
const int N=100010;
typedef pair<char,int> PCI;
char s[N];
int pos[N];
stack<PCI> sk;
int vis[N];
bool check(int i){
if(s[i]==')'||s[i]=='}'||s[i]==']'){
return true;
}
return false;
}
bool isok(char c1,char c2){
if(c1=='['&&c2==']') return true;
if(c1=='{'&&c2=='}') return true;
if(c1=='('&&c2==')') return true;
return false;
}
void clear(){
while(!sk.empty())
sk.pop();
}
int main(){
cin>>s;
int flag=0;
for(int i=0;s[i];++i){
if(!check(i)){
sk.push({s[i],i});
}
else if(sk.empty()&&check(i)){
continue;
}
else if(check(i)){
if(isok(sk.top().first,s[i])){
pos[sk.top().second]=++flag;
pos[i]=flag;
//cout<<sk.top().second<<" "<<i<<endl;
sk.pop();
}
else {
clear();
}
}
}
int n=strlen(s),len=0,ans=0;
for(int i=0;i<n;++i){
if(pos[i]!=0){
len++;
}
else len=0;
ans=max(ans,len);
}
cout<<ans<<endl;
return 0;
}
给出一个表达式,其中运算符仅包含+,-,*,/,^(加 减 乘 整除 乘方)要求求出表达式的最终值。
数据可能会出现括号情况,还有可能出现多余括号情况。
数据保证不会出现大于或等于231的答案。
数据可能会出现负数情况。
输入格式
输入仅一行,即为表达式。
输出格式
输出仅一行,既为表达式算出的结果。
输入样例:
(2+2)^(1+1)
输出样例:
16
思路:
将中序表达式转化为后缀表达式,步骤:
1.当是数字时,放到数字栈中,注意判断前面的负号表示意义是负号还是减号。
2.当是左括号加入栈中
3.当前运算符的运算优先级不大于栈顶元素,则将栈顶运算符弹出,参与计算,最后将当前运算符放到栈顶,降序栈。(优先级*,/,^ > +,- > (,) )
4.当是右括号时,依次弹出栈顶元素参与计算,直到弹出左括号
最后将栈内没弹出的运算符弹出计算
#include<bits/stdc++.h>
using namespace std;
string a;
stack<char> s;
stack<double> is;
int gl(char c){
if(c=='+'||c=='-') return 1;
if(c=='*'||c=='/'||c=='^') return 2;
if(c=='(') return 0;
}
void calc(char c){
if(c=='(') return ;
double num1=is.top();
if(is.size()>1)
is.pop();
else return ;
double num2=is.top();is.pop();
if(c=='-')
is.push(num2-num1);
if(c=='+')
is.push(num1+num2);
if(c=='*')
is.push(num1*num2);
if(c=='/')
is.push(num2/num1);
if(c=='^'){
is.push(pow(num2,num1));
}
}
int main(){
cin>>a;
for(int i=0;i<a.size();++i){
char c=a[i];
bool f=0;
if(c=='-'){
if(i==0||a[i-1]=='(') f=1;
}
if((c>='0'&&c<='9')||f) {
int tmp=0,s=1;
if(f) s=-1,++i;
c=a[i];
while(c>='0'&&c<='9'){
tmp=tmp*10+c-'0';
++i;
c=a[i];
}
--i;
is.push(tmp*s);
}
else {
if(c=='(')
s.push('(');
else if(c==')'){
while(!s.empty()&&s.top()!='('){
calc(s.top());
s.pop();
}
if(!s.empty())
s.pop();
}
else if(!s.empty()){
if(gl(c)>gl(s.top())){
s.push(c);
}
else {
while(!s.empty()&&gl(c)<=gl(s.top())){
calc(s.top());
s.pop();
}
s.push(c);
}
}
else {
s.push(c);
}
}
}
while(!s.empty()){
calc(s.top());
s.pop();
}
cout<<is.top()<<endl;
return 0;
}
131. 直方图中最大的矩形
直方图是由在公共基线处对齐的一系列矩形组成的多边形。
矩形具有相等的宽度,但可以具有不同的高度。
例如,图例左侧显示了由高度为2,1,4,5,1,3,3的矩形组成的直方图,矩形的宽度都为1:
通常,直方图用于表示离散分布,例如,文本中字符的频率。
现在,请你计算在公共基线处对齐的直方图中最大矩形的面积。
图例右图显示了所描绘直方图的最大对齐矩形。
输入格式
输入包含几个测试用例。
每个测试用例占据一行,用以描述一个直方图,并以整数n开始,表示组成直方图的矩形数目。
然后跟随n个整数h1,…,hn。
这些数字以从左到右的顺序表示直方图的各个矩形的高度。
每个矩形的宽度为1。
同行数字用空格隔开。
当输入用例为n=0时,结束输入,且该用例不用考虑。
输出格式
对于每一个测试用例,输出一个整数,代表指定直方图中最大矩形的区域面积。
每个数据占一行。
请注意,此矩形必须在公共基线处对齐。
数据范围
1≤n≤100000,
0≤hi≤1000000000
输入样例:
7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0
输出样例:
8
4000
思路: 要组合成最大的矩形,可以微调证明高度必然等于某个长方形的高度。对于每一个长方形,可以以它的高度组合成的矩形的方法是找到它左右相邻所有不必它矮的矩形,如果它前面的一个矩形比他矮,那么对于前面所有的矩形的高度都和它没有关系了。所以可以用单调栈,当栈顶小于它的高度,就将栈顶弹出,由于栈内是递增的,所以它是栈顶遇到的第一个矮于栈顶的长方形,所以弹出时统计一下可延展的最大下标是i-1或i+1,这样左右个遍历各一边,最后统计最大面积。
#include<bits/stdc++.h>
using namespace std;
const int N=100001;
struct node{
int h,l,r;
}p[N];
int n;
stack<int> sk;
int main(){
while(cin>>n&&n){
for(int i=1;i<=n;++i)
cin>>p[i].h;
while(!sk.empty()){
sk.pop();
}
for(int i=1;i<=n;++i){
if(sk.empty()||p[sk.top()].h<=p[i].h){
sk.push(i);
continue;
}
while(!sk.empty()&&p[sk.top()].h>p[i].h){
int t=sk.top();
sk.pop();
p[t].r=i-1;
}
sk.push(i);
}
while(!sk.empty()){
int t=sk.top();
sk.pop();
p[t].r=n;
}
for(int i=n;i>=1;--i){
if(sk.empty()||p[sk.top()].h<=p[i].h){
sk.push(i);
continue;
}
while(!sk.empty()&&p[sk.top()].h>p[i].h){
int t=sk.top();
sk.pop();
p[t].l=i+1;
}
sk.push(i);
}
while(!sk.empty()){
int t=sk.top();
sk.pop();
p[t].l=1;
}
long long ans=0;
for(int i=1;i<=n;++i){
ans=max(ans,1ll*(p[i].r-p[i].l+1)*p[i].h);
}
cout<<ans<<'
';
}
return 0;
}
152. 城市游戏
有一天,小猫rainbow和freda来到了湘西张家界的天门山玉蟾宫,玉蟾宫宫主蓝兔盛情地款待了它们,并赐予它们一片土地。
这片土地被分成NM个格子,每个格子里写着’R’或者’F’,R代表这块土地被赐予了rainbow,F代表这块土地被赐予了freda。
现在freda要在这里卖萌。。。它要找一块矩形土地,要求这片土地都标着’F’并且面积最大。
但是rainbow和freda的OI水平都弱爆了,找不出这块土地,而蓝兔也想看freda卖萌(她显然是不会编程的……),所以它们决定,如果你找到的土地面积为S,它们将给你3S两银子。
输入格式
第一行包括两个整数N,M,表示矩形土地有N行M列。
接下来N行,每行M个用空格隔开的字符’F’或’R’,描述了矩形土地。
每行末尾没有多余空格。
输出格式
输出一个整数,表示你能得到多少银子,即(3*最大’F’矩形土地面积)的值。
数据范围
1≤N,M≤1000
输入样例:
5 6
R F F F F F
F F F F F F
R R R F F F
F F F F F F
F F F F F F
输出样例:
45
思路: 我们可以通过枚举1~m为地面(代码写成纵向当作地面的),构造出上一题的模型,枚举O(m),每次单调队列O(n),总复杂度:O(nm).
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
char g[N][N];
int p[N],n,m;
stack<int> q;
int l[N],r[N];
int solve(){
while(!q.empty()){
q.pop();
}
for(int i=0;i<n;++i){
if(!q.empty()){
while(!q.empty()&&p[q.top()]>p[i]){
r[q.top()]=i-1;
q.pop();
}
}
q.push(i);
}
while(!q.empty()){
r[q.top()]=n-1;
q.pop();
}
for(int i=n-1;i>=0;--i){
if(!q.empty()){
while(!q.empty()&&p[q.top()]>p[i]){
l[q.top()]=i+1;
q.pop();
}
}
q.push(i);
}
while(!q.empty()){
l[q.top()]=0;
q.pop();
}
int ans=0;
for(int i=0;i<n;++i){
ans=max(ans,(r[i]-l[i]+1)*p[i]);
}
return ans;
}
int main(){
cin>>n>>m;
for(int i=0;i<n;++i)
for(int j=0;j<m;++j)
cin>>g[i][j];
int ans=0;
for(int j=0;j<m;++j){
for(int i=0;i<n;++i){
if(g[i][j]=='F') p[i]++;
else p[i]=0;
}
ans=max(ans,solve());
}
cout<<ans*3<<'
';
return 0;
}
153. 双栈排序
Tom最近在研究一个有趣的排序问题。
通过2个栈S1和S2,Tom希望借助以下4种操作实现将输入序列升序排序。
操作a
如果输入序列不为空,将第一个元素压入栈S1
操作b
如果栈S1不为空,将S1栈顶元素弹出至输出序列
操作c
如果输入序列不为空,将第一个元素压入栈S2
操作d
如果栈S2不为空,将S2栈顶元素弹出至输出序列
如果一个1~n的排列P可以通过一系列操作使得输出序列为1, 2,…,(n-1), n,Tom就称P是一个”可双栈排序排列”。
例如(1, 3, 2, 4)就是一个”可双栈排序序列”,而(2, 3, 4, 1)不是。
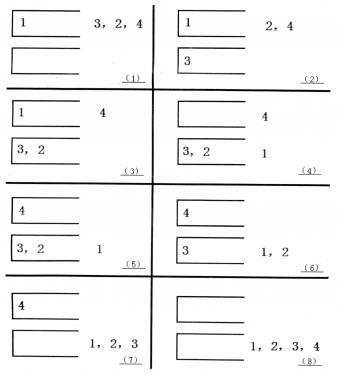
下图描述了一个将(1, 3, 2, 4)排序的操作序列:<a, c, c, b, a, d, d, b>
当然,这样的操作序列有可能有几个,对于上例(1, 3, 2, 4),<a, c, c, b, a, d, d, b>是另外一个可行的操作序列。
Tom希望知道其中字典序最小的操作序列是什么。
输入格式
第一行是一个整数n。
第二行有n个用空格隔开的正整数,构成一个1-n的排列。
输出格式
输出共一行,如果输入的排列不是”可双栈排序排列”,输出数字0。
否则输出字典序最小的操作序列,每两个操作之间用空格隔开,行尾没有空格。
数据范围
1≤n≤1000
输入样例:
4
1 3 2 4
输出样例:
a b a a b b a b
思路: 当可以确定每个数字能进入S1还是S2栈,就可以确定唯一的一个最小字典序操作序列了。对于本题有一个重要的性质:(a_k<a_i<a_j) 且(i<j<k),ai和aj不能放到同一个栈中。可以反证法证明:若能ai,aj放入同一栈,由于ak在后面,ak不进栈再出栈ai就没法出栈,但ai要在aj进栈前出栈,所以就矛盾了。
所以可以将ai,aj连边,构造出一个二分图,分别属于不同栈,最后求出每个图包含的点,知道所属栈就可以直接模拟了。由于按字典序,所以遍历时优先考虑是S1的元素,模拟时先对S1操作,再对S2操作。
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int a[N];
int g[N][N],col[N],f[N],n;
bool dfs(int u,int c){
col[u]=c;
for(int i=1;i<=n;++i){
if(g[u][i]==0) continue;
if(col[i]==col[u]) return false;
if(col[i]==-1&&!dfs(i,!c)) return false;
}
return true;
}
int main(){
int T;
cin>>n;
memset(col,-1,sizeof col);
memset(g,0,sizeof g);
for(int i=1;i<=n;++i)
cin>>a[i];
f[n+1]=n+1;
for(int i=n;i>0;--i)
f[i]=min(f[i+1],a[i]);
for(int i=1;i<=n;++i){
for(int j=i+1;j<=n;++j){
if(a[i]<a[j]&&a[i]>f[j+1]){
g[i][j]=g[j][i]=1;
}
}
}
bool flag=0;
for(int i=1;i<=n;++i){
if(col[i]==-1&&!dfs(i,0)){
flag=1;
break;
}
}
if(flag){
cout<<"0
";
return 0;
}
stack<int> sk1,sk2;
int now=1;
for(int i=1;i<=n;++i){
if(col[i]==0){
sk1.push(a[i]);
cout<<"a ";
}
if(col[i]==1){
sk2.push(a[i]);
cout<<"c ";
}
while(true){
if(!sk1.empty()&&sk1.top()==now){
sk1.pop();
cout<<"b ";
now++;
}
else if(!sk2.empty()&&sk2.top()==now){
sk2.pop();
cout<<"d ";
now++;
}
else break;
}
}
cout<<endl;
return 0;
}