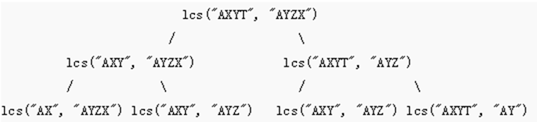首先来看什么是最长公共子序列:给定两个序列,找到两个序列中均存在的最长公共子序列的长度。子序列需要以相关的顺序呈现,但不必连续。例如,“abc”, “abg”, “bdf”, “aeg”, ‘”acefg”等都是“abcdefg”的子序列。因此,一个长度为n的序列拥有2^n中可能的子序列(序列中的每一个元素只有选或者不选两种可能,因此是2^n)。
Example:
LCS for input Sequences “ABCDGH” and “AEDFHR” is “ADH” of length 3.
LCS for input Sequences “AGGTAB” and “GXTXAYB” is “GTAB” of length 4.
该问题最普通的解法是对两个给定序列分别生成所有子序列,然后找到最长的匹配的子序列。这样的解法是指数复杂度的,显然不是我们需要的。我们来看该问题是如何拥有动态规划问题的重要性质的。
1 Optimal Substructure:
假设输入序列分别为长度为m的X[0..m-1]和长度为n的Y[0..n-1],令L(X[0..m-1], Y[0..n-1])为序列X、Y的最长公共子序列的长度,如下为L(X[0..m-1], Y[0..n-1])的递归定义:
If last characters of both sequences match (or X[m-1] == Y[n-1]) then
L(X[0..m-1], Y[0..n-1]) = 1 + L(X[0..m-2], Y[0..n-2])
If last characters of both sequences do not match (or X[m-1] != Y[n-1]) then
L(X[0..m-1], Y[0..n-1]) = MAX ( L(X[0..m-2], Y[0..n-1]), L(X[0..m-1], Y[0..n-2])
例子:
1) Consider the input strings “AGGTAB” and “GXTXAYB”. Last characters match for the strings. So length of LCS can be written as:
L(“AGGTAB”, “GXTXAYB”) = 1 + L(“AGGTA”, “GXTXAY”)
2) Consider the input strings “ABCDGH” and “AEDFHR. Last characters do not match for the strings. So length of LCS can be written as:
L(“ABCDGH”, “AEDFHR”) = MAX ( L(“ABCDG”, “AEDFHR”), L(“ABCDGH”, “AEDFH”) )
因此,LCS问题具有最优子结构性质,可以使用求解子问题的方案来解决。
2 Overlapping Subproblems:
如下是LCS问题的递归求解程序,该实现遵循了上面的递归结构:
/* A Naive recursive implementation of LCS problem */
#include<stdio.h>
#include<stdlib.h>
int max(int a, int b);
/* Returns length of LCS for X[0..m-1], Y[0..n-1] */
int lcs( char *X, char *Y, int m, int n )
{
if (m == 0 || n == 0)
return 0;
if (X[m-1] == Y[n-1])
return 1 + lcs(X, Y, m-1, n-1);
else
return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n));
}
/* Utility function to get max of 2 integers */
int max(int a, int b)
{
return (a > b)? a : b;
}
/* Driver program to test above function */
int main()
{
char X[] = "AGGTAB";
char Y[] = "GXTXAYB";
int m = strlen(X);
int n = strlen(Y);
printf("Length of LCS is %d
", lcs( X, Y, m, n ) );
getchar();
return 0;
}
以上程序的时间复杂度在最坏情况下是O(2^n),最坏情况是X与Y中的所有字符均不匹配,也就是说LCS的长度为0。
根据上面的实现,如下是当输入序列为“AXYT”和“AYZX”时的部分递归树:
不难发现,lcs(“AXY”, “AYZ”) 被计算了2次。如果我们画出完整的递归树,会找到更多被重复计算的子问题。因此,该问题具备重叠子结构性质,可以通过Memoization或者Tabulation来避免重复计算。下面是LCS问题的Tabulation实现。
/* Dynamic Programming implementation of LCS problem */
#include<stdio.h>
#include<stdlib.h>
int max(int a, int b);
/* Returns length of LCS for X[0..m-1], Y[0..n-1] */
int lcs( char *X, char *Y, int m, int n )
{
int L[m+1][n+1];
int i, j;
/* Following steps build L[m+1][n+1] in bottom up fashion. Note
that L[i][j] contains length of LCS of X[0..i-1] and Y[0..j-1] */
for (i=0; i<=m; i++)
{
for (j=0; j<=n; j++)
{
if (i == 0 || j == 0)
L[i][j] = 0;
else if (X[i-1] == Y[j-1])
L[i][j] = L[i-1][j-1] + 1;
else
L[i][j] = max(L[i-1][j], L[i][j-1]);
}
}
/* L[m][n] contains length of LCS for X[0..n-1] and Y[0..m-1] */
return L[m][n];
}
/* Utility function to get max of 2 integers */
int max(int a, int b)
{
return (a > b)? a : b;
}
/* Driver program to test above function */
int main()
{
char X[] = "AGGTAB";
char Y[] = "GXTXAYB";
int m = strlen(X);
int n = strlen(Y);
printf("Length of LCS is %d
", lcs( X, Y, m, n ) );
getchar();
return 0;
}
以上实现的时间复杂度为O(mn),相比原始递归求解的最坏情况要好太多了。
上面的程序只是返回了LCS的长度,可以参照该文章来打印LCS Printing Longest Common Subsequence 。