本文主要分机器学习和深度学习两部分介绍,介绍常用的优化算法。优化算法的重要性是不言而喻的,优化算法决定了损失函数的收敛速度,甚至是损失函数是否容易收敛,是否会收敛在最小值处(全局优化)。
机器学习优化算法
1、梯度下降法
梯度下降法可以说是机器学习中最常用的算法,当然在深度学习中也会使用。不过一般使用的都是梯度下降法的变体—小批量梯度下降法,因为在样本较大时使用全样本进行梯度下降时需要计算的梯度太多,导致计算量会非常大。梯度下降法是一种迭代算法,选取合适的初值$x^{(0)}$,不断的迭代更新$x$的值,进行目标函数$f(x) $的极小化,直至目标函数收敛。由于负梯度方向是使得函数值下降最快的方向,因此在迭代的每一步,以负梯度方向更新$x $的值,从而达到减小函数值的目的。
对于梯度下降法存在很多缺点:
1)对于非完全凸函数极容易陷入局部最优
2)对于大数据集时计算量很大
3)在接近最优区域时收敛速度非常慢,因为此时的梯度非常小
4)学习率难以自适应,通常变学习率要由于恒定的学习率。一般前期要加速下降,后期要抑制振荡。
对于梯度下降法的这些缺点,在机器学习中最常见的处理方式就是随机梯度下降(随机抽取一个样本,用其求梯度并作为本次下降的梯度,但一般随机梯度下降很难收敛到最小值),或者小批量梯度下降(从样本中取小批量来求梯度,用平均值来作为本次的梯度下降)。在深度学习中有更多的变种,这个后面再说。
2、牛顿法
同样考虑无约束优化问题minxf(x),其中f(x)是在RD上具有二阶连续偏导的函数。假设第k次迭代值为x(k),则根据目标函数的性质,我们可以将f(x)在x(k)的领域处进行二阶泰勒展开:
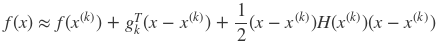
其中gk = g(x(k)) =∇f(x(k))为f(x)在x(k)的梯度,H(x(k))是f(x)的海塞矩阵(Hesse matrix) ,表达式为
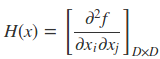
对于二次函数求极小值可以通过偏导为零来求得(当海森矩阵是正定矩阵时,f(x) 的极值就是极小值)
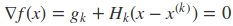
这样在第K + 1步时的最优解
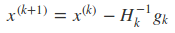
这种在领域内进行二次展开,并不断的通过求领域里的极小值来进行下降的方法就叫做牛顿法
牛顿法的下降速度会优于梯度下降法,牛顿法在领域内是用二次曲面去拟合真实的局部曲面,而梯度下降法是用平面去拟合,因此牛顿法的结果是更接近真实值的。而且牛顿法还利用了二阶导数信息把握了梯度变化的趋势,使得能够预测到下一步最优的方向,因此牛顿法比梯度下降法的预见性更远(梯度下降法每次都是从当前位置选择坡度最大的方向走,牛顿法不仅会考虑当前坡度是否最大,还会考虑之后的坡度是否最大),更能把握正确的搜索方向而加快收敛。
当然牛顿法也有很多缺点:
1)目标优化函数必须是二阶可导,海森矩阵必须正定
2)计算量太大,除了计算梯度之外,还要计算海森矩阵以及其逆矩阵
3)当目标函数不是完全的凸函数时,容易陷入鞍点。
3、拟牛顿法
拟牛顿法旨在解决牛顿法中的海森矩阵的问题。在你牛顿法中考虑用一个D阶的正定矩阵来近似的代替海森矩阵的逆矩阵。这样就避免要去计算逆矩阵。
将x = x(k+1) 代入到下面的式子中
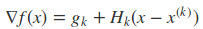
可以得到

上式即为Hk满足的条件,称为拟牛顿条件。若将Gk作为H−1k的近似,则要求Gk满足同样的条件。而在每次迭代中,可以选择更新矩阵Gk+1:
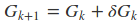
不同的Gk 的选择,就衍生出了不同的方法,常见的有DFP算法、BFGS算法(最流行的拟牛顿法)等。
深度学习
深度学习中有很多对梯度下降法的变体算法,都是用来加速神经网络的优化的(神经网络中数据量太大了,计算量太,优化慢)
4、momentum动量法
如果把梯度下降法想象成一个小球从山坡到山谷的过程,那么之前的梯度下降法的小球是这样移动的:从A点开始,计算当前A点的坡度,沿着坡度最大的方向走一段路,停下到B。在B点再看一看周围坡度最大的地方,沿着这个坡度方向走一段路,再停下。而一个真正的小球要比这聪明多了,从A点滚动到B点的时候,小球带有一定的初速度,在当前初速度下继续加速下降,小球会越滚越快,更快的奔向谷底。momentum 动量法就是模拟这一过程来加速神经网络的优化的。动量法可以认为是利用了物体的惯性来加速下行。
我们以一张图来看这个问题

因此参数更新是这样的
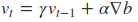
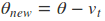
在这里的$v_{t-1}$表示之前所有步骤积累的动量,$gamma$ 是动量的衰减值,通常取0.9
5、NAG算法
NAG算法其实和动量法差不多,不同的在于动量法是将动量和当前梯度合并在一起得到另一个下降的路径。而在NAG算法中是先假定按照当前动量走一段路程然后停止,再沿着当前的梯度下降。用图表示如下
算法流程如下
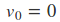
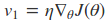
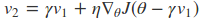
主要是是注意当前的位置是$ heta - gamma v_1$。
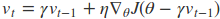

在这里$gamma$代表衰减率,通常取0.9,$eta$代表学习率。
6、Adagrad算法
Adagrad算法主要是控制学习速率的变化,让学习速率去自适应当前的环境。学习速率会在一开始比较大,当靠近最优点时,学习速率会变的很小,慢慢的去收敛到最小值。
传统的梯度下降法可以这样表示
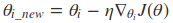
Adagrad算法的表示形式是这样的
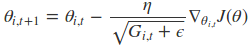
学习速率除以了一个会逐渐增大的数,并且为了确保这个除数不为0,引入了一个极小值$epsilon$,在这里注意到,参数中引入了一个$i$值,这个值表示第$i$个参数,也就是说每个参数的更新梯度都不一样,这主要是因为有些特征只出现在少部分数据中,这些特征在迭代更新的过程中可能会出现有些轮次不会更新,那么这些特征在遇到更新的时候,其学习速率应该要比较大,这样才能确保他们会和其他特征一起去收敛。
在这里$G_{i, t}$表示之前$t $步的梯度的累加,而且针对每个参数所对应的$G_{i, t}$值不一样,所以Adagrad算法不仅可以控制学习速率的变化,还可以控制每个参数的学习率的大小。
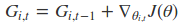
简化成向量的形式
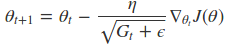
7、Adadelta算法
细心的同学可能会发现在Adagrad算法中随着$t $值的增大,$G_{i, t}会越来越大,因为在Adagrad中是将所有的历史梯度都相加在一起,这当迭代到一定次数时,就会是很大的一个值,导致后面梯度下降的很慢。因此提出了Adadelta算法,其表述形式如下

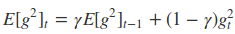
动态平均值$E{[g^2]}_t$仅仅取决于当前的梯度值与上一时刻的平均值($E{[g^2]}_{t-1}$ 表示历史梯度平方的均值),在这里采用的滑动加权平均,这样就只会和当前比较近的梯度关系比较大。
8、RMSprop算法
RMSprop算法也是一种旨在控制学习速率在后期过小的问题

9、Adam算法
Adam算法是RMSprop算法结合动量方法来实现的一种优化算法,Adam优化算法可以说是动量法和Adagrad算法的结合体,在这里提出的一阶矩和二阶矩,一阶矩可以看作是动量法的实现,二阶矩可以看作是adagrade算法的实现,主要是为了控制学习速率的变化。
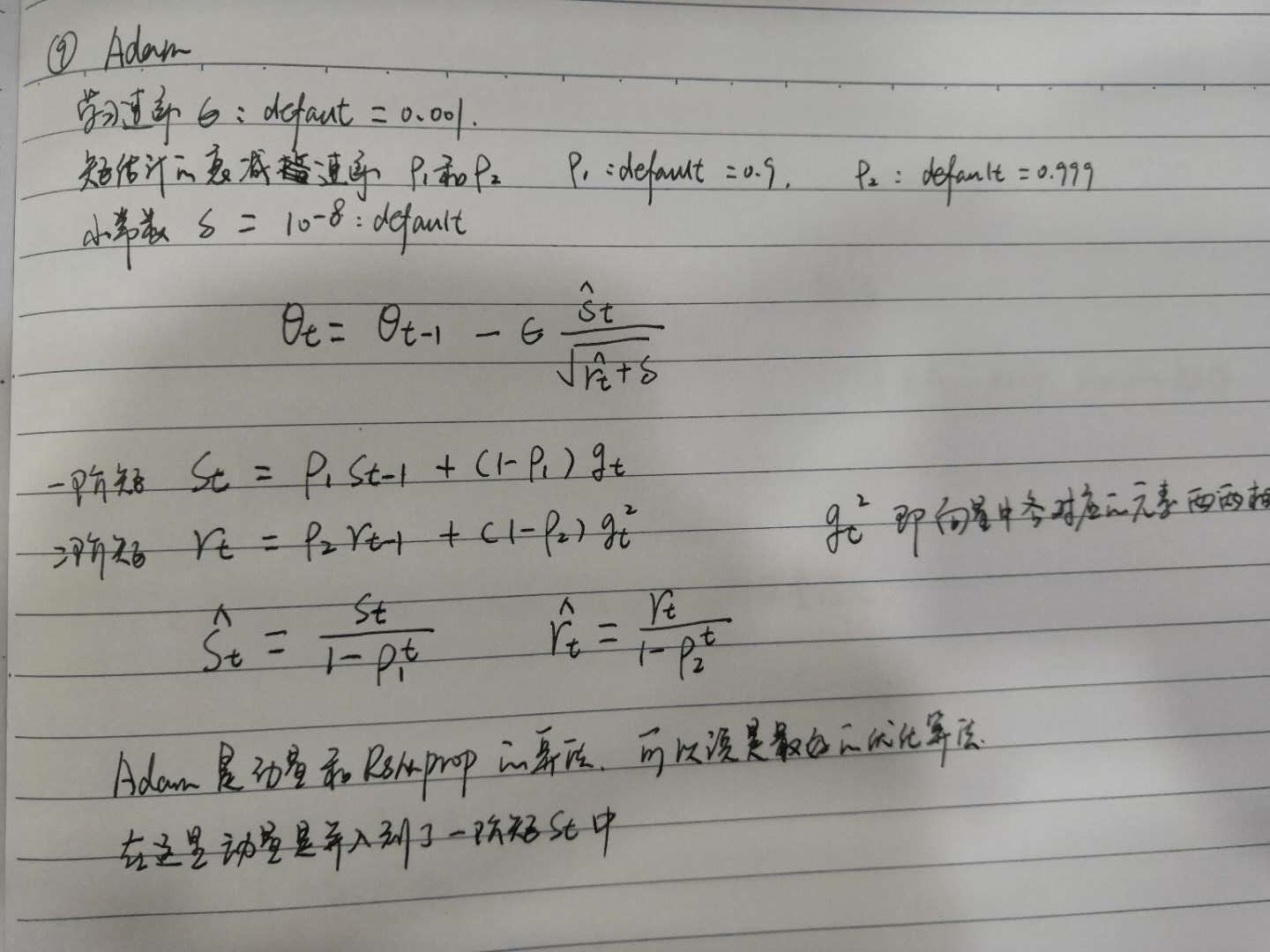
从上图中的公式可以看出,一阶矩和二阶矩都采用了缩放的指数移动加权平均法来求值。