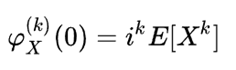统计学中特征函数理解和学习

在概率论中，特征函数的益处体现在：

1. 任意分布与它的特征函数一一对应；
2. 两个独立随机变量之和的特征函数就是它们二者特征函数的积；
3. 特征函数在零点附近收敛 == 分布函数弱收敛(Levi continuous theroem)，要处理多个独立随机变量之和的分布，可以采取以下方式：

如果随机变量各阶矩都存在，特征函数在0处求k阶导数可得到：

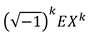
因此，特征函数是随机变量的分布的不同表示形式。

对于随机变量X的分布，用概率密度函数来描述：

 

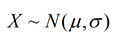
对应的概率密度函数如下：

 

概率密度函数可以直观描述随机变量 X 的分布，特征函数也可以从另一个角度描述这个分布。

特征（一个女博士为例）

 

• 名字
• 血型
• 身高
• 声音
• 打扮
• ……..

以上特征如果都一样，那么：

所有特征都相等 ==> 上述两幅图像是同一个人

根据泰勒级数可知，两个函数f(x), g(x)的各阶导数相等的越多，那么这两个函数越相似：

各阶倒数都相等 ==> f(x) = g(x)

随机变量分布的特征

• 期望µ
• 方差σ²
• 偏态SKewness
• 峰态Kurtosis
• ……..

期望：

 

方差：

 

偏态：

 

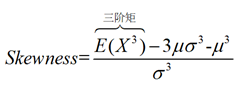
可见特征都可由各阶矩计算得出，直觉上可以有以下推论（其实还是有条件的，这里先忽略这些严格性，在实际应用中如下思考问题不大）：

各阶矩相等 ==> 各特征相等 ==> 分布相同

特征函数

随机变量X的特征函数定义为：

 

泰勒级数展开：

 

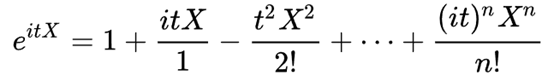
因此，可得：

 

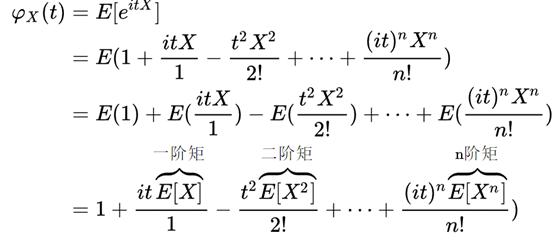
原来特征函数包含了分布函数的所有矩，也就是包含了分布函数的所有特征。

 

所以，特征函数其实是随机变量X的分布的另外一种描述方式。

特征函数是共轭傅立叶变换

 

可见两者是共轭的关系：

 

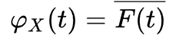
也就是说，特征函数是f(x)的共轭傅立叶变化，以下将特征函数当作傅立叶变换来理解。

特征函数相当于换了一个坐标系

直角坐标系下，圆的方程为： 

 

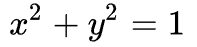
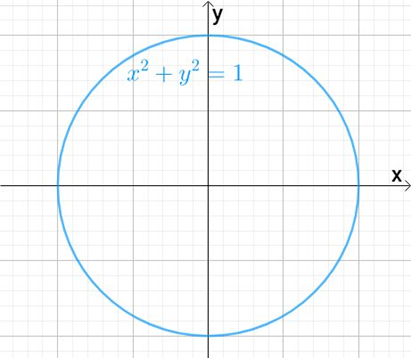
在极坐标系下，同样的圆的方程为：

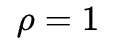
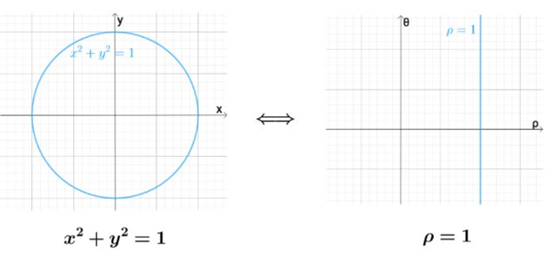
同一个数学对象，在不同坐标系中，有不同的表达形式：

傅立叶变换和直角坐标、极坐标的情况类似，相当于换了坐标系。

矩形波在时域“坐标系”中的形状：

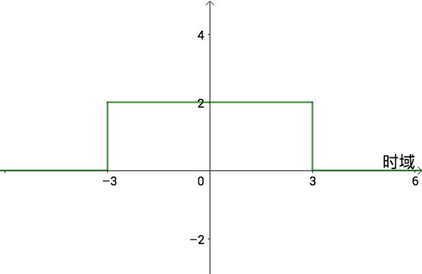
代数形式如下：

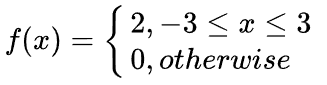
在频域“坐标系”中的图像如下：

 

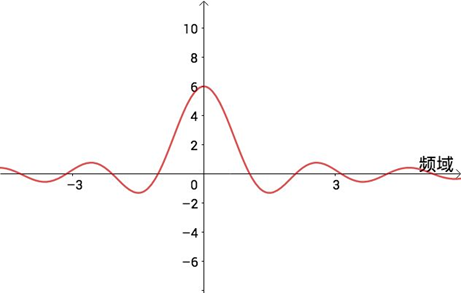
代数形式如下：

 

也是同一个数学对象，在不同“坐标系”中，有不同的表达方式：

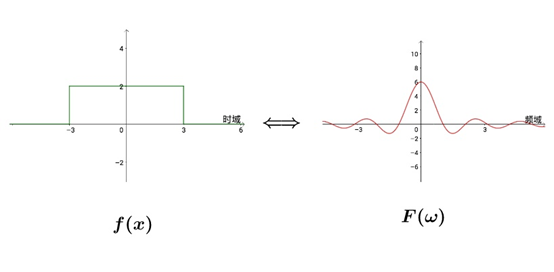
所以，特征函数是把分布函数换了一个坐标系，因此是分布函数的另外一种表现形式：

特征函数的好处：

正如把直角坐标系换到极坐标系，可以获得计算上的便利。

特征函数把分布函数换到另外一个坐标系，也可以获得一些计算的好处：

（1）假如不知道分布函数，但是通过实验计算出了期望、方差、偏度、峰度等特征，那么可以用特征函数去代替分布函数；

（2）两个分布函数的卷积：

 

通过特征函数更换坐标系后，可以变为更容易计算的乘法：

 

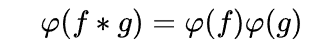
通过对 t 求导，可以简单求出各阶矩：