69. x 的平方根

第一眼想到的思路是迭代，必然存在 res*res<x<(res+1)*(res+1),这样的话在n^0.5的时间内可以处理好，

于是有以下代码

public int mySqrt(int x) {
        int res = 0;
　　　　 // 必然存在 res*res<x<(res+1)*(res+1)
        while((res*res)<=x){
            res++;
        }
　　　　  // 题目求的是向下取整，所以这里需要-1来中和上面的res++
        return res-1;
    }

测试了几个样例都没问题，但是在x=2147395600时却报错了

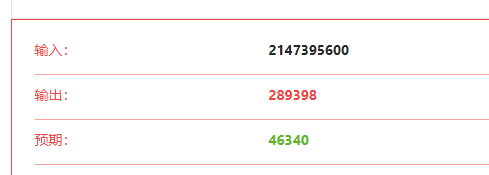
这个数值非常接近于Integer.MAX_VALUE了，也就是int的最大值

所以这里出现了一个漏洞，就是res=46340时，res*res<x，但是此时继续res++就导致了res*res>Integer.MAX_VALUE

于是变出现了溢出，res*res变为了负数，自然就小于x了。于是这里我们做出如下改动

public int mySqrt(int x) {
        int res = 0;
        while((res*res)<x){
            res++;
        }
　　　　　// (res+1)*(res+1)未溢出前必然大于x,否则就是溢出的情况
        return res*res>x ? res-1:res;
    }

测试样例可得出正确结果，很可惜的是超时了

我们做下优化，这次采用二分的办法来一点点逼近近似值

public int mySqrt(int x) {
        int res = 0,left=1,right=x,mid=0;
        while(left<=right){
            // 避免溢出，将(left+right)/2改为left+(right-left)/2
            mid = left+(right-left)/2;
            // 同样，避免溢出，
            if ((long)mid*mid<=x) {
                res = mid;
                left = mid+1;
            }else{
                right=mid-1;
            }
        }
        return res;
    }

使用二分查找那我们可以很轻松的得出O(logx)的时间复杂度

查了一下有牛顿法可以解决，时间复杂度也是O(logx)，但是要更收敛，所以比二分法要更快一点

涉及到斜率的知识，可惜社畜已经把数学知识忘光了，

只能参考下别人的解答了