动手动脑java作业

1.程序截图

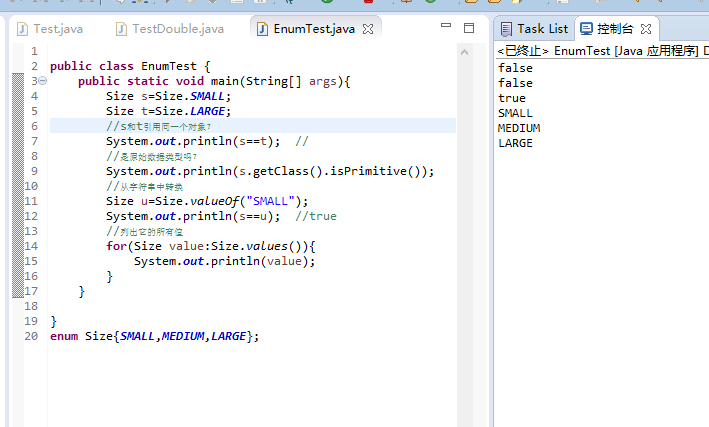
第一个false：判断s和t里的值，不同则输出false

第二个false：当且仅当这个类表示一个基本类型此方法返回true

第三个true：判断s和u里的值，相同则输出true

最后则是列出Size的所有值。

其中的问题：

//s和t引用同一个对象？不是

//是原始数据类型吗？不是

2.计算机的原码、补码和反码：

1.原码：原码表示法是机器数的一种简单的表示法。其符号位用 0表示正号，用1表示负号，数值一般用二进制形式表示。

2.补码：机器数的补码可由原码得到。如果机器数是正数，则该机器数的补码与原码一样；如果机器数是负数，则该机器数的补码是对它的原码（除符号位外）各位取反，并在未位加1而得到 的。

3.反码：机器数的反码可由原码得到。如果机器数是正数，则该机器数的反码与原码一样；如果机器数是负数，则该机器数的反码是对它的原码（符号位除外）各位取反而得到的。

例如：[X1] = +1010110（二进制）

[X1] 原= 01010110

[X1] 补= 01010110

[X1]反 = 01010110

[X2] = -1001010（二进制）

[X2]原 = 11001010

[X2] 补= 10110110

[X2] 反= 10110101 

3.同名变量的屏蔽原则：

在一个方法内，可以定义和成员变量同名的局部变量或参数，此时成员变量被屏蔽。此时如果想要访问成员变量，可以通过 this关键字来访问，this关键字来访问，this 为当前实例的引用，如果要访问类变量，可以通过类名来访问。

4.为什么double类型的数值进行运算得不到“数学上精确”的结果？

N进制可以理解为：数值×基数的幂，例如我们熟悉的十进制数123.4=1×10²+2×10+3×(10的0次幂)+4×(10的-1次幂)；其它进制的也是同理，例如二进制数11.01=1×2+1×(2的0次幂)+0+1×(2的-2次幂)=十进制的3.25。

double类型的数值占用64bit，即64个二进制数，除去最高位表示正负符号的位，在最低位上一定会与实际数据存在误差（除非实际数据恰好是2的n次方）。
举个例子来说，比如要用4bit来表示小数3.26，从高到低位依次对应2的1,0,-1,-2次幂，根据最上面的分析，应当在二进制数11.01(对应十进制的3.25)和11.10(对应十进制的3.5)之间选择。
简单来说就是我们给出的数值，在大多数情况下需要比64bit更多的位数才能准确表示出来（甚至是需要无穷多位），而double类型的数值只有64bit，后面舍去的位数一定会带来误差，无法得到“数学上精确”的结果

5.以下代码的输出结果是什么？

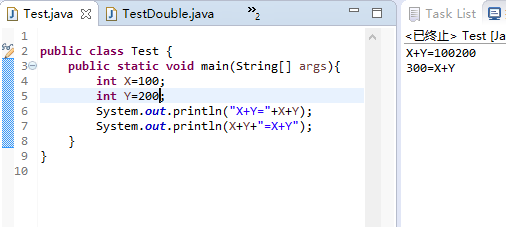
为什么会有这样的输出结果？

因为输出的是字符串，所以前一个分别输出两个字符串，而后一个表示用字符串输出两个整形的和。