我们需要接受失望,因为它是有限的;我们不会失去希望,因为它是无穷的。
一、概述
随着时间和业务的发展,数据库中表的数据量会越来越大,相应地,数据操作,增删改查的开销也会越来越大。因此,把其中一些大表进行拆分到多个数据库中的多张表中。
本篇文章是基于非事务消息的异步确保的方式来完成分库分表中的事务问题。
二、需要解决问题
2.1 原有事务
由于分库分表之后,新表在另外一个数据库中,如何保证主库和分库的事务性是必须要解决的问题。
解决办法:通过在主库中创建一个流水表,把操作数据库的逻辑映射为一条流水记录。当整个大事务执行完毕后(流水被插入到流水表),然后通过其他方式来执行这段流水,保证最终一致性。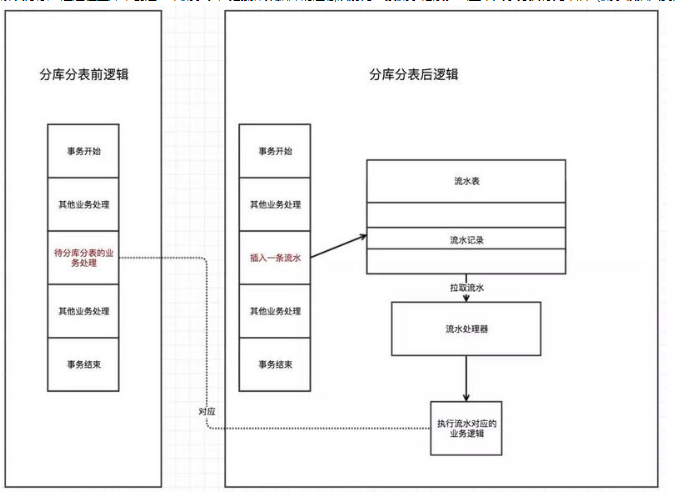
2.2 流水
所谓流水,可以理解为一条事务消息
上面通过在数据库中创建一张流水表,使用一条流水记录代表一个业务处理逻辑,因此,一个流水一定是能最终正确执行的.因此,当把一段业务代码提取流水中必须要考虑到:
- 流水延迟处理性。流水不是实时处理的,而是用过流水执行器来异步执行的。因此,如果在原有逻辑中,需要特别注意后续流程对该流水是不是有实时依赖性(例如后续业务逻辑中会使用流水结果来做一些计算等)。
- 流水处理无序性。保证即使后生成的流水先执行,也不能出现问题。
- 流水最终成功性。对每条插入的流水,该条流水一定要保证能执行成功
因此,提取流水的时候:
- 流水处理越简单越好
- 流失处理依赖越少越好
- 提取的流水在该业务逻辑中无实时性依赖
2.4 流水处理完成
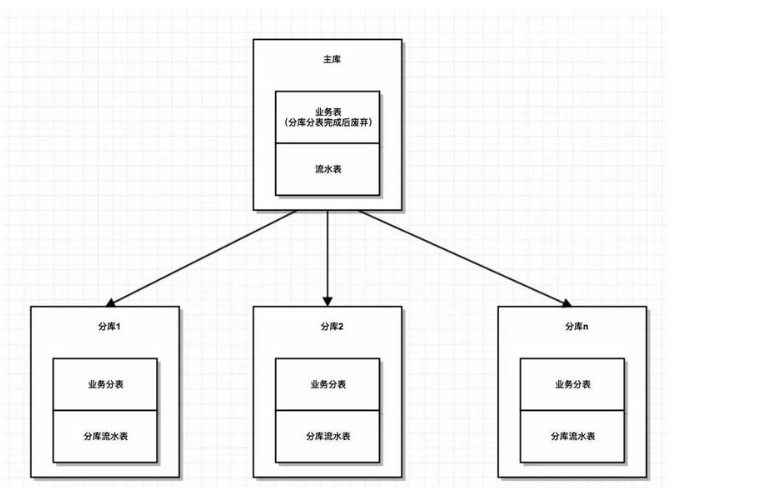
因为流水表是放在原数据库中,而流水处理完成后是操作分库,如果分库操作完成去更新老表流水消息,那么又是夸库事务,如何保证流水状态的更新和分库也是在一个事务的?
解决办法是:在分库中创建一个流水表,当流失处理完成以后,不是去更新老表状态,而是插入分库流水表中、
这样做的好处:
- 一般会对流水做唯一索引,那么如果流水重复多次执行的时候,插入分库流水表的时候肯定由于唯一索引检测不通过,整个事务就会回滚(当然也可以在处理流水事前应该再做一下幂等性判断)
- 这样通过判断主库流水是否在分库中就能判断一条流水是否执行完毕
三、流水处理器基本框架
流水处理器其实不包含任何业务相关的处理逻辑,核心功能就是:
- 通知业务接入方何时处理什么样的流水
- 检验流水执行的成功
注:流水执行器并不知道该流水表示什么逻辑,具体需要业务系统去识别后去执行相对应业务逻辑。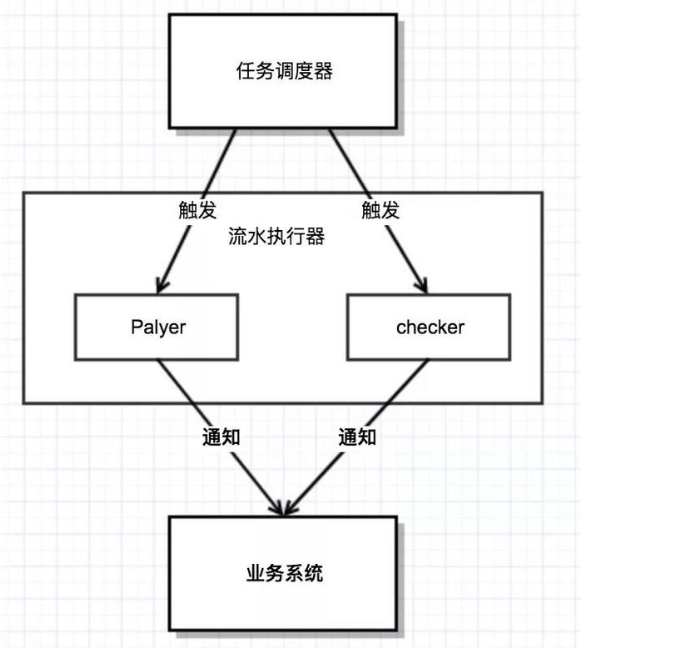
3.1 流水执行任务
流水处理调度任务就是通过扫描待处理的流水,然后通知业务系统该执行哪一条流水。
示意图如下: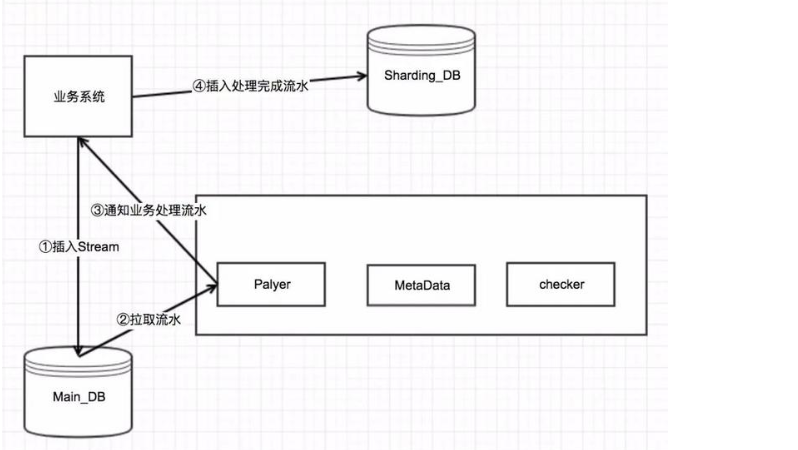
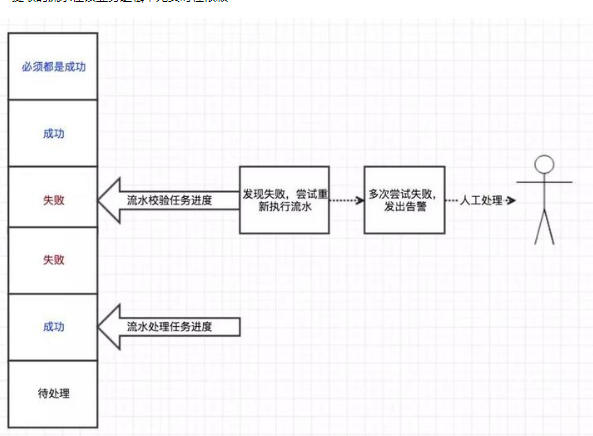
3.2 流水校验任务
流水校验任务就是要比较主库和分库中的流水记录,对执行未成功的流水通知业务系统进行重新处理,如果多次重试失败则发出告警。
流程示意图:
四、为什么不用事务消息
由于是既有项目(互联网金融,所以是绝对不容忍有任何消息丢失或者消息处理失败)进行改造,不使用事务消息有1个原因
- 需要额外引入消息队列,增加系统的复杂度,而且也需要额外的逻辑保证和消息队列通讯失败的时候处理
- 其实1不算是主要原因,而是因为事务消息需要手动的commit和rollback(使用数据库不需要),那么问题来了,spring中事务是有传递性的,那我们事务消息何时提交又是个大问题,例如 A.a()本来就是一个事务, 但是另外一个事务B.b()中又调用了A.a() 那事务消息提交是放在A.a()还是B.b()中呢?