概述
最小二乘法在某种程度上无异于机器学习中基础中的基础,且具有相当重要的地位。
optimize模块中提供了很多数值优化算法,其中,最小二乘法可以说是最经典的数值优化技术了, 通过最小化误差的平方来寻找最符合数据的曲线。在optimize模块中,使用leastsq()函数可以很快速地使用最小二乘法对数据进行拟合。
比如,有一个未知系数的二元二次函数f(x,y)=w0 x^2 + w1 y^2+w2xy+w3x+w4y+w5,这里w0~w5为未知的参数,为了确定下来这些参数,将会给定一些样本点(xi,yi,f(xi,yi)),然后通过调整这些参数,找到这样一组w0 ~ w5,使得这些所有的样本点距离函数f(x,y)的距离平方之和最小。
首先看看函数的调用格式:
scipy.optimize.leastsq(func,
x0,
args=(),
Dfun=None,
full_output=0,
col_deriv=0,
ftol=1.49012e-08,
xtol=1.49012e-08,
gtol=0.0,
maxfev=0,
epsfcn=None,
factor=100,
diag=None)
参数还是非常多的,一般来说,我们只需要前三个参数就够了他们的作用分别是:
- func:误差函数
- x0:表示函数的参数
- args()表示数据点
leastsq,它可以省去中间那些具体的求解步骤,只需要输入一系列样本点,给出待求函数的基本形状(如我刚才所说,二元二次函数就是一种形状——f(x,y)=w0 x^2 + w1y^2 + w2xy + w3x + w4y + w5,在形状给定后,我们只需要求解相应的系数w0~w6),即可得到相应的参数。至于中间到底是怎么求的,这一部分内容就像一个黑箱一样。(类似与梯度下降法)
例子
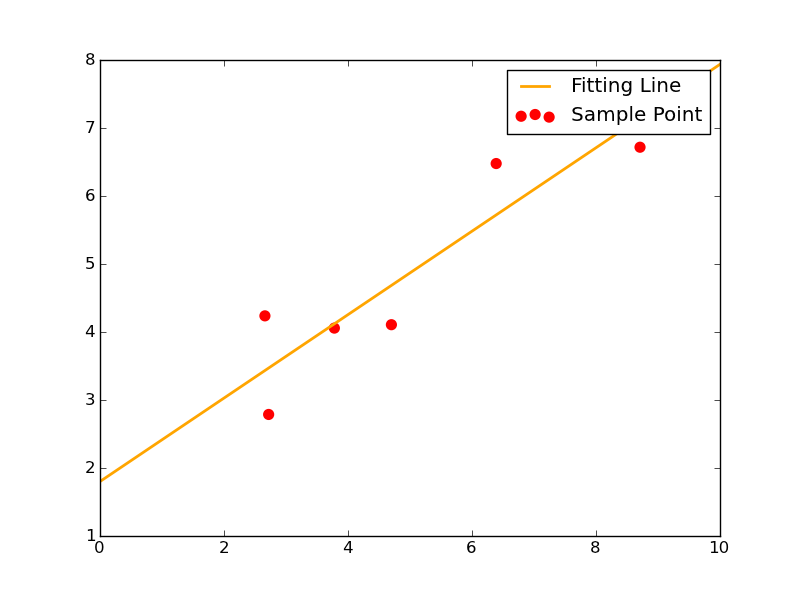
函数形为y=kx+b
Xi=np.array([8.19,2.72,6.39,8.71,4.7,2.66,3.78])
Yi=np.array([7.01,2.78,6.47,6.71,4.1,4.23,4.05])
则使用leastsq函数求解其拟合直线的代码如下:
###最小二乘法试验###
import numpy as np
from scipy.optimize import leastsq
###采样点(Xi,Yi)###
Xi=np.array([8.19,2.72,6.39,8.71,4.7,2.66,3.78])
Yi=np.array([7.01,2.78,6.47,6.71,4.1,4.23,4.05])
###需要拟合的函数func及误差error###
def func(p,x):
k,b=p
return k*x+b
def error(p,x,y,s):
print s
return func(p,x)-y #x、y都是列表,故返回值也是个列表
#TEST
p0=[100,2]
#print( error(p0,Xi,Yi) )
###主函数从此开始###
s="Test the number of iteration" #试验最小二乘法函数leastsq得调用几次error函数才能找到使得均方误差之和最小的k、b
Para=leastsq(error,p0,args=(Xi,Yi,s)) #把error函数中除了p以外的参数打包到args中
k,b=Para[0]
print"k=",k,'
',"b=",b
###绘图,看拟合效果###
import matplotlib.pyplot as plt
plt.figure(figsize=(8,6))
plt.scatter(Xi,Yi,color="red",label="Sample Point",linewidth=3) #画样本点
x=np.linspace(0,10,1000)
y=k*x+b
plt.plot(x,y,color="orange",label="Fitting Line",linewidth=2) #画拟合直线
plt.legend()
plt.show()
1、p0里放的是k、b的初始值,这个值可以随意指定。往后随着迭代次数增加,k、b将会不断变化,使得error函数的值越来越小。
2、func函数里指出了待拟合函数的函数形状。
3、error函数为误差函数,我们的目标就是不断调整k和b使得error不断减小。这里的error函数和神经网络中常说的cost函数实际上是一回事,只不过这里更简单些而已。
4、必须注意一点,传入leastsq函数的参数可以有多个,但必须把参数的初始值p0和其它参数分开放。其它参数应打包到args中。
5、leastsq的返回值是一个tuple,它里面有两个元素,第一个元素是k、b的求解结果,第二个元素我暂时也不知道是什么意思,先留下来。
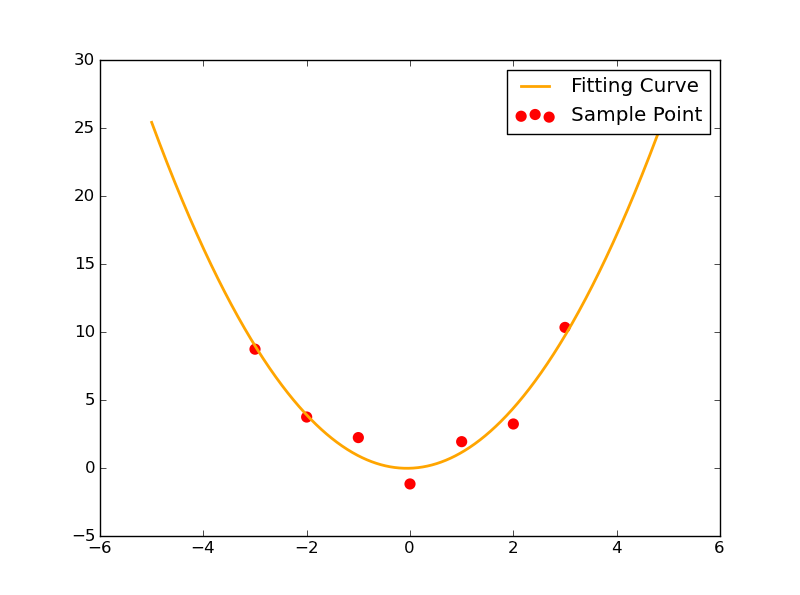
其拟合效果图如下:
函数形为y=ax^2+bx+c
这一次我们给出函数形y=ax^2+bx+c。这种情况下,待确定的参数有3个:a,b和c。
此时给出7个样本点如下:
Xi=np.array([0,1,2,3,-1,-2,-3])
Yi=np.array([-1.21,1.9,3.2,10.3,2.2,3.71,8.7])
###最小二乘法试验###
import numpy as np
from scipy.optimize import leastsq
###采样点(Xi,Yi)###
Xi=np.array([0,1,2,3,-1,-2,-3])
Yi=np.array([-1.21,1.9,3.2,10.3,2.2,3.71,8.7])
###需要拟合的函数func及误差error###
def func(p,x):
a,b,c=p
return a*x**2+b*x+c
def error(p,x,y,s):
print s
return func(p,x)-y #x、y都是列表,故返回值也是个列表
#TEST
p0=[5,2,10]
#print( error(p0,Xi,Yi) )
###主函数从此开始###
s="Test the number of iteration" #试验最小二乘法函数leastsq得调用几次error函数才能找到使得均方误差之和最小的a~c
Para=leastsq(error,p0,args=(Xi,Yi,s)) #把error函数中除了p以外的参数打包到args中
a,b,c=Para[0]
print"a=",a,'
',"b=",b,"c=",c
###绘图,看拟合效果###
import matplotlib.pyplot as plt
plt.figure(figsize=(8,6))
plt.scatter(Xi,Yi,color="red",label="Sample Point",linewidth=3) #画样本点
x=np.linspace(-5,5,1000)
y=a*x**2+b*x+c
plt.plot(x,y,color="orange",label="Fitting Curve",linewidth=2) #画拟合曲线
plt.legend()
plt.show()