前面写过一篇关于轮廓算法的文章,是把合并建筑和合并轮廓是分开对待的,并且为了使轮廓合并的时候算法简单,对x坐标使用了double类型,然后对整形的x坐标数据进行合并。这样做是为了使得需找拐点的算法容易理解,遇到拐点的时候方便辨认。但是缺点也很明显:它对所有建筑的x坐标区间(MaxX-MinX)非常敏感,区间变大的话,效率就会下降(它用double类型来遍历所有x的整形坐标,double可以使用0.5的步长)。但是如果输入的建筑横坐标数据是浮点型的话这个算法就需要再改动下才能使用,所以它的限制很多,通用性不好。原文在这里:http://www.cnblogs.com/andyzeng/p/3670432.html
有没有一个算法能解决上面提到的限制呢?
后来有时间仔细想了一下这个算法,并且重新审视了一下数据输入和数据输出的要求,发现其中的一些联系:
-----------------------
输入的建筑数据:
10 110 50
20 60 70
30 130 90
120 70 160
140 30 250
190 180 220
230 130 290
240 40 280
输出(粗体格式为轮廓高度):
10 110 30 130 90 0 120 70 160 30 190 180 220 30 230 130 290 0
-------------------------
如果单独拿出一个建筑的输入来看,10 110 50,数据代表的意思是建筑的左边边界x坐标10,建筑的高度110,建筑的右边边界50。
再看输出的格式10 110 30 130 90 0 120 70 160 30 190 180 220 30 230 130 290 0,最后一个0表示这个轮廓线的最后高度变为0,如果拿掉最后一个0,那么输出就变成10 110 30 130 90 0 120 70 160 30 190 180 220 30 230 130 290 ,这样它和单独一个建筑的数据,比如10 110 50就非常相似了,轮廓数据的意义是一个x坐标,一个高度坐标,一个x坐标,一个高度坐标....最后是一个x坐标。两个x坐标之间的高度坐标是这两个x之间的建筑高度。这样轮廓也可以看成一个封闭的建筑,它是由多个单独的建筑组成的,分解成单独的建筑就是
10 110 30,30 130 90,90 0 120,120 70 160,160 30 190,190 180 220,220 30 230,230 130 290
绿色的x坐标是我添加的,现在就明了了,两个轮廓线的合并就是可以看成两组建筑的合并,两组建筑的合并就又可以拆解成其中每两个建筑的合并。
尝试设计一个算法把合并建筑和合并轮廓统一解决。
设计一个类来表示输入建筑和输出轮廓:
其中用一个列表Data来存储建筑/轮廓的数据
索引器只是为了后面编写算法时简化一下访问,在这里不是必须的。
public class NewBuilding { public NewBuilding() { } public NewBuilding(int x1, int h, int x2) { Data.Add(x1); Data.Add(h); Data.Add(x2); } public int this[int i] { get { return Data[i]; } set { Data[i] = value; } } public List<int> Data = new List<int>(); }
//分治法合并建筑/轮廓,这个就是一个递归过程,每次都将待合并的建筑数组分成两段,然后分别递归调用合并,直到最后合并成一个建筑输出。
public static NewBuilding MergeBuildings(NewBuilding[] blds, int leftIndex, int rightIndex) { if (rightIndex == leftIndex)//one same building { return blds[leftIndex]; } else if (rightIndex - leftIndex == 1)//two buildings { return newMergeTwoBuildingsImpl(blds[leftIndex], blds[rightIndex]); } else { int middle = (rightIndex + leftIndex) / 2; NewBuilding firstOutlines = MergeBuildings3(blds, leftIndex, middle); NewBuilding secondOutlines = MergeBuildings3(blds, middle + 1, rightIndex); return newMergeTwoBuildingsImpl(firstOutlines, secondOutlines); } }
//下面为核心代码,方法 newMergeTwoBuildingsImpl是合并两个建筑/轮廓的方法,getKneePoint是寻找下一个拐点的方法
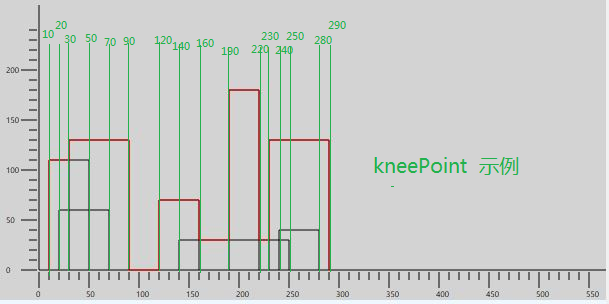
拐点定义:当轮廓高度发生变化时,在图形上就是轮廓线开始向上或者向下转向时,这个转向的x坐标点为拐点。当输出时,拐点就是把高度夹在中间的各个x轴坐标。
拐点图例:绿色标志出来的横坐标就是kneePoint,会发现所有的kneePoint横坐标都是可能产生轮廓弯曲的点的横坐标,都是需要检查的点,有些点在合并的时候被舍弃,因为它被更高的轮廓包含。如果把舍弃的点去掉,就可以尝试写出最后合并的轮廓输出了:)
接下来逐行讲解代码,row 3表示第三行代码,下同。
row1: 参数为两个建筑(可能为只包含一个建筑对象,也可能是一个复杂的多个建筑组成的轮廓建筑对象)
row 3:nb为存储合并结果的对象
row4,row5:分别定义建筑A和建筑B的游标,存储当前处理到的各自的x坐标所在的索引值,如下图所示。
row6:分别定义两个建筑的和坐标和纵坐标,分别记录当前待合并的两个简单建筑(从轮廓线里面取出来的,后面讲到取法)
row7:定义两个长度变量,简化后面的代码
row8:取得两个复杂建筑的x起点,在坐标上表现为取得最左边建筑轮廓线的边界x坐标
row9:只要至少一个轮廓建筑没有处理完就继续处理
row12-row16:当两个轮廓都处理到最后一个点时,把最后的最大的x坐标添加到nb里面,退出while循环,全部处理完了
row18-row21:对A轮廓处理到了最右边的边界点时,总是取A[lenthA - 1],0,0为待合并简单建筑,其实就是放弃了合并,等待B把剩下的轮廓加进来
row22-row25:对A正常取得待合并的简单建筑数据
row26-row33:同row18-row25
row35:取得当前拐点的高度数值
row36-row41:当为第一个加入结果的x边界和高度值时,或者与前面已经合并的轮廓线不等高时才加入新合并的结果
row43:关键,取得下一个拐点,即下一个x坐标值,这个值为两个正在合并的简单建筑的所有x坐标中第一个大于当前拐点的值,也可以理解为下一个可能出现轮廓线上下变向的x坐标。
row45,row46:判断新的拐点是否已经超出各自的轮廓线,并且如果轮廓线还没处理完,那么把游标指向下一个x边界。
row50-row61:解决row43的问题,取得第一个大于当前拐点的值
1 private static NewBuilding newMergeTwoBuildingsImpl(NewBuilding A, NewBuilding B) 2 { 3 NewBuilding nb = new NewBuilding(); 4 int cursorA = 0;//the cursor for the first build 5 int cursorB = 0;////the cursor for the second build 6 int ax1, ah, ax2, bx1, bh, bx2; 7 int lenthA = A.Data.Count, lenthB = B.Data.Count;//长度都必为奇数,迭代步长为2,最后一个点为迭代终止点 8 int kneePointX = Math.Min(A[cursorA], B[cursorB]);//拐点 9 while (cursorA < lenthA || cursorB < lenthB) 10 { 11 //边界情况 12 if (cursorA == lenthA - 1 && cursorB == lenthB - 1) 13 { 14 nb.Data.Add(Math.Max(A[cursorA], B[cursorB])); 15 break; 16 } 17 18 if (cursorA >= lenthA - 1) 19 { 20 ax1 = A[lenthA - 1]; ah = 0; ax2 = ax1; 21 } 22 else 23 { 24 ax1 = A[cursorA]; ah = A[cursorA + 1]; ax2 = A[cursorA + 2]; 25 } 26 if (cursorB >= lenthB - 1) 27 { 28 bx1 = B[lenthB - 1]; bh = 0; bx2 = bx1; 29 } 30 else 31 { 32 bx1 = B[cursorB]; bh = B[cursorB + 1]; bx2 = B[cursorB + 2]; 33 } 34 //高度取当前x<=kneePointX<=x2的建筑高度的最大值 35 int h = (Math.Max(ax1 <= kneePointX && kneePointX <= ax2 ? ah : 0, bx1 <= kneePointX && kneePointX <= bx2 ? bh : 0)); 36 if ((nb.Data.Count == 0) || (nb.Data.Count > 0 && nb.Data.Last() != h))//第一个点或者与前面的轮廓不等高点才添加新的轮廓 37 { 38 //x点取kneePointX,封闭前面的轮廓,加入新的高度 39 nb.Data.Add(kneePointX); 40 nb.Data.Add(h); 41 } 42 //关键,下一个拐点的取法:取大于kneePointX的最小点 43 kneePointX = getKneePoint(new int[] { ax1, ax2, bx1, bx2 }, kneePointX); 44 //关键:检查两个轮廓的游标是否需要向前步进 45 if (ax2 <= kneePointX && cursorA < lenthA - 1) cursorA = cursorA + 2; 46 if (bx2 <= kneePointX && cursorB < lenthB - 1) cursorB = cursorB + 2; 47 } 48 return nb; 49 } 50 private static int getKneePoint(int[] arr, int kneePointX) 51 { 52 int minMax = int.MaxValue; 53 for (int i = 0; i < arr.Length; i++) 54 { 55 if (arr[i] > kneePointX && arr[i] < minMax) 56 { 57 minMax = arr[i]; 58 } 59 } 60 return minMax; 61 }
调用方法MergeBuildings并取得结果后,在所得结果上面再添加一个0,就是题目所要求的输出了。
此算法要比之前的算法快几十倍,10万个随机建筑合并需要大约80ms(不同机器上可能略有不同)。
算法复杂度分析:
每次将n个建筑平均分成两组建筑,每组数量为n/2,合并两个简单建筑(长方体型的简单建筑)的时候,检查一次kneePoint大约需要20次比较,大约12次数据赋值操作。最少2个kneePoint,最多7个kneePoint
最好情况,每次两个kneePoint,总的比较和数据移动次数为 32*2,即T(2)=T(1)=32*2=64,P(n)表示n个建筑合并,P(n)的时间最好是64n
T(n)=2T(n/2)+P(n)=2[2T[n/4]+P(n/2)]+P(n)=2[2T[n/4]+((64n)/2)n]+(64n)=2[2T[n/4]]+(64n)+(64n)=(64n)+(64n)+.(logn个)..+(64n)=64n*Logn
所以此时时间复杂度O(nLogn)
最坏情况,每个建筑都不相交或者每两个建筑相交(建筑相包含但高度高的范围被包含在高度低的里面)都产生3个高度。此时P(n)的时间是32*7n
T(n)=2T(n/2)+P(n)=32*7*n*Logn
所以此时时间复杂度O(nLogn)
所以此算法的平均时间复杂度为O(nLogn)
代码下载
作者:Andy Zeng
欢迎任何形式的转载,但请务必注明出处。