设:校验位的个数为r,能表示2^r个信息,1个表示“没错误”, 2^r -1个指出错误发生在哪一位.
k= 2^r –1-r个信息可用于纠正数据位.
2^r≥k+r+1
若要检测并纠正一位错,同时发现两位错,r,k应满足下列关系: 2^r-1≥k+r (见表3.8)
校验位排列在 2^(i–1) (i =0,1,2,…)的位置上
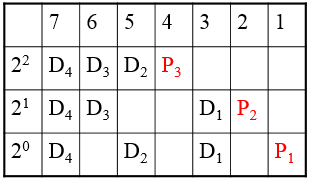
例:有一个编码 为D4D3D2D1,由此生成一个海明码
7 6 5 4 3 2 1
D4 D3 D2 P3 D1 P2 P1
2^2 2^1 2^0
有一字节的信息需生成海明码
D8 D7 D6 D5 P4 D4 D3 D2 P3 D1 P2 P1
8 4 2 1
P3= D4⊕D3 ⊕D2
0 = 1 ⊕ 0 ⊕ 1
P2= D4 ⊕D3 ⊕D1
0 = 1 ⊕ 0 ⊕ 1
P1 = D4 ⊕D2 ⊕D1
1 = 1 ⊕ 1 ⊕ 1
最后 海明码为1010101
7=4+2+1 6=4+2 5=4+1 3=2+1
设 海明校验码共m位(m=K+r),形如:
海明码编码规律通常是:
1.校验位与数据位之和为m,每个校验位Pi在被分在位号2^(i-1)的位置,其余数据位由低到高排列.
2.海明码的每一位Hi由多个校验位校验,关系是:被校验的每一位的位号等于校验它的各校验位位号之和.
按上述规律讨论一个字节的海明码.
D8D7D6D5 D4D3D2D1
8位二进制数,k=8,根据2^r-1≥k+r , r应为5,m=13
1.校验位与数据位之和为m,每个校验位Pi被分在位号2^(i-1)的位置, P5~P1对应H13,H8,H4, H2 H1
其余为数据位,形如:
H13 H12 H11 H10 H9 H8 H7 H6 H5 H4 H3 H2 H1
P5 D8 D7 D6 D5 P4 D4 D3 D2 P3 D1 P2 P1
13 4 1 2 1 8 1 2 1 4 1 2 1
8 2,8 8 8 2,4 4 4 2
每一位的位号等于校验它的各校验位位号之和.
P1参与了D1 D2 D4 D5 D7的校验
P2参与了D1 D3 D4 D6 D7的校验
P3参与了D 2 D3 D4 D8的校验
由此,可以找出有关数据位形成Pi值偶校验的结果。
P1=D1⊕ D 2 ⊕ D4 ⊕ D5 ⊕ D7
P2 =D1 ⊕ D3 ⊕ D4 ⊕ D6 ⊕ D7
P3 =D 2 ⊕ D3 ⊕ D4 ⊕ D8
P4 =D 5 ⊕ D6 ⊕ D7 ⊕ D8
如果要分清是两位出错还是一位出错,还要补充一个P5总校验位。使:
P5=D1⊕D2⊕D3⊕D4⊕D5⊕D6⊕D7⊕D8⊕P4⊕P3
⊕P2⊕P1
由此,可以得出偶校验组。
S1= P1⊕ D1⊕ D 2 ⊕ D4 ⊕ D5 ⊕ D7
S2= P2⊕D1 ⊕ D3 ⊕ D4 ⊕ D6 ⊕ D7
S3= P3⊕ D 2 ⊕ D3 ⊕ D4 ⊕ D8
S4= P4⊕ D 5 ⊕ D6 ⊕ D7 ⊕ D8
S5= P5⊕P4⊕P3⊕P2⊕ P1⊕D1⊕D2⊕D3⊕D4⊕D5⊕D6⊕D7⊕D8
S1 ~ S5能反映出13位海明码的出错情况.
S1= P1⊕ D1⊕ D 2 ⊕ D4 ⊕ D5 ⊕ D7
S2= P2⊕D1 ⊕ D3 ⊕ D4 ⊕ D6 ⊕ D7
S3= P3⊕ D 2 ⊕ D3 ⊕ D4 ⊕ D8
S4= P4⊕ D 5 ⊕ D6 ⊕ D7 ⊕ D8
S4 ~ S1为全0,说明没错. S4 ~ S1不为全0,说明有错. S5=1说明1位出错,而S5=0说明2位错,不再有效,且不能查出是哪2位出错。
S4 ~ S1的编码值正好等于出错的海明码的位号.如:1100和1011,分别表示H12(D8)和H11(D7)出错。
如果 S4 ~ S1中仅有一个不为0,则表示校验位出错. S1≠0时P1(即H1)出错; S2≠0时P2(即H2)出错; S3≠0时P3(即H4)出错; S4≠0时P4(即H8)出错.
如果S4 ~ S1中有2个或2个以上不为0,则表示有1位数据出错(两位[指r=4时]或者两位以上数据同时出错则检查不出来)。 S4 ~ S1的编码值正好等于出错的海明码的位号.如:1100和1011,分别表示H12(D8)和H11(D7)出错。
假设S1 、 S4不为0, S2 、 S3为0,则说明P1和P4两个校验位出错,查公式,在S1和S4中同时出现而在S2和S3中不出现的数据仅有D5一个,故D5出错。或者查表, P1对应H1 , P4对应H8 ,出错的海明码位号=1+8=9,即H9出错, H9对应D5 。