
import numpy as np
# Write a function that takes as input a list of numbers, and returns
# the list of values given by the softmax function.
def softmax(L):
pass
expL = np.exp(L)
sumExpL = sum(expL)
result = []
for i in expL:
result.append(i*1.0/sumExpL)
return result
python编写交叉熵公式:
import numpy as np
def cross_entropy(Y, P):
Y = np.float_(Y)
P = np.float_(P)
return -np.sum(Y * np.log(P) + (1 - Y) * np.log(1 - P))
import numpy as np
def cross_entropy(Y, P):
Y = np.float_(Y)
P = np.float_(P)
return -np.sum(Y * np.log(P) + (1 - Y) * np.log(1 - P))
MSE:
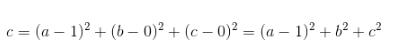
cross-entropy:
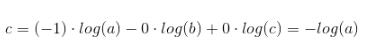
从上述的公式可以看出,交叉熵的损失函数只和分类正确的预测结果有关系,而MSE的损失函数还和错误的分类有关系,该分类函数除了让正确的分类尽量变大,还会让错误的分类变得平均,但实际在分类问题中这个调整是没有必要的。
但是对于回归问题来说,这样的考虑就显得很重要了。所以,回归问题熵使用交叉上并不合适。
以上这篇python编写softmax函数、交叉熵函数实例就是小编分享给大家的全部内容了,希望能给大家一个参考,也希望大家多多支持。