1、快速傅里叶变换的实现
什么是傅里叶定理?
法国科学家傅里叶提出,任何一条周期性曲线,无论多么跳跃或不规则,都能表示成一组光滑正弦曲线叠加之和。
什么是傅里叶变换?
傅里叶变换即是把一条周期性曲线拆解成一组光滑正弦曲线的过程。
傅里叶变换的目的是可将时域(即时间域)上的信号转变为频域(即频率域)上的信号,随着域的不同, 对同一个事物的认知角度也随之改变,因此在时域中某些不好处理的地方,在频域就可以较为简单地处理。这就可以大量减少处理信号存储量。
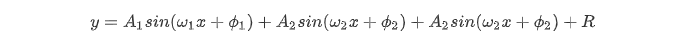
所以傅里叶变换可以把一个比较复杂的函数转换为多个简单函数的叠加,看问题的角度也从时间域转到了频率域,有些问题处理起来就会比较简单。
傅里叶变换相关函数
导入快速傅里叶变换所需模块
import numpy.fft as nf
通过采样数域采样周期求得傅里叶变换分解所得曲线的频率序列
freqs = nf.fftfreq(采样熟练,采样周期)
通过原函数值得序列经过快速傅里叶变换得到一个复数数组,复数的模代表的是振幅,复数的辐角代表初相位
nf.fft(原函数序列值) -> 目标函数序列值(复数数组)
通过一个复数数组(复数的模代表振幅,复数的辐角代表初相位)经过逆傅里叶变换得到合成的函数值数组
nf.ifft(目标函数值序列(复数)) -> 原函数值序列
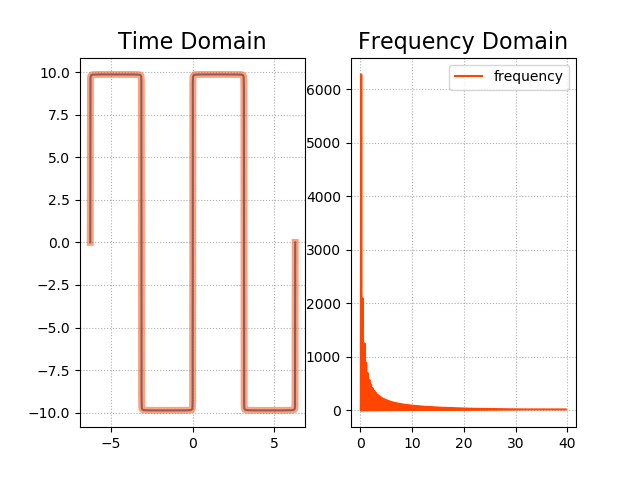
案例:
import numpy as np
import matplotlib.pyplot as plt
import numpy.fft as nf
x = np.linspace(-2 * np.pi, 2 * np.pi, 1000)
y = np.zeros(x.size)
for i in range(1, 1000):
y += 4 * np.pi / (2 * i - 1) * np.sin((2 * i - 1) * x)
plt.figure('FFT', facecolor='lightgray')
plt.subplot(121)
plt.title('Time Domain', fontsize=16)
plt.grid(linestyle=':')
plt.plot(x, y, label=r'$y$')
# 针对方波y做fft
comp_arr = nf.fft(y)
y2 = nf.ifft(comp_arr).real
plt.plot(x, y2, color='orangered', linewidth=5, alpha=0.5, label=r'$y$')
# 绘制频域图形
plt.subplot(122)
freqs = nf.fftfreq(y.size, x[1] - x[0])
pows = np.abs(comp_arr) # 复数的模
plt.title('Frequency Domain', fontsize=16)
plt.grid(linestyle=':')
plt.plot(freqs[freqs > 0], pows[freqs > 0], color='orangered', label='frequency')
plt.legend()
plt.savefig('fft.png')
plt.show()
运行结果:
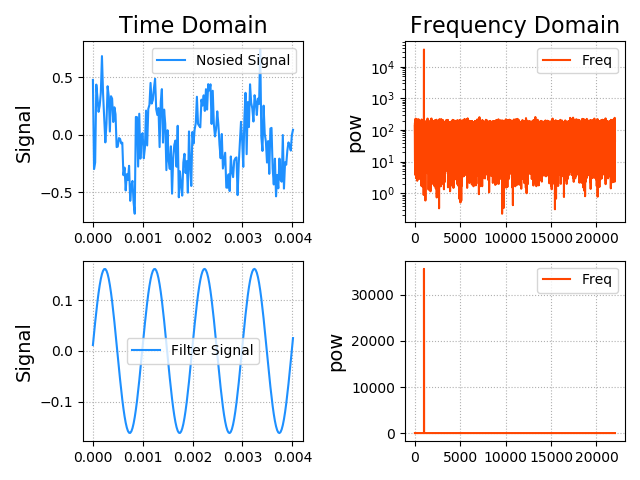
2、基于傅里叶变换的频域滤波
import numpy as np
import numpy.fft as nf
import matplotlib.pyplot as plt
import scipy.io.wavfile as sw
# 获取采样率、采样位移
sample_rate, sigs = sw.read('noised.wav')
print(sample_rate, sigs.shape)
sigs = sigs / (2 ** 15)
times = np.arange(sigs.size) / sample_rate
# 绘图
plt.figure('Filter', facecolor='lightgray')
plt.subplot(221)
plt.title('Time Domain', fontsize=16)
plt.ylabel('Signal', fontsize=14)
plt.grid(linestyle=':')
plt.plot(times[:178], sigs[:178], color='dodgerblue', label='Nosied Signal')
plt.legend()
# fft变换后绘制频域图
comp_arr = nf.fft(sigs)
pows = np.abs(comp_arr)
freqs = nf.fftfreq(sigs.size, times[1] - times[0])
plt.subplot(222)
plt.title('Frequency Domain', fontsize=16)
plt.ylabel('pow', fontsize=14)
plt.grid(linestyle=':')
plt.semilogy(freqs[freqs > 0], pows[freqs > 0], color='orangered', label='Freq')
plt.legend()
# 在频谱中去除噪声
maxpow_freq = freqs[pows.argmax()]
noised_inds = np.where(freqs != maxpow_freq)
# 噪声的复数全改为0
comp_arr[noised_inds] = 0
# 绘制降噪之后的频谱图形
pows = np.abs(comp_arr)
plt.subplot(224)
plt.ylabel('pow', fontsize=14)
plt.grid(linestyle=':')
plt.plot(freqs[freqs > 0], pows[freqs > 0], color='orangered', label='Freq')
plt.legend()
# 逆向傅里叶变换,输出时域函数图形
filter_sigs = nf.ifft(comp_arr).real
plt.subplot(223)
plt.ylabel('Signal', fontsize=14)
plt.grid(linestyle=':')
plt.plot(times[:178], filter_sigs[:178], color='dodgerblue', label='Filter Signal')
plt.legend()
# 保存滤波后的信号
sw.write('filter.wav', sample_rate, (filter_sigs * 2 ** 15).astype(np.int16))
plt.tight_layout()
plt.savefig('filter.png')
plt.show()
运行结果: