常见排序算法基于JS的实现

一：冒泡排序

1. 原理

a. 从头开始比较相邻的两个待排序元素，如果前面元素大于后面元素，就将二个元素位置互换

b. 这样对序列的第0个元素到n-1个元素进行一次遍历后，最大的一个元素就“沉”到序列的最后位置（第n-1个位置，n为待排序元素个数）

c．排除此次排序最后面的那个元素(n=n-1)，继续对剩余序列重复前面两步

d. 当(n= n-1)=0时，排序完成

2. 具体实现

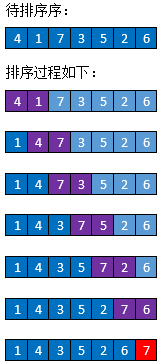
以如下待排序序列为例：

到此，第一次冒泡完成，最大值7冒泡到最后面。

然后继续对除最后元素（7）外的序列进行冒泡排序。具体实现如下：

/**
 * 冒泡排序
 * @param {Array} arr - 整型数组
 * @returns {Array} ret - 排好序的数组
 */

function bubbleSort(arr) {
    var n = arr.length,
        i = 0,
        temp;

    while(--n) {

        while (i < n) {

            // 如果前一个数大于后一个数，则互换位置
            if(arr[i] > arr[i+1]) {
                temp = arr[i];
                arr[i] = arr[i+1];
                arr[i+1] = temp;
            }

            i++;
        }

        // 每次冒泡完成后，将i复位
        i = 0;
    }

    return arr;
}

// 基于qunit的测试
test('bubble-sort', function () {
    var arr1 = [6,2,4,3];
    var arr2 = [28,13,4,19,10];
    var arr3 = [2,3,2,4,2,5];

    propEqual(bubbleSort(arr1), [2,3,4,6]);
    propEqual(bubbleSort(arr2), [4,10,13,19,28]);
    propEqual(bubbleSort(arr3), [2,2,2,3,4,5]);
});

二：选择排序

1. 原理

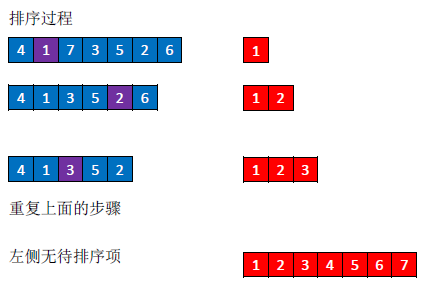
a. 首先在待排序序列中找到最小元素，放入储存有序序列中。同时从待排序序列中删除这个元素

b. 继续从未排序序列中找到最小元素，然后a步中的有序列序列中

c. 以此类推，直到待排序序列元素个数为0

2.  具体实现：

/**
 * 选择排序
 * @param {Array} arr
 * @returns {Array} ret
 */
function selectionSort(arr) {
    var ret = [],
        min,
        i;

    while(arr.length) {

        // TODO 应该自己实现一个求数组中的最小值方法
        min  = Math.min.apply(null, arr);

        ret.push(min);

        // 从待排序数组中删除这个元素
        arr.splice(arr.indexOf(min), 1);

    }

    return ret;
}

// qunit
test('selection-sort', function () {
    var arr1 = [1,5,3,6,4,2];
    var arr2 = [1,5,4,6,4,2];

    propEqual(selectionSort(arr1), [1,2,3,4,5,6]);
    propEqual(selectionSort(arr2), [1,2,4,4,5,6]);

});

三： 插入排序

1. 排序原理：

a. 从待排序序列第0个元素开始排序，该元素可以认为已经是有序的

b. 取出下一个元素，在已经排序的元素序列中从后向左遍历

c. 如果已排序元素大于新元素，将该元素移到下一位置

d. 重复步骤c，直到找到一个已排序的元素，此元素不大于新元素；或者元素位于有有序序列开始位置

e. 将新元素插入到此元素后面

f. 重复步骤b~e,直接待排元素个数为0

2. 具体实现

 

/**
 * 插入排序
 * @param {Array} arr
 * @returns {Array} ret
 */
function insertionSort(arr) {

    // 从1开始，因为一个元素的序列，始终是有序的
    for(var i = 1, j; i < arr.length; i++) {

        j = i;

        // 保存待排序元素
        v= arr[j];

        // 如果有序序列中的元素大于待插入的元素，则有序列序列中的元素向后移动一个位置
        // 向后移到一个位置，会覆盖待排序的元素，但我们前面有保存待排序元素，所以待排序元素不会丢失
        // 同时，也留出一个位置，以插入待排序元素
        // 直到找一个已经排序的元素，其不大于待排序元素，将待排序元素插入到这里。
        // 如果遍历到有序序列的开始位置，也不存在一个元素不大于待排序元素，则将待排序元素插入到已经排序序列的开始

        while(arr[j-1] > v) {
            arr[j] = arr[j-1];
            j--;

            if(j === 0) {
                break;
            }
        }

        arr[j] = v;
    }

    return arr;
}

// qunit
test('insertion-sort', function () {
    var arr1 = [1,5,3,6,4,2];
    var arr2 = [1,5,4,6,4,2];

    propEqual(insertionSort(arr1), [1,2,3,4,5,6]);
    propEqual(insertionSort(arr2), [1,2,4,4,5,6]);

});

四：希尔排序

1.  排序原理：

a. 设定一个间距d，将待排序序列分组

b. 对分组使用插入排序

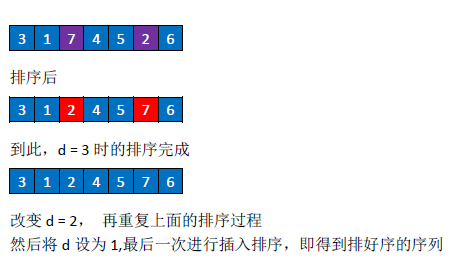
c. 改变d, 再次分组

d. 再次对上面的分组使用插入排序

e. 重复上面的步骤，直至d为1，并进行最后一次插入排序，得到排好序的序列

2. 具体实现

希尔排序过程中，涉及到选择一组间距序列，这个序列叫叫希尔增量。希尔增量的奥妙以后有时间再研究。

/**
 * 希尔排序
 * @param {Array} arr
 * @returns {Array}
 */
function shellSort(arr) {

    // 动态取得一个希尔增量

    var N = arr.length;
    var h = 1;

    var i, j, v;

    // 产生希尔增量序列第一个值
    while (h < N / 3) {
        h = 3 * h + 1; // ①
    }

    // 对分组使用插入排序，同时改变希尔增量值，直到其为1，并进行最后一次插入排序，得到有序序列
    // 第一次插入排序，都是可以将待排序序列排成有序序列的
    // 不停运用插入排序，其实是减少了元素在排序过程中移动的次数
    while (h >= 1) {
        for (i = 1; i < arr.length; i++) {

            j = i;
            v = arr[j];

            while (j > 0 && arr[j - 1] > v) {
                arr[j] = arr[j - 1];
                j--;
            }

            arr[j] = v;
        }

        h = (h - 1) / 3; // 从①可以保证，肯定能除尽的
    }

    return arr;
}

// qunit
test('shell-sort', function () {
    var arr1 = [1,5,3,6,4,2,22,34,11,12,45];
    var arr2 = [1,5,4,6,4,2];

    propEqual(shellSort(arr1), [1,2,3,4,5,6,11,12,22,34,45]);
    propEqual(shellSort(arr2), [1,2,4,4,5,6]);

});

五. 归并排序

1. 排序原理：

归并排序主要分两步：

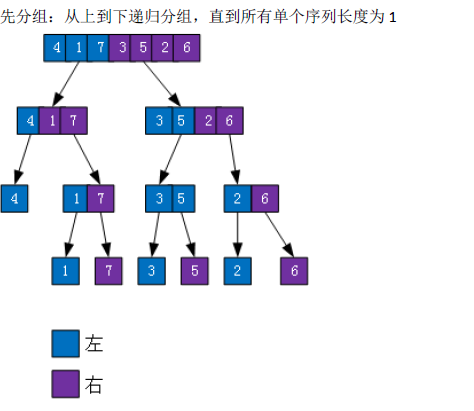
a. 分组

对待排序序列按二分法分成两个小序列，并一直递归下去，直到序列长度为1（长度为1 的序列是有序的）

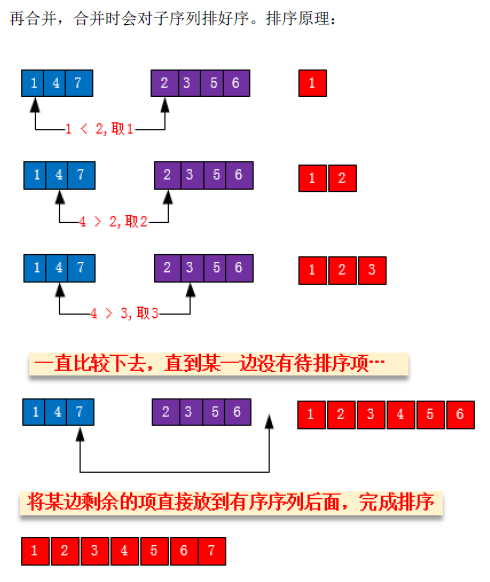
b. 合并

将排好序的数组合并成有序数列，最后得到排序结果

2. 具体实现

// 归并排序
function mergetSort(arr) {

    if(arr.length === 1) {
        return arr;
    }

    var leftArr = arr.slice(0, Math.floor(arr.length / 2));
    var rightArr = arr.slice(leftArr.length);

    // 递归
    return merge(mergetSort(leftArr), mergetSort(rightArr));

    // 合并有序序列
    function merge(arrLeft, arrRight) {

        var indexLeft = 0,
            indexRight = 0,
            sl = arrLeft.length,
            sr = arrRight.length,
            ret = [];


        while(true) {
            if(indexLeft < sl && indexRight < sr) {
                if(arrLeft[indexLeft] < arrRight[indexRight]) {
                    ret.push(arrLeft[indexLeft]);
                    indexLeft++;
                } else {
                    ret.push(arrRight[indexRight]);
                    indexRight++;
                }
            } else {
                if(indexLeft < indexRight) {
                    ret = ret.concat(arrLeft.slice(indexLeft));
                } else {
                    ret = ret.concat(arrRight.slice(indexRight));
                }
                break;
            }
        }

        return ret;
    }

}

// qunit
test('merge-sort', function () {
    var arr1 = [28,13,4,19,10];
    var arr2 = [1,5,4,6,4,2];

    propEqual(mergetSort(arr1), [4,10,13,19,28]);
    propEqual(mergetSort(arr2), [1,2,4,4,5,6]);
});

六： 快速排序

1. 排序原理

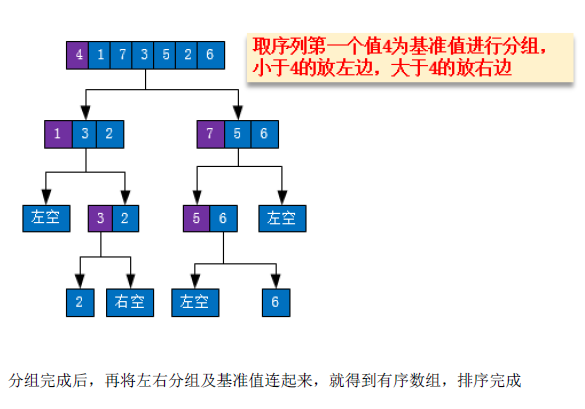
a. 从序列中挑出一个元素，称为 "基准"（pivot），

b. 重新排序序列，所有元素比基准值小的元素摆放在基准前面，所有元素比基准值大的摆在基准后面

c. 把新得到的序列再通过上面的方法排序。当序列长度为1或0时结束递归

2. 具体实现

// 快速排序
function quickSort(arr) {
    var pivot = arr[0];
    var i = 1;
    var leftArr= [],
        rightArr = [];

    if(arr.length === 0) {
        return [];
    }

    if(arr.length === 1) {
        return arr;
    }

    for(; i < arr.length; i++) {
        if(arr[i] < pivot) {
            leftArr.push(arr[i]);
        } else {
            rightArr.push(arr[i]);
        }
    }

    return quickSort(leftArr).concat(pivot, quickSort(rightArr));
}

// qunit
test('quick-sort', function () {
    var arr1 = [6,2,4,3];
    var arr2 = [28,13,4,19,10];
    var arr3 = [4,1,7,3,5,2,6];

    propEqual((quickSort(arr1)), [2,3,4,6]);
    propEqual(quickSort(arr2), [4,10,13,19,28]);
    propEqual(quickSort(arr3), [1,2,3,4,5,6,7]);
});

小结：

本文把常见的排序算法（冒泡，选择，插入，希尔，归并，快速排序）基于JS实现了一遍，练习一下算法，还是有助于提高编程思维的。比如求一个数组的最大值。我们知道可以这样：

var max = Math.min.applu(null, arr)

但是浏览器内部是怎么实现的呢，又或者假设浏览器没提供这个方法，我们自己怎么做呢？其实通过一次向左冒泡就可以得到最小值：

function getMinValue(arr) {
    var i = arr.length, j;

    j = i;

    while(--j) {
        if(arr[j - 1] > arr[j]) {
            arr[j - 1] = [arr[j - 1], arr[j]];
            arr[j] = arr[j - 1][0];
            arr[j- 1] = arr[j - 1][1];
        }
    }

    // 返回最小值
    return arr[0];
}