【LOJ】#2066. 「SDOI2016」墙上的句子

题解

我一直也不会网络流……orz

我们分析下这道题，显然和行列没啥关系，就是想给你n + m个串

那么我们对于非回文单词之外的单词，找到两两匹配的反转单词（即使另一个反转单词不会出现也要建出来）

具体就是我们建一个hash表，遇见一个单词读进来，把这个单词反转之后再存进哈希表里

然后我们把一对反转单词挑出来，按照字典序，字典序小的往字典序大的连一条流量为2的边

那么现在我们考虑一下加入阅读方式都已经被全部确定，那么网络流的建图方式就应该是
如果顺着给定的顺序是字典序较小的，那么就向给定循序读的单词连一条正无穷的边
如果顺着给定顺序是字典序较大的，那么给定顺序读出的单词就向这一行或一列连一条正无穷的边

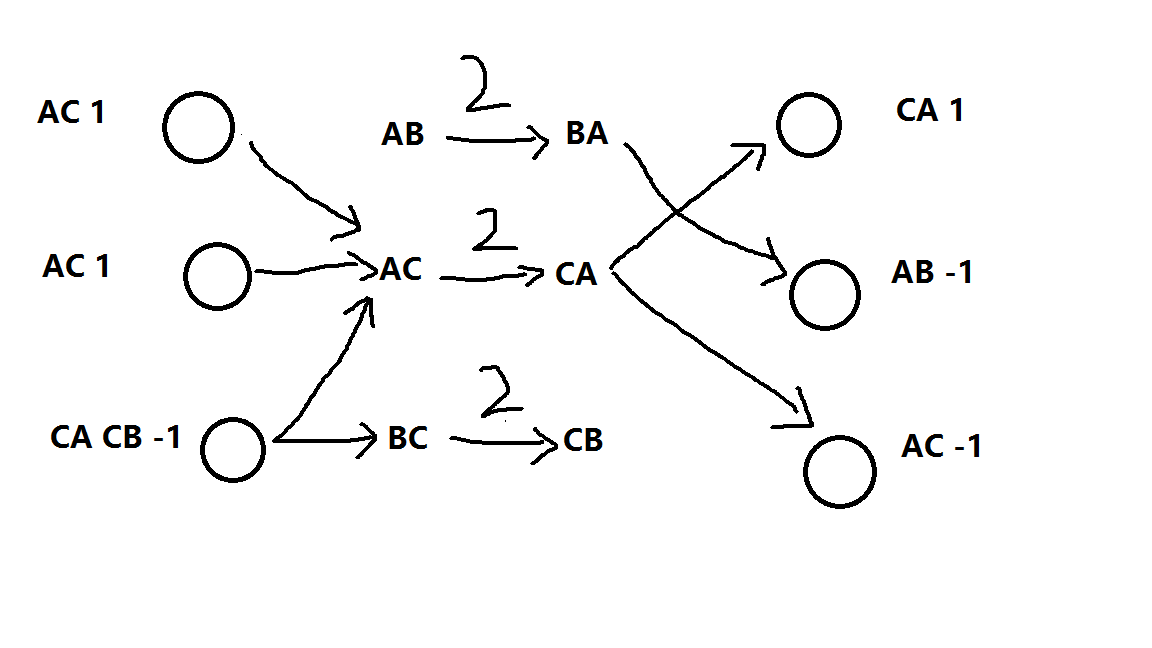
跑最大流就是答案

现在我们有了未知顺序的边，那么我们就要求了某些单词（这里正反单词算一种）必须全是以字典序较小的方式读，或者全是以字典序较大的方式读

这个限制可以用最大流等于最小割，可以想一下
如果我们需要反转部分在某些串里字典序较小的单词，从而使整个0串全是字典序较大的单词，那么这些串所连的单词所在的边就会满流
同理，如果反转字典序较大的单词，靠近汇点的一边单词会满流
因为最大流等于最小割，所以总会选择较小的一边流满

所以我们的连边方式就是0串所有单词的字典序较大的一边向0串连正无穷边，0串向所有单词字典序较小的一边连正无穷的边

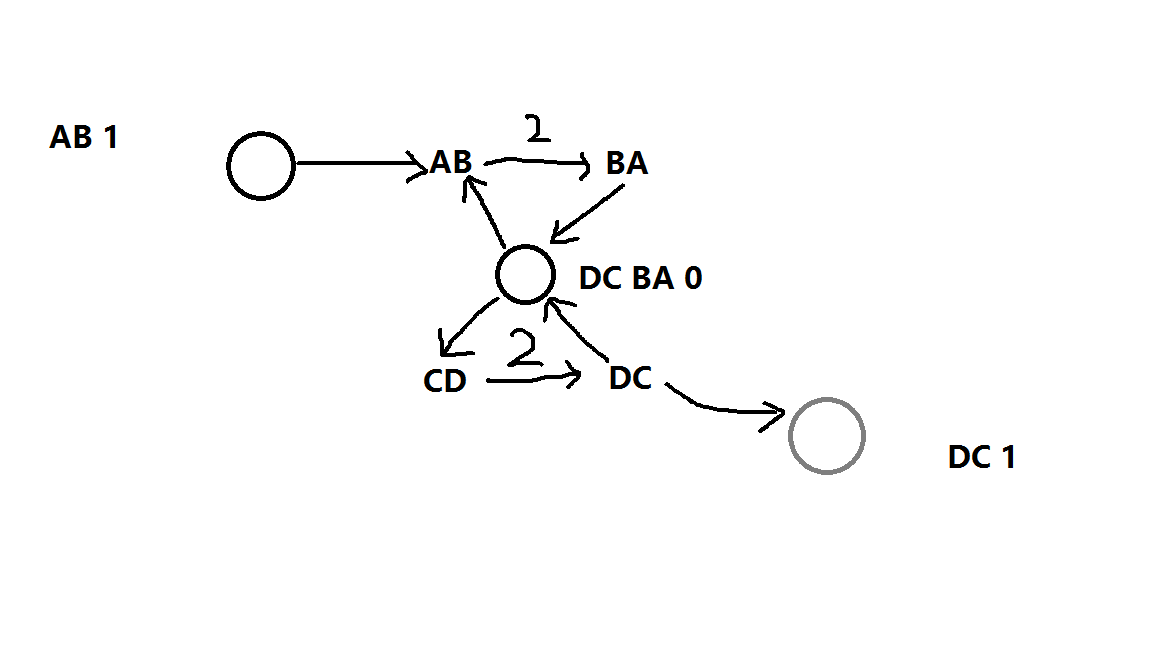
跑一遍最大流加上回文单词个数就是答案了

我的代码怎么又将近写了8K= =

代码

#include <bits/stdc++.h>
#define enter putchar('
')
#define space putchar(' ')
#define pii pair<int,int>
#define fi first
#define se second
#define mp make_pair
#define MAXN 1000005
#define mo 999999137
#define pb push_back
//#define ivorysi
using namespace std;
typedef long long int64;
typedef double db;
template<class T>
void read(T &res) {
    res = 0;T f = 1;char c = getchar();
    while(c < '0' || c > '9') {
        if(c == '-') f = -1;
        c = getchar();
    }
    while(c >= '0' && c <= '9') {
        res = res * 10 + c - '0';
        c = getchar();
    }
    res *= f;
}
template<class T>
void out(T x) {
    if(x < 0) {x = -x;putchar('-');}
    if(x >= 10) out(x / 10);
    putchar('0' + x % 10);
}
int N,M;
char s[105][105];
int H[105],L[105];
int e[105];
struct Word{
    char s[75];
    int hsh;
    friend bool operator < (const Word &a,const Word &b) {
        return a.hsh < b.hsh;
    }
    friend bool operator == (const Word &a,const Word &b) {
        return a.hsh == b.hsh;
    }
}C[10005];
int op[10005],revcnt;
bool rev[10005],isSmall[10005];
struct node {
    int to,next,cap;
}E[100005];
int sumE,head[10005],cnt,S,T;
int last[10005],dis[10005],gap[10005];
map<int,int> hash_list;
vector<int> W;
void add(int u,int v,int c) {
    E[++sumE].to = v;
    E[sumE].next = head[u];
    E[sumE].cap = c;
    head[u] = sumE;
}
void addtwo(int u,int v,int c) {
    add(u,v,c);add(v,u,0);
}
int calc(char *s,int len) {
    int res = 0;
    for(int i = 1 ; i <= len ; ++i) {
        res = (res + 1LL * e[i - 1] * (s[i] - 'A' + 1) % mo) % mo;
    }
    return res;
}
void Insert(int id,char *t,int len) {
    t[len + 1] = '';
    memcpy(C[id].s,t,sizeof(char) * (len + 2));
    C[id].hsh = calc(t,len);
}

bool cmp(char *s,char *t,int len) {
    for(int i = 1 ; i <= len ; ++i) {
        if(s[i] != t[i]) return s[i] < t[i];
    }
    return 0;
}
int sap(int u,int aug) {
    if(u == T) return aug;
    int flow = 0;
    for(int i = last[u] ; i ; i = E[i].next) {
        int v = E[i].to;
        if(dis[v] + 1 == dis[u]) {
            int t = sap(v,min(aug - flow,E[i].cap));
            flow += t;
            E[i].cap -= t;
            E[i ^ 1].cap += t;
            if(aug == flow) return flow;
            if(dis[S] >= T) return flow;
        }
    }
    --gap[dis[u]];if(!gap[dis[u]]) dis[S] = T;++gap[++dis[u]];last[u] = head[u];
    return flow;
}
void Init() {
    read(N);read(M);
    for(int i = 1 ; i <= N ; ++i) read(H[i]);
    for(int i = 1 ; i <= M ; ++i) read(L[i]);
    for(int i = 1 ; i <= N ; ++i) scanf("%s",s[i] + 1);
    memset(head,0,sizeof(head));sumE = 1;
    hash_list.clear();
    memset(rev,0,sizeof(rev));revcnt = 0;
    memset(isSmall,0,sizeof(isSmall));
    memset(dis,0,sizeof(dis));
    memset(gap,0,sizeof(gap));

}
void Solve() {
    Init();
    char tmp[75];
    memset(tmp,0,sizeof(tmp));
    int tot = 0;
    cnt = 0;
    for(int i = 1 ; i <= N ; ++i) {
        tot = 0;
        for(int j = 1 ; j <= M ; ++j) {
            if(s[i][j] == '_') {
                if(tot) {
                    Insert(++cnt,tmp,tot);
                    reverse(tmp + 1,tmp + tot + 1);
                    Insert(++cnt,tmp,tot);
                }
                tot = 0;
            }
            else tmp[++tot] = s[i][j];
        }
        if(tot) {
            Insert(++cnt,tmp,tot);
            reverse(tmp + 1,tmp + tot + 1);
            Insert(++cnt,tmp,tot);
        }
    }
    for(int j = 1 ; j <= M ; ++j) {
        tot = 0;
        for(int i = 1 ; i <= N ; ++i) {
            if(s[i][j] == '_') {
                if(tot) {
                    Insert(++cnt,tmp,tot);
                    reverse(tmp + 1,tmp + tot + 1);
                    Insert(++cnt,tmp,tot);
                }
                tot = 0;
            }
            else tmp[++tot] = s[i][j];
        }
        if(tot) {
            Insert(++cnt,tmp,tot);
            reverse(tmp + 1,tmp + tot + 1);
            Insert(++cnt,tmp,tot);
        }
    }
    sort(C + 1,C + cnt + 1);
    cnt = unique(C + 1,C + cnt + 1) - C - 1;
    for(int i = 1 ; i <= cnt ; ++i) {
        hash_list[C[i].hsh] = i;
    }
    for(int i = 1 ; i <= cnt ; ++i) {
        memcpy(tmp,C[i].s,sizeof(tmp));
        int l = strlen(tmp + 1);
        reverse(tmp + 1,tmp + l + 1);
        if(calc(tmp,l) == C[i].hsh) {op[i] = i;rev[i] = 1;++revcnt;}
        else if(cmp(C[i].s,tmp,l)) {
            op[i] = hash_list[calc(tmp,l)];
            op[op[i]] = i;
            isSmall[i] = 1;isSmall[op[i]] = 0;
            addtwo(i,op[i],2);
        }
    }
    S = cnt + N + M + 1;T = S + 1;
    for(int i = 1 ; i <= N ; ++i) {
        W.clear();
        tot = 0;
        for(int j = 1 ; j <= M ; ++j) {
            if(s[i][j] == '_') {
                if(tot) {
                    int t = hash_list[calc(tmp,tot)];
                    if(!rev[t]) W.pb(t);
                }
                tot = 0;
            }
            else tmp[++tot] = s[i][j];
        }
        if(tot) {int t = hash_list[calc(tmp,tot)];if(!rev[t]) W.pb(t);}
        if(!W.size()) continue;
        sort(W.begin(),W.end());W.erase(unique(W.begin(),W.end()),W.end());
        int siz = W.size();
        if((H[i] == 1 && isSmall[W[0]]) || (H[i] == -1 && !isSmall[W[0]])) {
            addtwo(S,cnt + i,0x7fffffff);
            for(int j = 0 ; j < siz ; ++j) {
                if(isSmall[W[j]]) addtwo(cnt + i,W[j],0x7fffffff);
                else addtwo(cnt + i,op[W[j]],0x7fffffff);
            }
        }
        else if((H[i] == 1 && !isSmall[W[0]]) || (H[i] == -1 && isSmall[W[0]])) {
            addtwo(cnt + i,T,0x7fffffff);
            for(int j = 0 ; j < siz ; ++j) {
                if(!isSmall[W[j]]) addtwo(W[j],cnt + i,0x7fffffff);
                else addtwo(op[W[j]],cnt + i,0x7fffffff);
            }
        }
        else if(H[i] == 0) {
            if(!isSmall[W[0]]) {
                for(int j = 0 ; j < siz ; ++j) {
                    W[j] = op[W[j]];
                }
            }
            for(int j = 0 ; j < siz ; ++j) {
                addtwo(cnt + i,W[j],0x7fffffff);
                addtwo(op[W[j]],cnt + i,0x7fffffff);
            }
        }
    }
    for(int j = 1 ; j <= M ; ++j) {
        W.clear();
        tot = 0;
        for(int i = 1 ; i <= N ; ++i) {
            if(s[i][j] == '_') {
                if(tot) {
                    int t = hash_list[calc(tmp,tot)];
                    if(!rev[t]) W.pb(t);
                }
                tot = 0;
            }
            else tmp[++tot] = s[i][j];
        }
        if(tot) {int t = hash_list[calc(tmp,tot)];if(!rev[t]) W.pb(t);}
        if(!W.size()) continue;
        sort(W.begin(),W.end());W.erase(unique(W.begin(),W.end()),W.end());
        int siz = W.size();
        if((L[j] == 1 && isSmall[W[0]]) || (L[j] == -1 && !isSmall[W[0]])) {
            addtwo(S,cnt + N + j,0x7fffffff);
            for(int i = 0 ; i < siz ; ++i) {
                if(isSmall[W[i]]) addtwo(cnt + N + j,W[i],0x7fffffff);
                else addtwo(cnt + N + j,op[W[i]],0x7fffffff);
            }
        }
        else if((L[j] == 1 && !isSmall[W[0]]) || (L[j] == -1 && isSmall[W[0]])) {
            addtwo(cnt + N + j,T,0x7fffffff);
            for(int i = 0 ; i < siz ; ++i) {
                if(!isSmall[W[i]]) addtwo(W[i],cnt + N + j,0x7fffffff);
                else addtwo(op[W[i]],cnt + N + j,0x7fffffff);
            }
        }
        else if(L[j] == 0) {
            if(!isSmall[W[0]]) {
                for(int i = 0 ; i < siz ; ++i) {
                    W[i] = op[W[i]];
                }
            }
            for(int i = 0 ; i < siz ; ++i) {
                addtwo(cnt + N + j,W[i],0x7fffffff);
                addtwo(op[W[i]],cnt + N + j,0x7fffffff);
            }
        }
    }
    for(int i = 1 ; i <= T ; ++i) last[i] = head[i];
    int ans = revcnt;
    while(dis[S] < T) ans += sap(S,0x7fffffff);
    out(ans);enter;
}
int main() {
#ifdef ivorysi
    freopen("f1.in","r",stdin);
#endif
    e[0] = 1;
    for(int i = 1 ; i <= 100 ; ++i) e[i] = e[i - 1] * 47 % mo;
    int T;
    read(T);
    while(T--) {
        Solve();
    }
    return 0;
}