牛顿迭代法--求任意数的开n次方

牛顿迭代法是求开n次方近似解的一种方法，本文参考。

引言

假如(x^n = m)，我们需要求x的近似值。

• 我们设(f(x) = x^n - m), 那么也就是求该函数f(x)=0时与x轴的交点的值，也就是f(x)=0时方程的根。

算法介绍

感觉和物理做实验一样，先通过实验观察，再找出对应理论来解释现象。
这个算法不是推导出来的，是首先通过观察发现，再来证明推导，哈哈哈~

以下结论都是建立在f(x)二阶可导的情况下成立。

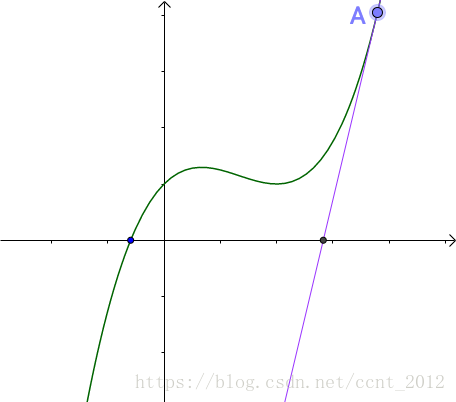
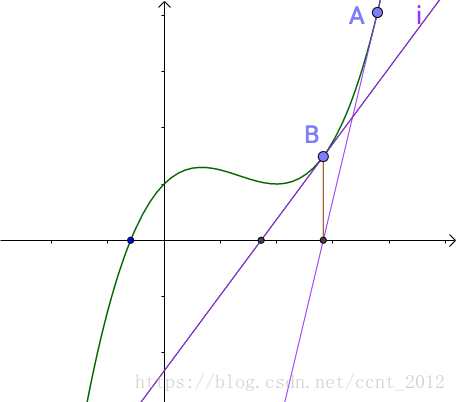
牛顿发现随便找一个曲线上的A点（为什么随便找，根据切线是切点附近的曲线的近似，应该在根点附近找，但是很显然我们现在还不知道根点在哪里），做一个切线，切线的根（就是和x轴的交点）与曲线的根，还有一定的距离。牛顿、拉弗森们想，没关系，我们从这个切线的根出发，做一根垂线，和曲线相交于B点，继续重复刚才的工作：

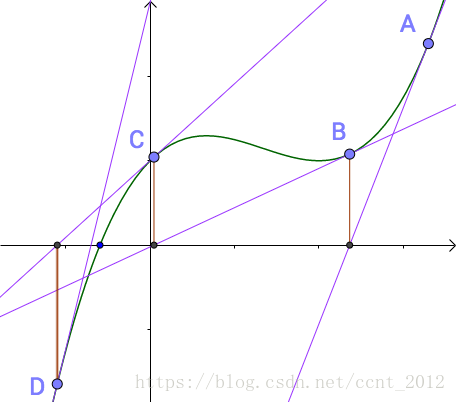
之前说过，B点比之前A点更接近曲线的根点，牛顿、拉弗森们很兴奋，继续重复刚才的工作：

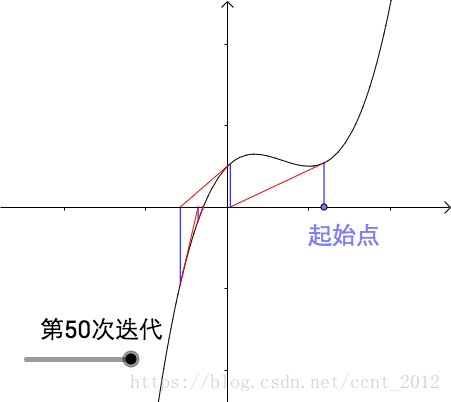
经过多次迭代后会越来越接近曲线的根（下图进行了50次迭代，哪怕经过无数次迭代也只会更接近曲线的根，用数学术语来说就是，迭代收敛了）：

总结

已知曲线方程(f(x) = x^n - m)，我们随机取一点(x_1)：

• (x_1)处切线方程为：(y - f(x_1) = f^{'}(x_1)(x - x_1))，此方程与x轴的交点为(x_2)为：
• (x_2 = x_1 - frac{f(x_1)}{f^{'}(x_1)} = x_1 - frac{x_1^n - m}{nx_1^{n-1}})
• 一直到(x_{N+1} = x_N - frac{x_N^n - m}{nx_N^{n-1}})，从而近似求解开n次方。

算法实现(go)

这是go tutorial里的一个练习，求开方。求开n次方同理。只需要改成z = z - (Pow(z,n) - m)/(n*Pow(z,(n-1)))就行了。

注意这里的z = (z + x/z)/2也就是(z = frac{z^2+x}{2z})也等于我们这里当(n=2)时，(z - frac{z^2-x}{2z})，在代码里也就是反复更新迭代z的值，缩小误差。

package main

import (
	"fmt"
	"math"
)

func Sqrt(x float64) float64 {
	z := float64(1)
	tmp := float64(0)
	for math.Abs(tmp - z) > 0.0000000001 {
		tmp = z
		z = (z + x/z)/2
	}
	return z
}

func main() {
	fmt.Println(Sqrt(2))
	fmt.Println(math.Sqrt(2))
}