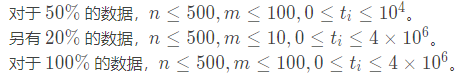[NOIP2018 普及组] 摆渡车 题解

《关于我上冬令营网课时，听说普及组考过斜率优化DP这件事》

题意理解

摆渡车往返一次要 (m) 分钟，但摆渡车可以在起点等人，故可以将往返一次的时间 (T in [m,infty ))。(但是个人都不会让他等于正无穷吧?)

求这 (n) 个人等待时间之和最小值。

设置状态

首先，观察数据范围

小数据就不说了吧

显然,可以根据时间设置状态。

设 (f_{i}) 表示前 (i) 个时间单位的最小花费。

状态转移

题上说了，摆渡车容量可以视为无限大，那么我们可以知道，摆渡车是印度产的，在时间 (i) 出发的车可以将在 (i) 及之前到站所有人都接走，花费为(sum (i-t_{k}) (t_{k}le i))。

如果在 (i)之前的某时刻 (j)，摆渡车接过一次人呢?(根据题意 (j) 应当满足 (0 le j le i-m) )。

那么就有 (f_{i}=min(f_{i},f_{j}+sum (i-t_{k})) (j < t_{k}le i)) 。

这就是状态转移方程，可以发现遍历一段时间是 (O(T)) 的，枚举断点 (j) 也是 (O(T)) 的,而计算 (sum (i-t_{k})) 是 (O(n)) 的。

这个DP时间复杂度为 (O(nT^{2}))。(恭喜你拿到我没截上屏的30分)

DP优化

优化计算

(sum (i-t_{k})) 是显然能用前缀和搞一下的:
设 (cnt_{i}) 表示时间 (i) 及之前有多少人在到达。
(sum_{i}) 表示若在 (i) 之前来的人一直在等，那么这些人一共等了多久，(sum_{i}) 可以通过 (cnt_{i}) 累加得到。

n=qr();//读入和处理cnt和sum部分
m=qr();
for(register int i=1;i<=n;i++)
{
	cnt[t=qr()]++;
	ed=max(ed,t);//ed表示最后来的人的时间
}
for(register int i=1;i<ed+m;i++)
{
	cnt[i]+=cnt[i-1];//根据前面的人数累加一下
	sum[i]+=sum[i-1]+cnt[i-1];//时间累加就是i-1~i中等待的人数
}

那么怎么通过 (cnt) 和 (sum) 计算出 (sum (i-t_{k}) (j < t_{k}le i)) 呢?

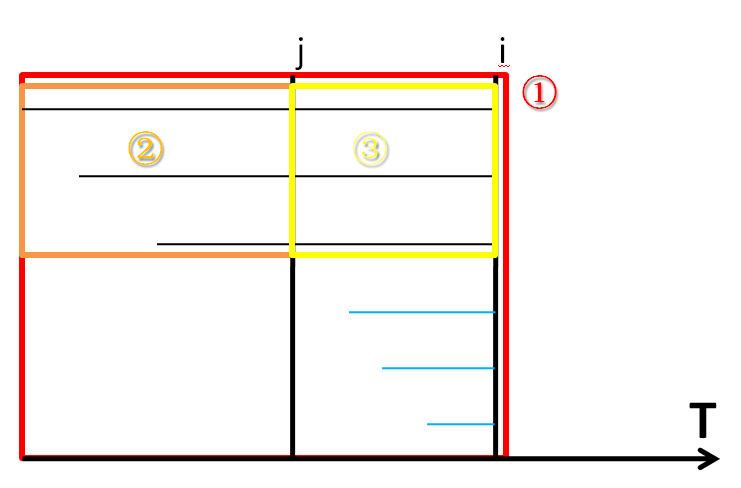
请看图。

用水平线长短及端点来表示人的等待情况，我们要求的是蓝色线的总长度。

根据我画的圈圈，(1=sum_{i}) , (2=sum_{j}) , (3=cnt_{j}*(i-j))。

那么就可以轻而易举地得到 (sum (i-t_{k}) = sum_{i}-sum_{j} - cnt_{j}*(i-j) (j < t_{k}le i))。
状态转移方程就能转化为

(f_{i}=min(f_{i},f_{j}+sum_{i}-sum_{j} - cnt_{j}*(i-j)) (jle i-m)) 。

于是复杂度愉快地变成了 (O(T^{2})) 。(现在有50pts了!)。

Code

#include<bits/stdc++.h>
#define N 1100006
#define LL long long 
using namespace std;

int n,m;
LL f[N];
int t,cnt[N],sum[N],ed;

inline int qr()
{
	char a=0;int w=1,x=0;
	while(a<'0'||a>'9'){if(a=='-')w=-1;a=getchar();}
	while(a<='9'&&a>='0'){x=(x<<3)+(x<<1)+(a^48);a=getchar();}
	return x*w;
}

int main()
{
	n=qr();//读入和处理cnt和sum部分
	m=qr();
	for(register int i=1;i<=n;i++)
	{
		cnt[t=qr()]++;
		ed=max(ed,t);//ed表示最后来的人的时间
	}
	for(register int i=1;i<ed+m;i++)//最后一班车最晚在ed+m-1时走
	{
		cnt[i]+=cnt[i-1];//根据前面的人数累加一下
		sum[i]+=sum[i-1]+cnt[i-1];//时间累加就是i-1~i中等待的人数
	}
	for(register int i=1;i<ed+m;i++)
	{
		f[i]=sum[i];//前面没有发车
		for(register int j=0;j<=i-m;j++)
			f[i]=min(f[i],f[j]+sum[i]-sum[j]-cnt[j]*(i-j));//状态转移
	}
	LL ans=0x3f3f3f3f3f3f3f3f;
	for(register int i=ed;i<ed+m;i++)//统计答案
		ans=min(ans,f[i]);
	printf("%lld
",ans);
	return 0;
}

规避无用转移

显然，每次摆渡车的往返加等待时间不会超过 (2m) ,因为该时间超过 (2m) 时,在(i-(m,2m))可以来一辆车，答案必定不会更劣。

所以，枚举 (j) 时只用枚举 ([max(0,i-2m),i-m])就可以了,复杂度变成了 (O(Tm))。

把转移改一下就有70pts了！(开O2就过了)。

Code

for(register int i=1;i<ed+m;i++)
{
	f[i]=sum[i];//前面没有发车
	for(register int j=max(i-(m<<1),0);j<=i-m;j++)
		f[i]=min(f[i],f[j]+sum[i]-sum[j]-cnt[j]*(i-j));//状态转移
}

尖端科技——斜率优化(雾)

重新看一下式子:

(f_{i}=min(f_{i},f_{j}+sum_{i}-sum_{j} - cnt_{j}*(i-j)))

把min去掉，然后移下项，可以得到:

(f_{j}+cnt_{j}*j-sum_{j}=cnt_{j}*i+f_{i}-sum_{i})

使 (y=f_{j}+cnt_{j}*j-sum_{j}) , (k=i) , (x=cnt_{j}) , (b=f_{i}-sum_{i})

于是转移方程转化愉快地为 (y=kx+b) 的点斜式形式。

这里 (x) 和 (k) 具有点调性，可以用优先队列维护下凸包。

当遍历到时间 (i) 时将 (i-m) 入队，如果队列非空进行转移，如果队列是空的话，直接当做之前没有发过车对 (f_{i}) 赋值就行了。

Code

#include<bits/stdc++.h>
#define N 9100006
#define LL long long 
#define LB long double
using namespace std;

int n,m;
LL f[N],t,cnt[N],sum[N],q[N],ed;

inline int qr()
{
	char a=0;int w=1,x=0;
	while(a<'0'||a>'9'){if(a=='-')w=-1;a=getchar();}
	while(a<='9'&&a>='0'){x=(x<<3)+(x<<1)+(a^48);a=getchar();}
	return x*w;
}

inline LB K(LL x,LL y)//计算两点间斜率
{
	return (LB) (f[y]+cnt[y]*y-sum[y]-f[x]-cnt[x]*x+sum[x])/((cnt[y]==cnt[x])?(long double)1e-9:cnt[y]-cnt[x]);
}

int main()
{
	n=qr();//读入和处理cnt和sum部分
	m=qr();
	for(register int i=1;i<=n;i++)
	{
		cnt[t=qr()]++;
		ed=max(ed,t);//ed表示最后来的人的时间
	}
	for(register int i=1;i<ed+m;i++)//最后一班车最晚在ed+m-1时走
	{
		cnt[i]+=cnt[i-1];//根据前面的人数累加一下
		sum[i]+=sum[i-1]+cnt[i-1];//时间累加就是i-1~i中等待的人数
	}
	int l=1,r=0;
	for(register int i=0;i<ed+m;i++)
	{
		if(i>=m)
		{
			int op=i-m;//将时间i-m入队
			while(l<r&&K(q[r],op)<=K(q[r-1],q[r]))//维护下凸包
				r--;
			q[++r]=op;
		}
		while(l<r&&K(q[l],q[l+1])<=(LB)i)//找到最优转移的位置
			l++;
		f[i]=sum[i];//前面没有发车
		if(l<=r)
			f[i]=min(f[i],f[q[l]]+sum[i]-sum[q[l]]-cnt[q[l]]*(i-q[l]));
	}
	LL ans=0x3f3f3f3f3f3f3f3f;
	for(register int i=ed;i<ed+m;i++)//统计答案
		ans=min(ans,f[i]);
	printf("%lld
",ans);
	return 0;
}