初级模拟电路：3-11 BJT实现电流源

回到目录

1. 恒流源

（1）简易恒流源

      用BJT晶体管可以构造一个简易的恒流源，实现电路如下：

图3-11.01 

      前面我们在射极放大电路的分压偏置时讲过，分压偏置具有非常好的稳定性，几乎不受晶体管的β参数偏移的影响，因此可以用这个分压偏置电路来实现恒流源。其电路计算方法与分压偏置也是类似的：

      基极电压V_B为：

      发射极电压V_E为：

      最终输出电流为：

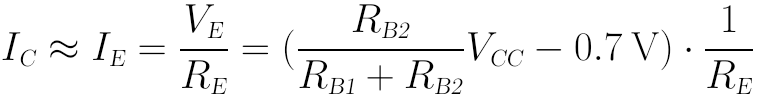
      当然，这个恒流源假设BJT晶体管工作在正常的放大区内，所以负载的阻值R_L不能太大，否则R_L上会产生过大的压降，迫使V_CE变小直至小于V_CEsat而进入饱和区，最终导致电流源失效。所以一般只能用于低成本、对输出电流要求不高的场合。

（2）改进的恒流源

      上面的简易恒流源还有个缺点，就是输出电流受V_CC的影响较大。若V_CC有波动，基极偏置电压V_B也会跟着产生波动，然后V_E也跟着波动，最终导致输出电流也会波动变化，稳定性不好。（你若要问为啥V_CC不用7805之类稳压I_C器件？这种低成本场合用一个几块钱的I_C器件是土豪么？）

      那有什么低成本的稳压器件呢？有的，答案就是齐纳二极管。改进恒流源电路如下：

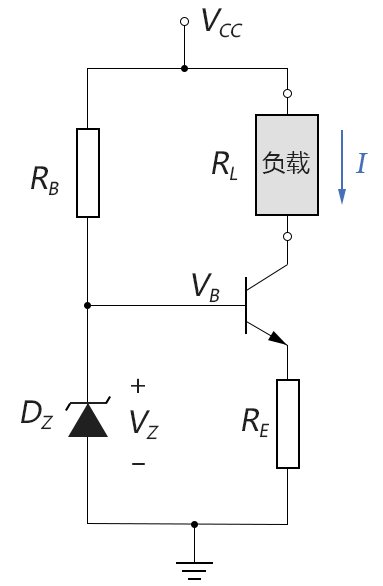
图3-11.02 

      如此，基极电压V_B可以稳定在齐纳V_Z，最终的输出电流为：

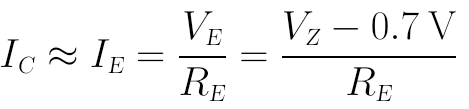
      从上式可见，输出电流表达式中没有V_CC，因此输出电流不受V_CC波动的影响。而且，齐纳二极管一般受温度影响也比较小，所以上面这个改进的恒流源电路有较好的稳定性。当然，前提还是要工作在BJT的放大区范围内才行。

（3）用pnp实现恒流源

      上面的改进恒流源还有个问题，就是负载R_L不能接地，只能悬空使用。若要使R_L能接地，必须再想办法。考虑到pnp型晶体管的电流方向相反，集电极可以接地使用，因此可用pnp型来实现恒流源，电路如下：

图3-11.03 

      上图中，计算原理和前面是一样的，只是pnp晶体管的计算方向全部相反：

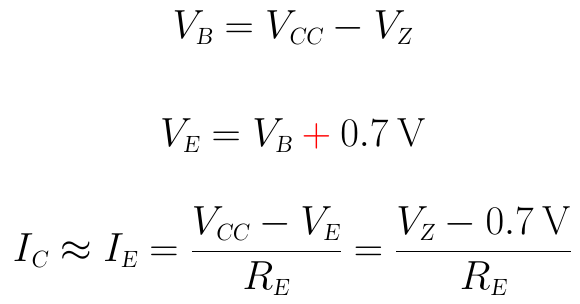
      输出电流的最终表达式与前面使用npn型晶体管的表达式是一样的。

2. 镜像电流源

      镜像电流源（Current Mirror）有时也被称为电流镜，是一种利用两个对称的晶体管产生恒流源的电路。不过，镜像电流源一般只应用于集成电路芯片内部的设计（比如运放的设计），很少在分立元件电路中使用。因为分立元器件很难找到两个放大系数一模一样的对称晶体管，而在集成电路芯片制造中做两个特性完全一致的片上晶体管是可以做到的。

      所以，一般如果你不是专门从事I_C设计的话，一般用不到这个电路。不过奇怪的是，几乎所有的模电教材都喜欢把电流镜拉出来讲一讲，好吧，那我们也讲一下吧，其实它的原理并不难。不过，这个电流镜那些个升级版：什么威尔逊（Wilson）电流镜、Wildlar电流源、比例电流镜等等……就真的不用去管了。

      电流镜的基本实现原理见下图：

图3-11.04 

      其名称由来，是因为如果你通过调节V_CC1和R_in，得到了一个原始的电流I_in；那么，在输出端可以得到一个和I_in几乎一样大小的镜像电流I_out，而不用管V_CC2和负载R_L的值（当然V_CC2和R_L不能太过分以致于超出正常工作范围）。

      其工作原理分析如下图所示：

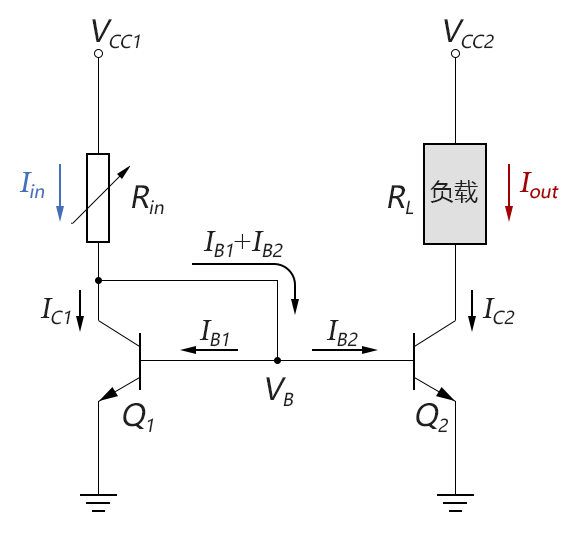
图3-11.05 

      a. 两个晶体管Q₁和Q₂的基极连接在一起，故它们的基极电压是相同的，记为V_B。

      b. 由于两个晶体管的特性是完全一致的，那么相同的基极电压V_B应该产生相同的基极电流I_B1和I_B2。

      c. 再由于两个晶体管的放大系数β也相同，那么集电极电流I_C1和I_C2也应该是相同的。

      d. 输入电流I_in=I_C1+I_B1+I_B2≈I_C1，输出电流I_out=I_C2，故输入电流I_in和输出电流I_out近似相等。

      最后的问题就是输入电流I_in怎么算。由于Q₁的集电极和基极短路，故：

      那么，输入电流I_in即为：

     

回到目录

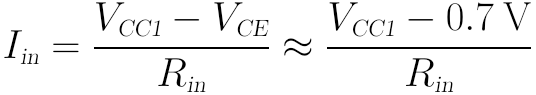
（ end of 3-11）

---