714. Best Time to Buy and Sell Stock with Transaction Fee有交易费的买卖股票

［抄题］：

Your are given an array of integers prices, for which the i-th element is the price of a given stock on day i; and a non-negative integer fee representing a transaction fee.

You may complete as many transactions as you like, but you need to pay the transaction fee for each transaction. You may not buy more than 1 share of a stock at a time (ie. you must sell the stock share before you buy again.)

Return the maximum profit you can make.

Example 1:

Input: prices = [1, 3, 2, 8, 4, 9], fee = 2
Output: 8
Explanation: The maximum profit can be achieved by:

• Buying at prices[0] = 1
• Selling at prices[3] = 8
• Buying at prices[4] = 4
• Selling at prices[5] = 9

The total profit is ((8 - 1) - 2) + ((9 - 4) - 2) = 8.

 [暴力解法]：

时间分析：

空间分析：

 [优化后]：

时间分析：

空间分析：

［奇葩输出条件］：

［奇葩corner case］：

［思维问题］：

［一句话思路］：

［输入量］：空： 正常情况：特大：特小：程序里处理到的特殊情况：异常情况（不合法不合理的输入）：

［画图］：

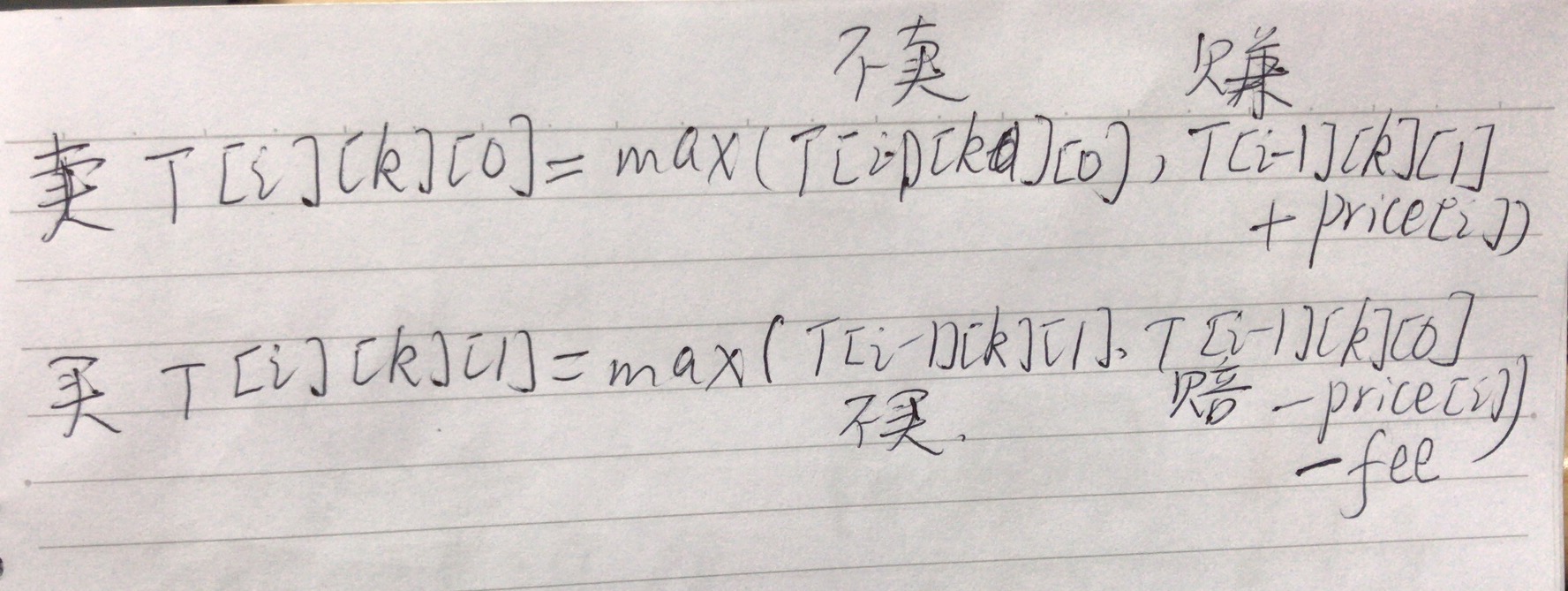
［一刷］：

［二刷］：

［三刷］：

［四刷］：

［五刷］：

  [五分钟肉眼debug的结果]：

［总结］：

基本设定是：卖会赚钱，买会赔钱

［复杂度］：Time complexity: O(n) Space complexity: O(1)

［英文数据结构或算法，为什么不用别的数据结构或算法］：

https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/discuss/108870/Most-consistent-ways-of-dealing-with-the-series-of-stock-problems

［算法思想：递归/分治/贪心］：

［关键模板化代码］：

［其他解法］：

［Follow Up］：

［LC给出的题目变变变］：

 [代码风格] ：

class Solution {
    public int maxProfit(int[] prices, int fee) {
        //ini: T_ik0, T_ik(1, T_ik0_old
        int T_ik0 = 0, T_ik1 = Integer.MIN_VALUE;
        
        //for loop
        for (int price : prices) {
            int T_ik0_old = T_ik0;
            T_ik0 = Math.max(T_ik0, T_ik1 + price);
            T_ik1 = Math.max(T_ik1, T_ik0_old - price - fee);
        }
        
        return T_ik0;
    }
}