1、哈夫曼树。Huffman Tree,中文名是哈夫曼树或霍夫曼树,它是最优二叉树,哈夫曼树,类似于算法中的二叉树,说白了哈夫曼树就是一种二叉树,只是一种最优二叉树。给定n个权值作为n个叶子结点,构造一棵二叉树,若树的带权路径长度达到最小,则这棵树被称为哈夫曼树。
2、路径。若在一棵树中存在着一个结点序列 k1,k2,……,kj, 使得 ki是ki+1 的双亲(1<=i<j),则称此结点序列是从 k1 到 kj 的路径。
3、路径长度。根据路径定义知,从 k1 到 kj 所经过的分支数称为这两点之间的路径长度,它等于路径上的结点数减1。
4、结点的权。在许多应用中,常常将树中的结点赋予一个有着某种意义的实数,我们称此实数为该结点的权,(如下面一个树中的蓝色数字表示结点的权)。
5、结点的带权路径长度。结点的带权路径长度规定为从树根结点到该结点之间的路径长度与该结点上权的乘积。
6、树的带权路径长度。如下图。其中,n表示叶子结点的数目,wi 和 li 分别表示叶子结点 ki 的权值和树根结点到 ki 之间的路径长度。

7、哈夫曼树构造规则。假设有n个权值,则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn,哈夫曼树的构造规则为。
#############################################################
1. 将w1、w2、…,wn看成是有n 棵树的森林(每棵树仅有一个结点);
2. 在森林中选出根结点的权值最小的两棵树进行合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;
3. 从森林中删除选取的两棵树,并将新树加入森林;
4. 重复(02)、(03)步,直到森林中只剩一棵树为止,该树即为所求得的哈夫曼树。
##############################################################
8、哈夫曼树的特点。
(1)对于同一组权值,所能得到的赫夫曼树不一定是唯一的。
(2)赫夫曼树的左右子树可以互换,因为这并不影响树的带权路径长度。
(3)带权值的节点都是叶子节点,不带权值的节点都是某棵子二叉树的根节点。
(4)权值越大的节点越靠近赫夫曼树的根节点,权值越小的节点越远离赫夫曼树的根节点。
(5)赫夫曼树中只有叶子节点和度为2的节点,没有度为1的节点。
(6)一棵有n个叶子节点的赫夫曼树共有2n-1个节点。
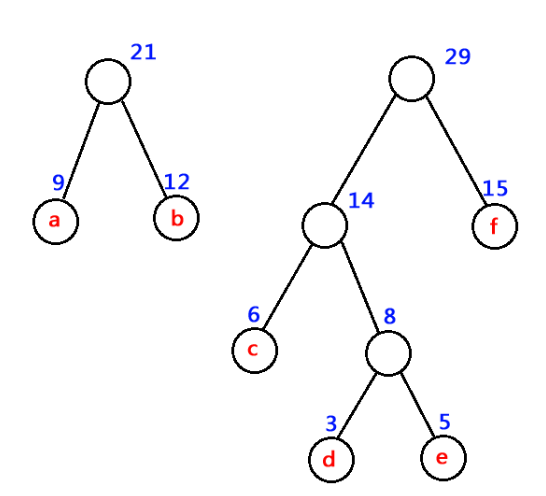
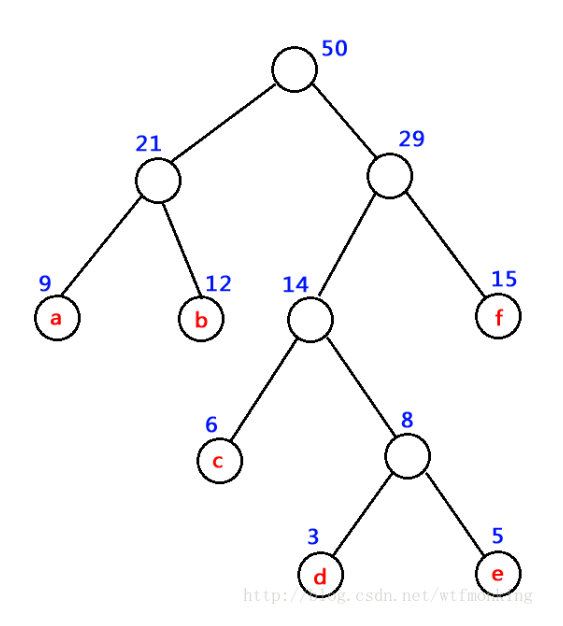
9、举例说明。为了使得到的哈夫曼树的结构尽量唯一,通常规定生成的哈夫曼树中每个结点的左子树根结点的权小于等于右子树根结点的权。权值大小排列规则是每层从左到右依次增大,即二叉搜索树结构。给定权值序列,求该序列的哈夫曼树。

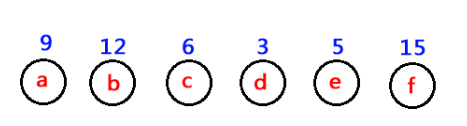
##########################################################
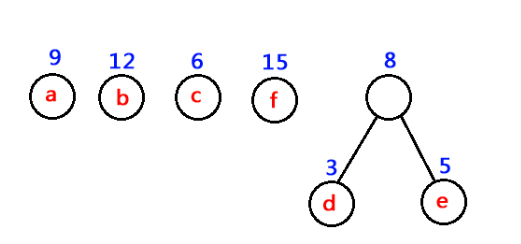
#########################################################
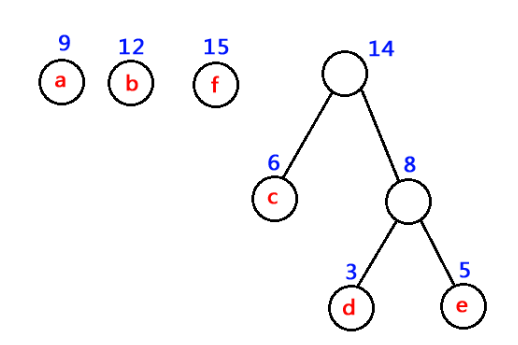
#########################################################
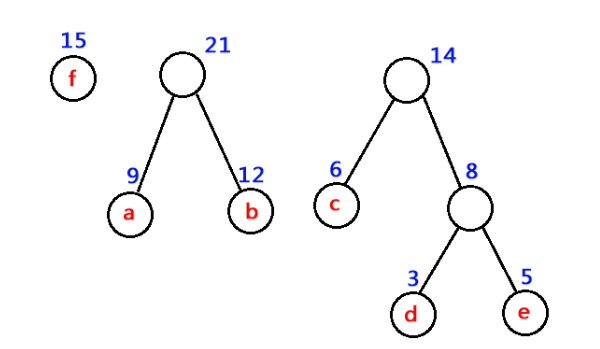
#########################################################
#########################################################
#########################################################
8、