差分约束

差分约束

1. 概念

• 如果一个系统由n个变量和m个约束条件组成，形成m个形如ai − aj ≤ k 的不等式(i,j∈[1,n], k为常数),则称其为差分约束系统。

2.引例

例如n=4,m=5，有如下五个不等式：

• x₁ - x₀ (le) 2

• x₂ - x₀ (le) 7

• x₃ - x₀ (le) 8

• x₂ - x₁ (le) 3

• x₃ - x₂ (le) 2

  很容易化简出三个不等式:

  x₃ - x₀ (le) 8

  x₃ - x₀ (le) 9

  x₃ - x₀ (le) 7

  ​

则 x₃ - x₀ 最大为7。

令x₃ = d[v], x₀ = d[u]不等式右边的值为w(u,v) 表示u到v的距离，然后对上面三个不等式移项可得：

• d[v] ≤ d[u] + w(u,v)

• 对上面的式子大家是不是很熟悉，跟我们求最短路的松弛很相像！

• 对上面的关系，如果x₁−x₀≤2，则我们就建一条x₀→x₁权值为2的有向边，我们用下图来表示：

• 

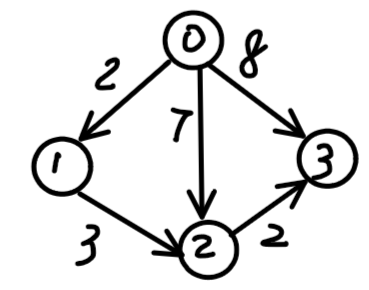
如果我们想求x_i - x_j 的最大值,只需求出x_i - x_j 的最短路,因为他们之间有多个 小于等于 的限制条件,我们必须全部满足,所以求的是最短路.

3. 问题解的存在性

​ 1.当有正权回路时,无最长路. 当有负权回路时,无最短路.

​ 2.两点间无限制条件,即不可达.

4.不等式转化

x - y (ge) w -----> y - x (le) w

x - y < w -----> x - y (le) w + 1 (x, y为整数)

x - y = w -------> x - y (le) w 且 x - y (ge) w

例题

poj1716 Integer Intervals

Description

• 区间[a,b], a，表示包含a,b连续整数的集合，给出若干个类似的区间集合，我们从每个集合中至少挑出2个元素组成一个新的集合，求满足条件新集合最小元素个数。

Input

• 第一行有一个整数n1≤n≤10000;
• 接下来n行，包含两个整数a,b(0≤a<b≤100000)，表示区间[a,b]。

Output

• 输出满足条件集合的最少元素个数。

Sample Input

4
3 6
2 4
0 2
4 7

Sample Output

4

难点是怎样把这道题和差分约束联系起来

令sum[x]为区间集合[0,x]中的被选中的元素个数。

设某个集合 [x , y]

因为要保证这个集合内至少选两个, 于是得到不等式

​ sum[ y ] - sum[ x-1 ] (ge) 2 ----------> 建边：Insert(x-1,y,2)

每个元素只有选或不选两种情况,即对于单元素的集合,选的最少为0, 最多为1

​ sum[ i + 1 ] − sum[ i ] (ge) 0 ---------> 建边：Insert(i,i+1,0)

​ sum[ i ] − sum[ i + 1 ] (ge) −1 -----------> 建边：Insert(i+1,i,-1) (这是移项转化来的)

#include <bits/stdc++.h>
const int maxn=1e4+5,Inf=0x3f3f3f3f;
using namespace std;
struct node{
	int to, dis, next;
} e[maxn*3];
int dis[maxn], vis[maxn], head[maxn], cnt[maxn];
int n, len; 
void Insert(int u, int v, int w){
    e[++len].to = v;
    e[len].dis = w;
    e[len].next = head[u];
    head[u] = len;
}
void spfa(int s, int t){//以s为起点, t条边
    for(int i=0; i<=t; i++) dis[i] = -Inf, vis[i] = 0;//初始化
    queue<int> q;
    vis[s] = 1;
    dis[s] = 0;
    q.push(s);//起点入队 
    memset(cnt, 0, sizeof(cnt));//cnt[i]表示节点i的进队次数，判环用 
    cnt[s]++;//s入队次数加一
    while(!q.empty()){		
        int u = q.front();//取出一点
	q.pop();
	vis[u]=0;        
        for(int i=head[u]; i; i=e[i].next){
            int v=e[i].to, w=e[i].dis;
            if(dis[v] < dis[u]+w){//松弛
                dis[v] = dis[u] + w;
                if(!vis[v]){
                    vis[v] = 1;
		    q.push(v);
		    cnt[v]++;
                    if(cnt[v] >= t) return;//说明有正环 
                }
            }
        }
    }
}
int main(){   
    while(~scanf("%d", &n)){
        len = 0;
	memset(head, 0, sizeof(head));//多组数据，注意初始化 
        int Max=0;//记录区间右边界的最大值 
        for(int i=1; i<=n; i++){
            int a, b; scanf("%d%d", &a, &b);
            Insert(a, b+1, 2);//注意我们这里把a, b都向右平移了一位,要不然下面处理隐含条件时插边会有负数
            Max = max(Max, b+1);//记录右边界的最大值
        }
        for(int i=0; i<=Max; i++){//处理隐含条件 
            Insert(i, i+1, 0);
	    Insert(i+1, i, -1);
        }
        spfa(0, Max);//0相当于-1
        printf("%d
", dis[Max]);
    }
    return 0;
}