T1
什么原根,矩阵乘,循环矩阵,还有什么倍增优化DP各种乱搞,说实话我没几个会的,打个暴力DP吧,还一直RE0,快自闭了,如果有缘,等我过掉他再填坑吧
T2
考思维和手推式子的好题啊,看的就是谁能发现一些别人发现不了的式子,当然了,我一个也没发现,建议自己拿张纸写一写,纯看别人题解真的看不懂
40分
emm,我考场上想出来的暴力,对于t=0倍增LCA求两点之间的距离,直接带入求b,可过第一个点,t=1最简单的办法就是高斯消元可过2,3,4,前提是高斯消元记得打对了,卡精度啊!!!
50分
多的那10分是针对一条链的,要开始推式子咯

$t=0$时,我们换个思路,由之前计算点的贡献,改为计算边的贡献,以中间点3为例,3左侧的边对于$b[3]$的贡献是每条边左侧点的$a$值之和,其实还算好想,可以自己画个样例,列一下原题的式子,拆一下合一下就可以发现它很显然了,分一下左右两侧,设$qian[i]=a[1]+a[2]+...+a[i]$,$hou[i]=a[i]+a[i+1]+...+a[n]$,也就是一个前缀一个后缀,那我们就可以得到$b[i]=qian[1]+qian[2]+...+qian[i-1]+hou[i+1]+hou[i+2]+...+hou[n]$,分别对前缀求前缀和,后缀求后缀和就可以O(n)得到了$b$数组了
$t=1$时显然依旧用刚才的式子
$b[1]=hou[2]+hou[3]+...+hou[n]$
$b[2]=qian[1]+hou[3]+hou[4]+...+hou[n]$
$b[3]=qian[1]+qian[2]+hou[4]+hou[5]+...+hou[n]$
$b[4]=qian[1]+...+qian[3]+hou[5]+hou[6]+...+hou[n]$
有好多相同的项啊,手不痒吗?不想消项吗,动手吧
$b[2]-b[1]=qian[1]-hou[2]$ $b[3]-b[2]=qian[2]-hou[3]$
$b[4]-b[3]=qian[3]-hou[4]$ ...... $b[n]-b[n-1]=qian[n-1]-hou[n]$
$qian$,$hou$数组之间有什么关系呢?显然设$SUM=a[1]+a[2]+a[3]+...+a[n]$,那么就有
$qian[i-1]+hou[i]=SUM$,$qian[i-1]=SUM-hou[i]$,带入又得到了一串式子
$b[2]-b[1]=SUM-2*hou[2]$ $b[3]-b[4]=SUM-2*hou[3]$
$b[4]-b[3]=SUM-2*hou[4]$ ...... $b[n]-b[n-1]=SUM-2*hou[n]$
又因为我们有$b[1]=hou[2]+hou[3]+...+hou[n]$,有没有想到什么?把刚才的$n-1$个式子加起来,就可以凑出两个$b[1]$了啊,好东西,$n-1$个式子做和然后消项会得到$b[n]-b[1]=(n-1)SUM-2*b[1]$,再移一下项,就可以得到$SUM=frac{b[1]+b[n]}{n-1}$,把$SUM$带回刚才的$n-1$个式子,可以求得出了$hou[1]$之外的完整$hou$数组,$hou[i]=frac{SUM-b[i]+b[i-1]}{2}$,那把求后缀和倒过来就可以求得除了$a[1]$之外的$a$数组,那$a[1]$怎么办呢,我们回到$b[2]-b[1]=qian[1]-hou[2]$,现在式子中只剩一个未知量$qian[1]$,诶,$qian[1]$不就是$a[1]$嘛,这不就搞定了
虽然我们推了这么一大片只有十分,但它对正解思路的贡献还是不可估量的
100分
正解来咯
$t=0$时,我们依旧用最初的暴力,通过一遍$DFS$跑一下$LCA$,求出$b[1]$,其实$LCA$很没劲,点$i$对$b[1]$的贡献就是$a[i]*(deep[i]-1)$,不需要$LCA$,O(n)扫一下就好了,知道了$b[1]$的话,我们可以找一找他的儿子们的$b$值和他的之间有没有什么关系,如图
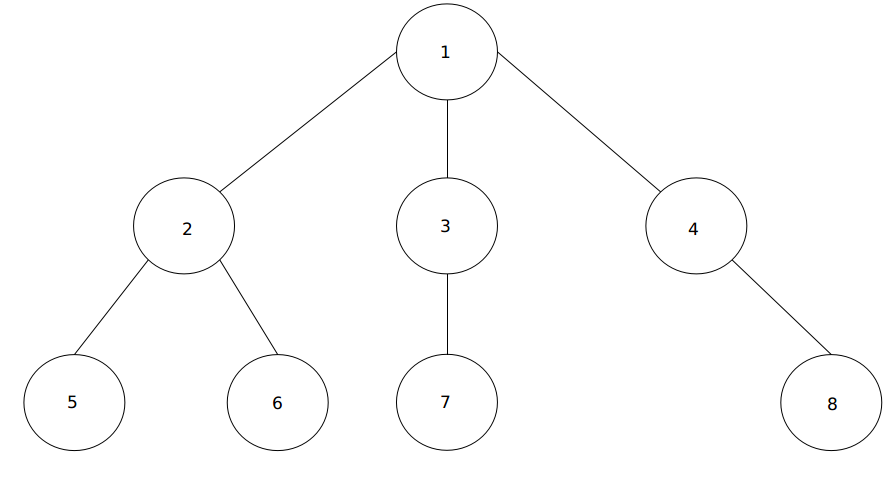
$b[1]=a[1]*0+a[2]*1+a[3]*1+a[4]*1+a[5]*2+a[6]*2+a[7]*2+a[8]*2$
$b[2]=a[1]*1+a[2]*0+a[3]*2+a[4]*2+a[5]*1+a[6]*1+a[7]*3+a[8]*3$
一一对应一下,发现了什么?2为根的子树中的点对2的贡献都少了一,其余点的贡献都多了一,当然多一少一都是对于有父子关系的点来说的,我们用$size[i]$代表以$i$为根的子树中的$a$值之和,在刚才的$DFS$中可以顺便求出,那么$b[2]=b[1]-size[2]+(size[1]-size[2])=b[1]+size[1]-2*size[2]$,我们推广到所有有父子关系的点$b[son]=b[fa]+size[1]-2*size[son]$这样的话再跑一遍$dfs$就可以求得所有的$b$了
$t=1$,想想有没有些和$b$有关的式子,当然啦,刚才写的那个不就是嘛,依旧移项,可以得到$b[son]-b[fa]=size[1]-2*size[son]$,设$c[i]=size[1]-2*size[i]$,我们就可以求得除了$c[1]$之外的整个$c$数组
现在我们继续思考,$b[1]=?$,我们想啊,一个深度为$deep$的点,肯定是有$deep-1$个父节点,那么他就被包含进了除以$1$为根之外的$deep-1$个子树中(自己作为根也是一个子树),而恰好一个点对于$b[1]$的贡献就是$a[i]*(deep[i]-1)$,所以$b[1]=size[2]+size[3]+size[4]+...+size[n]$,有没有觉得$c$数组和他有些联系?我们给除$c[1]$之外的整个$c$数组加和,$tot=(n-1)size[1]-2*(size[2]+size[3]+...+size[n])$,眼熟吧,$tot=(n-1)size[1]-2*b[1]$,那就可以得到$size[1]=frac{tot+2*b[1]}{n-1}$,那么同时你就会发现其他点的$size$也变得可求了$size[i]=frac{size[1]-c[i]}{2}$,那再跑一遍$dfs$把用$a$求$size$的式子倒过来,就可以求得所有的$a$了,当然$a[1]$这次就不特殊了,一起就求出来了
这道题怎么说呢,思维量稍大,考思维的同时,部分分还考了板子,比较全面了

1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<cstring> 5 #define int long long 6 #define maxn 100100 7 #define maxnnn 1100 8 #define maxk 19 9 using namespace std; 10 int t,fl,n,js; 11 int yz[maxn],qiu[maxn]; 12 int head[maxn],to[maxn*2],xia[maxn*2]; 13 int fa[maxn],deep[maxn],size[maxn],c[maxn]; 14 void clear() 15 { 16 js=0; 17 memset(yz,0,sizeof(yz)); memset(qiu,0,sizeof(qiu)); 18 memset(head,0,sizeof(head)); memset(to,0,sizeof(to)); 19 memset(xia,0,sizeof(xia)); memset(fa,0,sizeof(fa)); 20 memset(deep,0,sizeof(deep)); memset(size,0,sizeof(size)); 21 memset(c,0,sizeof(c)); 22 } 23 void add(int x,int y) 24 { 25 to[++js]=y; xia[js]=head[x]; head[x]=js; 26 } 27 void dfs(int x) 28 { 29 size[x]=yz[x]; 30 for(int i=head[x];i;i=xia[i]) 31 { 32 int ls=to[i]; 33 if(deep[ls]==0) 34 { 35 deep[ls]=deep[x]+1; fa[ls]=x; 36 dfs(ls); size[x]+=size[ls]; 37 } 38 } 39 } 40 void Dfs(int x) 41 { 42 for(int i=head[x];i;i=xia[i]) 43 { 44 int ls=to[i]; 45 if(fa[ls]==x) {qiu[ls]=qiu[x]-2*size[ls]+size[1]; Dfs(ls);} 46 } 47 } 48 void DFs(int x) 49 { 50 for(int i=head[x];i;i=xia[i]) 51 { 52 int ls=to[i]; 53 if(fa[ls]==0) {fa[ls]=x; c[ls]=yz[ls]-yz[x]; DFs(ls);} 54 } 55 } 56 void DFS(int x) 57 { 58 for(int i=head[x];i;i=xia[i]) 59 { 60 int ls=to[i]; 61 if(fa[ls]==x) {size[x]-=size[ls]; DFS(ls);} 62 } 63 } 64 signed main() 65 { 66 scanf("%lld",&t); 67 while(t--) 68 { 69 clear(); scanf("%lld",&n); 70 for(int i=1;i<n;++i) 71 { 72 int u,v; scanf("%lld%lld",&u,&v); 73 add(u,v); add(v,u); 74 } 75 scanf("%lld",&fl); 76 if(fl==0) 77 { 78 for(int i=1;i<=n;++i) scanf("%lld",&yz[i]); 79 deep[1]=1; dfs(1); 80 for(int i=2;i<=n;++i) qiu[1]+=yz[i]*(deep[i]-deep[1]); 81 Dfs(1); 82 for(int i=1;i<=n;++i) printf("%lld ",qiu[i]); 83 puts(""); 84 } 85 else 86 { 87 for(int i=1;i<=n;++i) scanf("%lld",&yz[i]); 88 fa[1]=-1; DFs(1); 89 int sum=0; 90 for(int i=2;i<=n;++i) sum+=c[i]; 91 size[1]=(sum+2*yz[1])/(n-1); 92 for(int i=2;i<=n;++i) size[i]=(size[1]-c[i])/2; 93 DFS(1); 94 for(int i=1;i<=n;++i) {qiu[i]=size[i]; printf("%lld ",qiu[i]);} 95 puts(""); 96 } 97 } 98 return 0; 99 }
T3
相比之下这道纯数学题反而不太难了
$opt=0$和上次的$T2visit$一毛一样,式子直接抄,而且这次还友好的不需要$CRT$了,直接求阶乘和逆元就可以
$opt=1$这是个卡特兰数,我看出来了,很开心,因为只在一条轴的一半上走,向右看作入栈,向左看作出栈,就是卡特兰数的基础模型
$opt=2$考试推了半个小时也没推出式子来,且忘了可以先打表找规律之类的,最后暴力没打完,死了,考后题解没看懂,所以选择了$DP$解决,由于空间不允许,所以我选择了把一个三维数组,拆成了两个二维数组和一个一维数组,不过可能换个题就不可用了
$opt=3$这次是组合数+卡特兰,我们假设选$i$步在竖直方向上走,那首先就会出现一个$C_n^i$,然后由于有不超过原点的限制,所以还是进出栈模型,由于算是有两个方向,所以是两个卡特兰数相乘,最终结果为$C_n^i*cat(frac{i}{2})*cat(frac{n-i}{2})$,看见$frac{}{2}$没,记得保证偶数啊

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #define ll long long 5 #define maxn 100100 6 #define maxx 1100 7 using namespace std; 8 const long long mod=1e9+7; 9 int n,typ; 10 ll ans; 11 ll jc[maxn*2],ny[maxn*2],as[maxx]; 12 ll ss[maxx][maxx*2],sp[maxx][maxx*2]; 13 ll ksm(ll a,ll b,ll c) 14 { 15 ll ans=1; a=a%c; 16 while(b) 17 { 18 if(b&1) ans=(ans*a)%c; 19 b=b>>1; a=(a*a)%c; 20 } 21 return ans%c; 22 } 23 void work1() 24 { 25 for(int u=0;u<=n/2;++u) 26 { 27 int l=n/2-u; 28 ans=(ans+(((((jc[n]*ny[u])%mod*ny[u])%mod)*ny[l]%mod)*ny[l])%mod)%mod; 29 } 30 printf("%lld ",ans%mod); 31 } 32 void work2() 33 { 34 n=n/2; 35 ans=(((((jc[2*n]*ny[n])%mod*ny[n])%mod*jc[n])%mod)*ny[n+1])%mod; 36 printf("%lld ",ans%mod); 37 } 38 void work3() 39 { 40 as[0]=1; 41 for(int o=1;o<=n;++o) 42 { 43 for(int i=0;i<=2*n;++i) 44 { 45 if(i==n) 46 { 47 as[o]=(as[o]+ss[o-1][n-1])%mod; as[o]=(as[o]+ss[o-1][n+1])%mod; 48 as[o]=(as[o]+sp[o-1][n-1])%mod; as[o]=(as[o]+ss[o-1][n+1])%mod; 49 } 50 else 51 { 52 if(i-1!=n) 53 { 54 if(i-1>=0) 55 { 56 ss[o][i]=(ss[o][i]+ss[o-1][i-1])%mod; 57 sp[o][i]=(sp[o][i]+sp[o-1][i-1])%mod; 58 } 59 } 60 else {ss[o][i]=(ss[o][i]+as[o-1])%mod; sp[o][i]=(sp[o][i]+as[o-1])%mod;} 61 if(i+1!=n) 62 { 63 ss[o][i]=(ss[o][i]+ss[o-1][i+1])%mod; 64 sp[o][i]=(sp[o][i]+sp[o-1][i+1])%mod; 65 } 66 else {ss[o][i]=(ss[o][i]+as[o-1])%mod; sp[o][i]=(sp[o][i]+as[o-1])%mod;} 67 } 68 } 69 } 70 printf("%lld ",as[n]%mod); 71 } 72 void work4() 73 { 74 for(int i=0;i<=n;i+=2) 75 { 76 ll ls1=((jc[n]*ny[i])%mod*ny[n-i])%mod; 77 ll ls2=((((jc[i]*ny[i/2])%mod*ny[i/2])%mod*jc[i/2])%mod*ny[i/2+1])%mod; 78 ll ls3=((((jc[n-i]*ny[(n-i)/2])%mod*ny[(n-i)/2])%mod*jc[(n-i)/2])%mod*ny[(n-i)/2+1])%mod; 79 ans=(ans+(((ls1*ls2)%mod)*ls3)%mod)%mod; 80 } 81 printf("%lld ",ans%mod); 82 } 83 int main() 84 { 85 scanf("%d%d",&n,&typ); jc[0]=1; 86 for(int i=1;i<=2*n;++i) jc[i]=(jc[i-1]*i)%mod; 87 ny[2*n]=ksm(jc[2*n],mod-2,mod); 88 for(int i=2*n;i>=1;--i) ny[i-1]=(ny[i]*i)%mod; 89 if(typ==0) work1(); 90 else if(typ==1) work2(); 91 else if(typ==2) work3(); 92 else work4(); 93 return 0; 94 }
