欢迎关注WX公众号:【程序员管小亮】
专栏——深度学习入门笔记
声明
1)该文章整理自网上的大牛和机器学习专家无私奉献的资料,具体引用的资料请看参考文献。
2)本文仅供学术交流,非商用。所以每一部分具体的参考资料并没有详细对应。如果某部分不小心侵犯了大家的利益,还望海涵,并联系博主删除。
3)博主才疏学浅,文中如有不当之处,请各位指出,共同进步,谢谢。
4)此属于第一版本,若有错误,还需继续修正与增删。还望大家多多指点。大家都共享一点点,一起为祖国科研的推进添砖加瓦。
深度学习入门笔记(九):深度学习数据处理
1、训练集,验证集,测试集

在深度学习的实践中,如何配置 训练、验证 和 测试 数据集?比例是怎么样的?哪一个数据集应该更多一些?这个过程中能否做出正确决策,会在很大程度上决定我们能否创建高效的神经网络。训练神经网络时,需要做出很多决策,例如:
-
神经网络分多少层
-
每层含有多少个隐藏单元
-
学习速率是多少
-
各层采用哪些激活函数

除了上面说的这些超参数之外,能否创建一个高质量的 训练集,验证集 和 测试集 也有助于提高循环的效率。
这是个什么循环?我们在 深度学习入门笔记(七):深层神经网络 中说过这个循环,是 Idea—Code—Experiment—Idea 这个大循环,好的数据集可以提高这个过程的循环效率,从而加快实验的进程,更快更好地得到最后的记过。
假设整个数据集用一个长方形表示,我们通常会将这些数据划分成几部分:一部分作为 训练集;一部分作为 简单交叉验证集,有时也称之为 验证集,一般都叫它 验证集(dev set),其实都是同一个概念;最后一部分则作为 测试集。
接下来,我们开始对 训练集 执行算法,通过 验证集 选择最好的模型,经过充分验证,选定最终模型,然后就可以在 测试集 上进行评估了,为了无偏评估算法的运行状况,选用的测试集应该是没有参与过训练过程的!!!
在机器学习发展的小数据量时代,常见做法是 将所有数据三七分,就是人们常说的70%训练集,30%测试集。如果明确设置了 验证集,也可以按照 60%训练集,20%验证集和20%测试集 来划分。这是这些年机器学习领域普遍认可的最好的实践方法。

如果只有100条,1000条或者1万条数据,那么上述比例划分是非常合理的。但是在大数据时代,现在的数据量可能是百万级别,那么 验证集 和 测试集 占数据总量的比例会趋向于变得更小。因为 验证集 的目的就是验证不同的算法,检验哪种算法更有效,因此,验证集 只要足够大到能评估不同的算法,比如2个甚至10个不同算法,并迅速判断出哪种算法更有效,不需要拿出20%的数据作为验证集。

比如现在有100万条数据,那么取1万条数据便足以进行评估即可,找出其中表现最好的1-2种算法。同样地,根据最终选择的分类器,测试集 的主要目的是正确评估分类器的性能,所以,如果拥有百万数据,我们只需要1000条数据,便足以评估单个分类器,并且准确评估该分类器的性能。
- 假设我们有100万条数据,其中1万条作为 验证集,1万条作为 测试集,100万里取1万,比例是1%,即:训练集占98%,验证集和测试集各占1%。
- 对于数据量过百万的应用,训练集可以占到99.5%,验证和测试集各占0.25%,或者验证集占0.4%,测试集占0.1%。
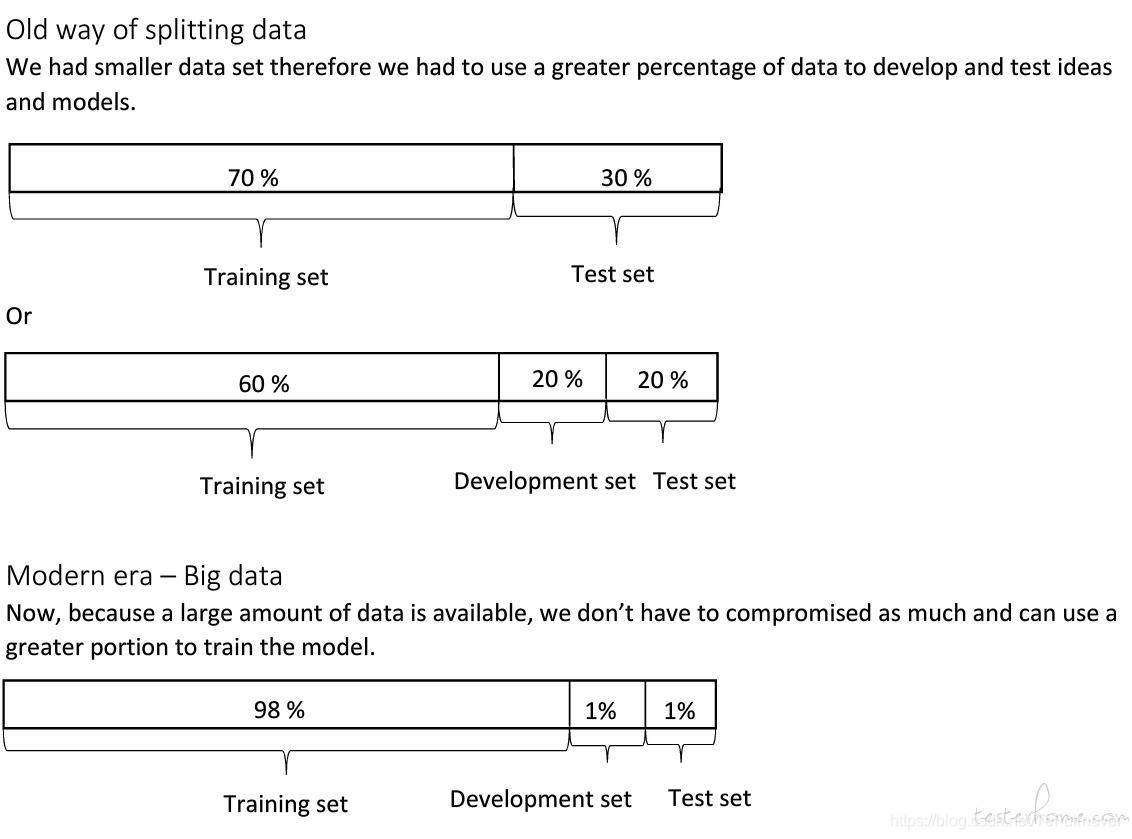
总结一下,在机器学习中,我们通常将样本分成 训练集,验证集 和 测试集 三部分,数据集规模相对较小,适用传统的划分比例,数据集规模较大的,验证集 和 测试集 要小于数据总量的20%或10%,具体要怎么做?别着急,后面会给出如何划分验证集和测试集的具体指导。
现代深度学习的另一个趋势是 越来越多的人在训练和测试集分布不匹配的情况下进行训练,假设你要构建一个用户可以上传大量图片的应用程序,目的是找出并呈现所有猫咪图片,可能你的用户都是爱猫人士,训练集可能是从网上下载的猫咪图片,而 验证集 和 测试集 是用户在这个应用上上传的猫的图片,就是说,训练集 可能是从网络上抓下来的图片,而 验证集 和 测试集 是用户上传的图片。结果许多网页上的猫咪图片分辨率很高,很专业,后期制作精良,而用户上传的照片可能是用手机随意拍摄的,像素低,比较模糊,这两类数据有所不同,针对这种情况,根据经验,建议大家要确保 验证集 和 测试集 的数据来自同一分布,学术说法就是 独立同分布(IID)。
定义:独立同分布(iid,independently identically distribution) 在概率统计理论中,指随机过程中,任何时刻的取值都为随机变量,如果这些随机变量服从同一分布,并且互相独立,那么这些随机变量是独立同分布。

但由于深度学习算法需要 大量的训练数据,为了获取更大规模的训练数据集,我们可以采用当前流行的各种创意策略,例如,网页抓取,代价就是训练集数据与验证集和测试集数据有可能不是来自同一分布。但只要遵循这个经验法则,你就会发现机器学习算法会变得更快。
最后一点,就算没有测试集也不要紧,测试集的目的是对最终所选定的神经网络系统做出无偏估计,如果不需要无偏估计,也可以不设置测试集。所以如果只有 验证集,没有 测试集,我们要做的就是,在 训练集 上训练,尝试不同的模型框架,在 验证集 上评估这些模型,然后迭代并选出适用的模型。因为 验证集 中已经涵盖测试集数据,其不再提供无偏性能评估。当然,如果你不需要无偏估计,那就再好不过了。
在机器学习中,如果只有一个 训练集 和一个 验证集,而没有独立的测试集,遇到这种情况,训练集 还被人们称为 训练集,而 验证集 则被称为 测试集,不过在实际应用中,人们只是把 测试集 当成 简单交叉验证集 使用,并没有完全实现该术语的“验证”功能,因为他们把 验证集 数据过度拟合到了 测试集 中。
如果某团队跟你说他们只设置了一个 训练集 和一个 测试集,你要小心了!!!要想他们是不是真的有 训练验证集,因为他们把 验证集 数据过度拟合到了 测试集 中,让这些团队改变叫法,改称其为 训练验证集,而不是 训练测试集,可能不太容易。即便 训练验证集 在专业用词上更准确。实际上,如果你不需要无偏评估算法性能,那么这样是可以的。
所以说,搭建 训练验证集 和 测试集 能够加速神经网络的集成,也可以更有效地衡量算法地 偏差 和 方差,从而帮助我们更高效地选择合适方法来优化算法。
有的同学还是不懂这个数据集都是什么意思,尤其是验证集和测试集,来看一个例子:
- 训练集——课本;学生学习并根据课本里的内容来掌握知识。
- 验证集——作业;通过学生完成作业的水平,可以知道学习质量的好坏。
- 测试集——考试;通过学生考试的结果(考的题是平常都没有见过的),来考察学生举一反三的能力,也可以知道学习质量的好坏。
例子不是特别严谨,只是提供一种理解的方式!
2、偏差,方差
如果你细心的话,就会注意到,几乎所有机器学习从业人员都期望深刻理解 偏差 和 方差(我也是这样的=-=),这两个概念易学难精,即使你认为已经理解了 偏差 和 方差 的基本概念,却总有一些意想不到的新东西出现。关于深度学习的误差问题,另一个趋势是对 偏差 和 方差 的权衡研究甚浅,你可能听说过这两个概念,但深度学习的误差很少权衡二者,我们总是分别考虑 偏差 和 方差,却很少放在一起。

如上图,假设这就是数据集,如果想要对这个数据集拟合一条直线,可能得到一个逻辑回归拟合,但它并不能很好地拟合该数据,这是 高偏差(high bias) 的情况,我们称之为 欠拟合(underfitting)。
相反的如果我们拟合一个非常复杂的分类器,比如深度神经网络或含有隐藏单元的神经网络,可能就非常适用于这个数据集,但是这看起来也不是一种很好的拟合方式,即 高方差(high variance) 的情况,我们称之为 过拟合(overfitting)。
在两者之间,可能还有一些像下面三个图的中间图这样的,复杂程度适中,数据拟合适度的分类器,这个数据拟合看起来更加合理,我们称之为 适度拟合(just right),是介于 过拟合 和 欠拟合 中间的一类。

在这样一个只有 和 两个特征的二维数据集中,我们可以绘制数据,将 偏差 和 方差 可视化。在多维空间数据中,绘制数据和可视化分割边界无法实现,但我们可以通过几个指标,来研究 偏差 和 方差。

还是沿用猫咪图片分类这个例子(深度学习入门笔记(一):深度学习引言),左边一张是猫咪图片,右边一张不是。理解 偏差 和 方差 的两个关键数据是 训练集误差(Train set error) 和 验证集误差(Dev set error),为了方便论证,假设我们可以辨别图片中的小猫,用肉眼识别的结果几乎是不会出错的。
假定 训练集误差 是1%,为了方便论证,假定 验证集误差 是11%,可以看出 训练集 设置得非常好,而 验证集 设置相对较差,可能是 过度拟合 了 训练集,在某种程度上,验证集 并没有充分利用 交叉验证集 的作用,像这种情况,我们称之为 高方差。
通过查看 训练集误差 和 验证集误差,我们便可以诊断算法是否具有 高方差。也就是说衡量 训练集 和 验证集误差 就可以得出不同结论。
假设 训练集误差 是15%,我们把 训练集误差 写在首行,验证集误差 是16%。算法并没有在 训练集 中得到很好训练,如果训练数据的拟合度不高,就是数据 欠拟合,就可以说这种算法 偏差比较高。相反,它对于 验证集 产生的结果却是合理的,验证集 中的错误率只比训练集的多了1%,所以这种算法 偏差高,因为它甚至不能拟合训练集,这与下图的最左边的图片相似。

再举一个例子,训练集误差 是15%,偏差相当高,但是,验证集 的评估结果更糟糕,错误率达到30%,在这种情况下,我会认为这种算法 偏差高,因为它在 训练集 上结果不理想,而且 方差也很高,这是 方差偏差都很糟糕 的情况,不要觉得 方差 好像是更高。。。
再看最后一个例子,训练集误差 是0.5%,验证集误差 是1%,用户看到这样的结果会很开心,猫咪分类器只有1%的错误率,偏差和方差都很低。
这些分析都是基于假设预测的,假设人眼辨别的错误率接近0%,一般来说,最优误差 也被称为 贝叶斯误差,所以,最优误差 接近0%。但是如果 最优误差 或 贝叶斯误差 非常高,比如时15%。再看看这个分类器(训练误差15%,验证误差16%),15%的错误率对 训练集 来说也是非常合理的,偏差不高,方差也非常低。
小结一下:要看我们的最优误差是多少,才能判断你的 偏差 和 方差 !!!

当所有分类器都不适用时,如何分析 偏差 和 方差 呢?比如,图片很模糊,即使是人眼,或者没有系统可以准确无误地识别图片,在这种情况下,最优误差 会更高,那么分析过程就要做些改变了。
以上分析的前提都是 假设基本误差很小,训练集和验证集数据来自相同分布,如果没有这些假设作为前提,分析过程更加复杂,后面会讨论这个问题的。
有一个疑问出现了,偏差 和 方差 都高是什么样子呢?这种情况对于两个衡量标准来说都是非常糟糕的。
之前讲过,这样的分类器,会产生 高偏差,偏差高 是因为它几乎是一条线性分类器,并未拟合数据,像这种接近线性的分类器,数据拟合度低。

但是如果稍微改变一下分类器,用紫色笔画出,它会 过度拟合 部分数据。用紫色线画出的分类器具有 高偏差 和 高方差:偏差高 是因为它几乎是一条线性分类器,并未拟合数据;方差高 是因为它灵活性太高以致拟合了这两个错误样本和中间这些活跃数据。

这看起来有些不自然,从两个维度数据上看,怎么看都不太自然,但对于高维数据,有些数据区域 偏差高,有些数据区域 方差高,所以看起来就不会那么牵强了。
总结:拟合地好是最好的,但是过拟合是方差大,欠拟合是偏差大,还有一种可能是两个差都大!!!
3、机器学习基础
下图就是在训练神经网络用到的基本方法:(尝试这些方法,可能有用,可能没用)
吴恩达老师手稿:

初始模型训练完成后,首先要知道算法的 偏差 高不高,如果 偏差较高,试着评估 训练集 或 训练数据 的性能。如果 偏差 的确很高,甚至无法拟合训练集,那么要做的就是选择一个新的网络,比如含有更多隐藏层或者隐藏单元的网络,或者花费更多时间来训练网络,或者尝试更先进的优化算法,后面会讲到。训练学习算法时,要不断尝试这些方法,直到解决掉 偏差 问题,这是 最低标准,反复尝试,直到可以拟合数据为止,至少能够拟合训练集。当然你也可以尝试其他方法,可能有用,也可能没用。
博主注:训练神经网络时,建议先尽量过拟合,再通过各种方法解决过拟合的问题,这样的代价更小,成功的可能性更大。
如果网络足够大,通常可以很好地拟合 训练集,实在不行的话,只要你能扩大网络规模,即使图片很模糊,至少可以很好地拟合 训练集,或者 过拟合 训练集。一旦 偏差 降低到可以接受的数值,检查一下 方差 有没有问题,为了评估 方差,我们要查看 验证集 的性能,从一个性能理想的 训练集 推断出 验证集 的性能是否也理想,如果 方差高,最好的解决办法就是采用更多数据,让网络见识到更多的数据类型,拥有更强的拟合泛化能力。如果你能做到这一点,会有一定的帮助,但有时候,无法获得更多数据,我们也可以尝试通过 正则化 来减少 过拟合,这个下一个笔记会讲。
有同学抱怨麻烦,没法子,有时候我们不得不反复尝试这些操作,但是,如果能找到更合适的神经网络框架,有时它可能会一箭双雕,同时减少 方差 和 偏差。如何实现呢?想系统地说出做法很难,总之就是不断重复尝试,直到找到一个 低偏差,低方差 的框架,这时你就成功了。
有两点需要特别注意:
第一点,高偏差 和 高方差 是两种不同的情况,所以后续要尝试的方法也可能完全不同,通常会用 训练验证集 来诊断算法是否存在 偏差 或 方差 问题,然后根据结果选择尝试部分方法。举个例子,如果算法存在 高偏差 问题,准备更多训练数据其实也没什么用处,至少这不是更有效的方法,所以一定要清楚存在的问题是 偏差 还是 方差,还是两者都有问题,明确这一点有助于我们选择出最有效的方法,不然就相当于做无用功,瞎忙乎。
第二点,在机器学习的初期阶段,关于所谓的 偏差方差权衡 的讨论屡见不鲜,原因是能尝试的方法有很多。可以增加 偏差,减少 方差,也可以减少 偏差,增加 方差,但是在深度学习的早期阶段,没有太多工具可以做到只减少 偏差 或 方差 却不影响到另一方。然而当前的深度学习和大数据时代,只要持续训练一个更大的网络,只要准备了更多数据,那么也并非只有这两种情况,简单情况下,只要 正则 适度,通常构建一个更大的网络便可以,在不影响 方差 的同时减少 偏差,而采用更多数据通常可以在不过多影响 偏差 的同时减少 方差。这两步实际要做的工作是:训练网络,选择网络或者准备更多数据,现在有了一个可以做到在减少 偏差 或 方差 的同时,不对另一方产生过多不良影响的工具。这就是深度学习对监督式学习大有裨益的一个重要原因,也是不用太过关注如何 平衡偏差和方差 的一个重要原因。
最终,我们会得到一个非常规范化的网络!!!
补充
正则化,是一种非常实用的减少 方差 的方法,正则化 时会出现 偏差方差权衡 问题,偏差 可能略有增加,但是如果网络足够大的话,增幅通常不会太高,从而完美地解决 方差大 的问题。
推荐阅读
- 深度学习入门笔记(一):深度学习引言
- 深度学习入门笔记(二):神经网络基础
- 深度学习入门笔记(三):求导和计算图
- 深度学习入门笔记(四):向量化
- 深度学习入门笔记(五):神经网络的编程基础
- 深度学习入门笔记(六):浅层神经网络
- 深度学习入门笔记(七):深层神经网络
- 深度学习入门笔记(八):深层网络的原理
- 深度学习入门笔记(九):深度学习数据处理
- 深度学习入门笔记(十):正则化
- 深度学习入门笔记(十一):权重初始化
- 深度学习入门笔记(十二):深度学习数据读取
- 深度学习入门笔记(十三):批归一化(Batch Normalization)
- 深度学习入门笔记(十四):Softmax
- 深度学习入门笔记(十五):深度学习框架(TensorFlow和Pytorch之争)
- 深度学习入门笔记(十六):计算机视觉之边缘检测
- 深度学习入门笔记(十七):深度学习的极限在哪?
- 深度学习入门笔记(十八):卷积神经网络(一)
- 深度学习入门笔记(十九):卷积神经网络(二)
- 深度学习入门笔记(二十):经典神经网络(LeNet-5、AlexNet和VGGNet)
参考文章
- 吴恩达——《神经网络和深度学习》视频课程