2018-07-10 18:30:19
贪心法就是遵循某种规则,不断贪心的选取当前最优策略的算法设计方法。一般来说,如果一个问题可以使用贪心法来解决的话,那么它通常是非常高效的。
贪心法困难之处在于:
1)最优策略的选择;
2)算法有效性的证明。
一、区间问题
问题描述:
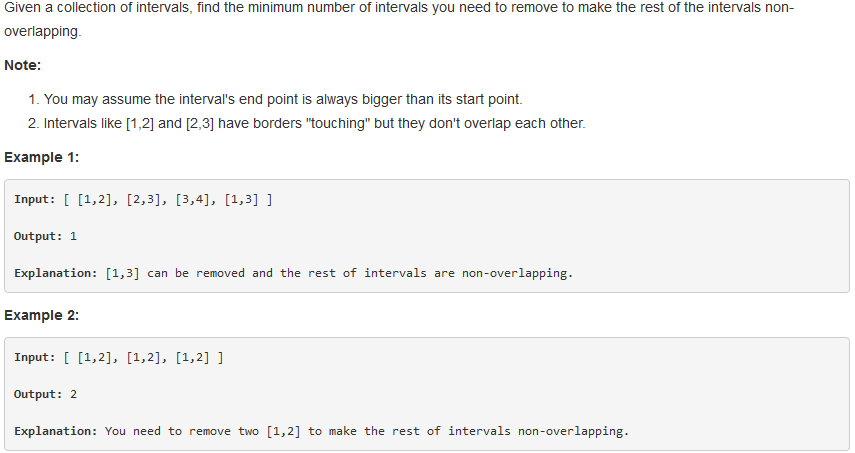
问题求解:
这个问题其实是区间问题的变种题了,问题中需要求的是最少需要剔除多少区间,换言之就是求最大的相容区间数目。
区间问题是一个典型的可以使用贪心算法予以解决的问题,使用贪心算法,在未排序的情况下,时间复杂度为O(nlogn),若已经排序好,则时间复杂度为O(n)。
这里贪心算法使用的策略是:
在可选的工作中,每次都选择结束时间最早的工作。
证明:
结束时间越早,之后可选的工作就越多。这是该算法能够正确处理问题的一个直观的解释。但是这不是一个严格的证明。我们可以通过一下的方法来证明。
(1)与其他选择方案相比,该算法在选取相同数量的更早开始的工作时,其最终的结束时间不会比其他方案更晚。
(2)所以不存在选取更多工作的选择方案。
可以使用数学归纳法或者反证法来进行证明。
public int eraseOverlapIntervals(Interval[] intervals) {
if (intervals.length == 0) return 0;
Arrays.sort(intervals, new Comparator<Interval>() {
@Override
public int compare(Interval o1, Interval o2) {
return o1.end - o2.end;
}
});
int cnt = 1;
int end = intervals[0].end;
for (int i = 1; i < intervals.length; i++) {
if (intervals[i].start >= end) {
cnt++;
end = intervals[i].end;
}
}
return intervals.length - cnt;
}
二、字典序最小问题
问题描述:
给定长度为N的字符串S,要构造一个长度为N的字符串T。起初,T是一个空串,随后反复进行下列任意操作。
- 从S的头部删除一个字符,加到T尾部
- 从S的尾部删除一个字符,加到T尾部
目标是要构造字典序尽可能小的字符。
问题求解:
字典序的大小和前面字符的大小相关,因此T中前面的字符越小则最终结果的字典序越小。
可以制定如下的策略:
不断取S的开头和末尾中较小的一个字符放到T的末尾;
如果出现开头和末尾字符大小相同的情况,则需要按照字典序比较S和S的反转序列S‘
如果S较小,则将头部字符添加到T中;
如果S’较小,则将尾部字符添加到T中。
public class BestCowLine {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
StringBuffer sb = new StringBuffer();
StringBuffer res = new StringBuffer();
for (int i = 0; i < n; i++) sb.append(sc.next());
int l = 0;
int r = sb.length() - 1;
while (l <= r) {
if (sb.charAt(l) < sb.charAt(r)) res.append(sb.charAt(l++));
else if (sb.charAt(r) < sb.charAt(l)) res.append(sb.charAt(r--));
else {
String s1 = sb.substring(l, r + 1);
String s2 = new StringBuffer(s1).reverse().toString();
if (s1.compareTo(s2) < 0) res.append(sb.charAt(l++));
else if (s1.compareTo(s2) > 0) res.append(sb.charAt(r--));
else {
res.append(s1);
break;
}
}
}
int idx = 0;
while (idx < res.length()) {
int i;
for (i = 0; i < 80; i++) {
System.out.print(res.charAt(idx++));
if (idx >= res.length()) break;
}
if (i == 80) System.out.println();
}
}
}
三、Saruman‘s Army
问题描述:
直线上有N个点。点i的位置是Xi。从这N个点中选择若干个,给他们加上标记。对每个点,其距离为R以内的区域里必须有标记的点。在满足这个条件下,希望能给尽量少的点添加标记。请问至少有多少点被加上标记?
问题求解:
本题也是可以通过贪心法进行高效求解的,使用的策略为:
从最左边开始考虑,对于这个点,到其距离为R的区域内必须包含带有标记的点,由于此点位于最左边,因此带有标记的点必然在右侧,显然标记点应该是从最左边的点开始,距离为R以内的最远的点。因为更左的区域没有覆盖的意义,所以应该尽量找覆盖更靠右的点。
下一步就是寻找不被这个标记点覆盖的下一个最左点,重复上述的过程。
public class SarumanArmy {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int R, n;
int[] nums;
int cnt;
while((R = sc.nextInt()) != -1) {
n = sc.nextInt();
nums = new int[n];
for (int i = 0; i < n; i++) nums[i] = sc.nextInt();
Arrays.sort(nums);
cnt = 0;
int idx = 0;
while (idx < n) {
int l = nums[idx];
while (idx < n && nums[idx] <= l + R) idx++;
cnt++;
l = nums[idx - 1];
while (idx < n && nums[idx] <= l + R) idx++;
}
System.out.println(cnt);
}
}
}
四、Fence Repair
问题描述:
农夫为了修理栅栏,需要将一块很长的木板切割成N块。准备切成的木板的长度为L1,L2,...,LN,未切割前木板的长度恰好为切割后木板长度的总和。每次切断木板时,需要的开销为这块木板的长度。例如长度为21的木板切成5,8,8三块。长度21的木板切成13和8的时候,开销为21。再将长度为13的木板切割成5,8的时候,开销为13。因此总的开销为34。请求出按照目标要求将木板切割完最小的开销是多少。
问题求解:
首先切割的方法可以是用二叉树来形象的表示,二叉树中每一个叶子节点就对应了切割出的一块木板。叶子节点的深度就对应了为了得到该木板需要的切割次数,开销的合计就是各个叶子节点的木板长度 * 节点深度。
有了以上的分析,最佳策略就是:
最短的板和次短的板的节点应该是兄弟节点。
最短的板应当是深度最深的节点之一。所以与这个节点同一深度的兄弟节点一定存在,并且由于同样是深度最深的叶子节点,所以应当对应的是次短的板。
只需要递归的对上述的板进行拼接,就可以得到结果。
public class FencerRepair {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] nums = new int[n];
for (int i = 0; i < n; i++) nums[i] = sc.nextInt();
int min1, min2;
long res = 0;
while (n > 1) {
min1 = 0;
min2 = 1;
if (nums[min1] > nums[min2]) {
int temp = min1;
min1 = min2;
min2 = temp;
}
for (int i = 2; i < n; i++) {
if (nums[i] <= nums[min1]) {
min2 = min1;
min1 = i;
}
else if (nums[i] < nums[min2]) min2 = i;
}
int t = nums[min1] + nums[min2];
res += t;
if (min1 == n - 1) {
int temp = min1;
min1 = min2;
min2 = temp;
}
nums[min1] = t;
nums[min2] = nums[n - 1];
n--;
}
System.out.println(res);
}
}
这个问题的解法作为计算霍夫曼编码的算法而被熟知。在上述算法中将木板换成字符,长度换成频度就可以了。
五、Cleaning Shifts
问题描述:
Farmer John is assigning some of his N (1 <= N <= 25,000) cows to do some cleaning chores around the barn. He always wants to have one cow working on cleaning things up and has divided the day into T shifts (1 <= T <= 1,000,000), the first being shift 1 and the last being shift T.
Each cow is only available at some interval of times during the day
for work on cleaning. Any cow that is selected for cleaning duty will
work for the entirety of her interval.
Your job is to help Farmer John assign some cows to shifts so that
(i) every shift has at least one cow assigned to it, and (ii) as few
cows as possible are involved in cleaning. If it is not possible to
assign a cow to each shift, print -1.
Input
* Lines 2..N+1: Each line contains the start and end times of the interval during which a cow can work. A cow starts work at the start time and finishes after the end time.
Output
Sample Input
3 10 1 7 3 6 6 10
Sample Output
2
问题求解:
问题实际上就是求能否使用最少的区间来完成覆盖,如果可以则输出最小的数量,如果不行,则输出-1。
使用贪心法可以解决,策略为:
每次寻找可能的下一个最大覆盖,如果不存在下一个更大的覆盖,比如出现间断等情况,则直接返回-1
编程实现的时候有几点需要注意:
1)排序的时候在开始时间相同的情况下,需要按照结束时间降序排序;
2)如果排序后的第一个开始时间不为1,则直接输出-1;
3)必须要对不存在下一个更大覆盖进行判断,如果出现了这种情况则,返回-1
public class CleaningShifts {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N, T;
N = sc.nextInt();
T = sc.nextInt();
int[][] intervals = new int[N][2];
for (int i = 0; i < N; i++) {
intervals[i][0] = sc.nextInt();
intervals[i][1] = sc.nextInt();
}
Arrays.sort(intervals, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
if (o1[0] == o2[0]) return o2[1] - o1[1];
else return o1[0] - o2[0];
}
});
int res = 1;
int end = intervals[0][1];
if (intervals[0][0] != 1) System.out.println(-1);
else {
int i = 0;
while (i < N) {
if (end >= T) break;
int idx = i;
while (i < N && intervals[i][0] <= end + 1) {
if (intervals[i][1] > intervals[idx][1]) idx = i;
i++;
}
if (intervals[idx][1] == end) break;
i = idx;
end = intervals[idx][1];
res++;
}
if (end < T) System.out.println(-1);
else System.out.println(res);
}
}
}