UGC

 

 

文章目录

    4 UGC推荐
        4.1 基于用户UGC标签进行推荐
            4.1.1 最简单的算法（SimpleTagBased）
            4.1.2 利用TF-IDF进行改进（TagBasedTFIDF和TagBasedTFIDF++）
            4.1.3 标签扩充改进
            4.1.4 基于图的推荐
        4.2 给用户推荐标签
            4.2.1 基于统计的方法
            4.2.2 基于图的标签推荐

4 UGC推荐

用户的标签行为数据集一般由(u, i, b)三元组组成，表示用户u给物品i打上了标签b的行为。
4.1 基于用户UGC标签进行推荐


4.1.1 最简单的算法（SimpleTagBased）

在拿到用户标签行为数据之后，一个最容易想到的方法就是：

    统计每个用户最常用的标签
    对于每个标签，统计被打过这个标签次数最多的物品
    对于每个用户，首先找到他常用的标签，然后找到具有这些标签的最热门物品进行推荐

用公式表示用户u对物品i的兴趣为，其中，nu,b
nu,b​是用户u打过标签b的次数，nb,i

nb,i​是物品i被打过标签b的次数。

p(u,i)=∑bnu,bnb,i

p(u,i)=b∑​nu,b​nb,i​
4.1.2 利用TF-IDF进行改进（TagBasedTFIDF和TagBasedTFIDF++）

上面的公式倾向于给热门标签对应的热门物品很大的权重，从而不能反映用户个性化的兴趣，因此可以借鉴TF-IDF思想，对上述公式进行改进（TagBasedTFIDF）：

p(u,i)=∑bnu,blog(1+n(u)b)nb,i

p(u,i)=b∑​log(1+nb(u)​)nu,b​​nb,i​

其中n(u)b

nb(u)​记录了标签b被多少个不同的用户使用过。

可见这个公式是对热门标签进行惩罚，当然对于热门物品也可以进行同样的惩罚（TagBasedTFIDF++）：

p(u,i)=∑bnu,blog(1+n(u)b)nb,ilog(1+n(u)i)

p(u,i)=b∑​log(1+nb(u)​)nu,b​​log(1+ni(u)​)nb,i​​

其中n(u)i

ni(u)​记录了物品i被多少个不同的用户打过标签
4.1.3 标签扩充改进

前面的算法中，用户兴趣和物品的联系是通过B(u)⋂B(i)

B(u)⋂B(i)中的标签建立的。但对于新用户或新物品，这个集合中的标签数量会很少，因此可以考虑对标签集合进行扩展。

一种简单的扩充方法是基于邻域的做法，即通过计算标签之间的相似度进行扩充。对于标签的相似度计算可以从数据中统计，当两个标签同时出现在很多物品的标签集合中时，就可以认为它们具有较大的相似度。

对于标签b，令N(b)
N(b)为有标签b的物品的集合，nb,i

nb,i​为给物品i打上标签b的用户数，可以用如下的余弦相似度计算标签b和标签b’的相似度：

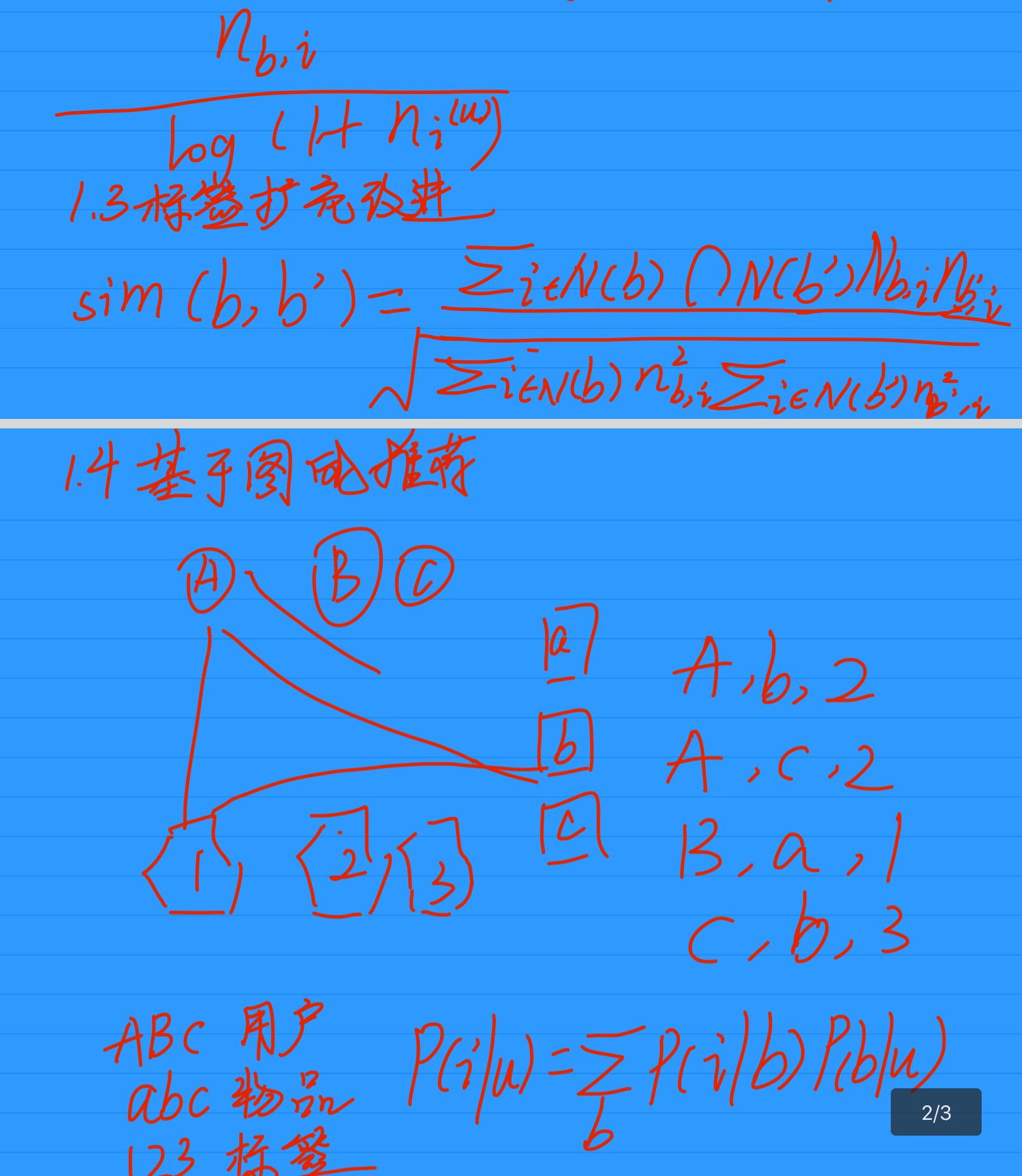
sim(b,b′)=∑i∈N(b)⋂N(b′)nb,inb′,i∑i∈N(b)n2b,i∑i∈N(b′)n2b′,i√
sim(b,b′)=∑i∈N(b)​nb,i2​∑i∈N(b′)​nb′,i2​

​∑i∈N(b)⋂N(b′)​nb,i​nb′,i​​

后续就可以根据这种标签的相似度进行聚合排序，而后作为用户新的标签集合。
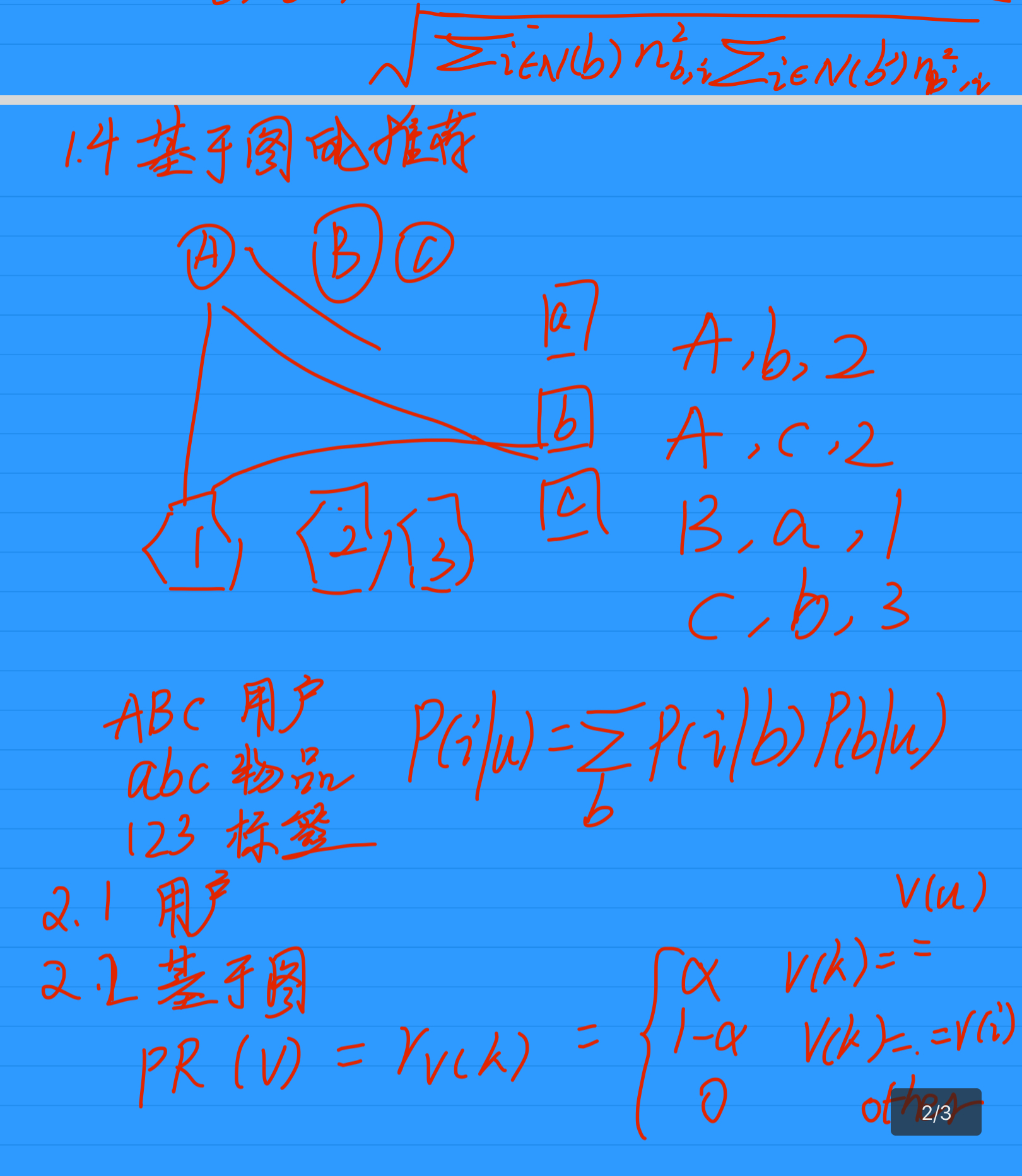
4.1.4 基于图的推荐

相比较于协同过滤算法中提到的(User, Item)二元组，这里的数据是(User, Item, Tag)三元组，因此也可以构建成如下的图：

其中ABC表示用户，abc表示物品，123表示标签。在建立了这种图之后，就可以用协同过滤部分提到的PersonalRank算法进行随机游走计算了。

而对于前面的简单算法来说，用户对物品的兴趣公式为：

P(i∣u)=∑bP(i∣b)P(b∣u)

P(i∣u)=b∑​P(i∣b)P(b∣u)

其实这个可以用简化的图模型来建模，即SimpleTagGraph，如下图所示，它将前面的三条边(User,Item)，(Item, Tag)，(User, Tag)改成了两条边，去掉了(User, Item)边，并且改为了有向图。

这时用PersonalRank算法， 设K=1

K=1，就等价于前面提到的简单推荐算法SimpleTagBased。
4.2 给用户推荐标签


给用户推荐标签的好处在于：1）方便用户输入；2）提升标签质量
4.2.1 基于统计的方法

当用户u给物品i打标签时，有如下4种方法给用户推荐和物品i相关的标签：

    PopularTags：给用户u推荐整个系统里面最热门的标签
    ItemPopularTags：给用户u推荐物品i上面被打的最热门标签
    UserPopularTags：给用户u推荐他自己经常打的标签
    HybridPopularTags：线性加权融合方式2、3，对两个列表进行线性相加之前，需要对其按照各自的最大值进行归一化

4.2.2 基于图的标签推荐

在根据用户打标签的行为生成图之后（4.1.4），同样可以利用PersonalRank方法进行排名。这次的问题是，当用户u遇到物品i时，会给物品i打什么样的标签。因此，需要重新定义顶点的启动概率：

PR⎛⎝⎜v⎞⎠⎟=rv(k)=⎧⎩⎨⎪⎪α1−α0v(k)==v(u)v(k)==v(i)other

PR(v)=rv(k)​=⎩⎨⎧​α1−α0​v(k)==v(u)v(k)==v(i)other​

也就是说，只有用户u和物品i对应的顶点有非0的启动概率，而其他顶点的启动概率都为0。在上面的定义中，v(u)
v(u)和v(i)v(i)的启动概率并不相同，v(u)v(u)的启动概率是αα，而v(i)v(i)的启动概率是1−α1−α。参数αα可以通过离线实验选择。