题目描述
在网友的国度中共有 nn 种不同面额的货币,第 ii 种货币的面额为 a[i]a[i],你可以假设每一种货币都有无穷多张。为了方便,我们把货币种数为 nn、面额数组为 a[1..n]a[1..n] 的货币系统记作 (n,a)(n,a)。
在一个完善的货币系统中,每一个非负整数的金额 xx 都应该可以被表示出,即对每一个非负整数 xx,都存在 nn 个非负整数 t[i]t[i] 满足 a[i] imes t[i]a[i]×t[i] 的和为 xx。然而, 在网友的国度中,货币系统可能是不完善的,即可能存在金额 xx 不能被该货币系统表示出。例如在货币系统 n=3n=3, a=[2,5,9]a=[2,5,9] 中,金额 1,31,3 就无法被表示出来。
两个货币系统 (n,a)(n,a) 和 (m,b)(m,b) 是等价的,当且仅当对于任意非负整数 xx,它要么均可以被两个货币系统表出,要么不能被其中任何一个表出。
现在网友们打算简化一下货币系统。他们希望找到一个货币系统 (m,b)(m,b),满足 (m,b)(m,b) 与原来的货币系统 (n,a)(n,a) 等价,且 mm 尽可能的小。他们希望你来协助完成这个艰巨的任务:找到最小的 mm。
输入格式
输入文件的第一行包含一个整数 TT,表示数据的组数。
接下来按照如下格式分别给出 TT 组数据。 每组数据的第一行包含一个正整数 nn。接下来一行包含 nn 个由空格隔开的正整数 a[i]a[i]。
输出格式
输出文件共有 TT 行,对于每组数据,输出一行一个正整数,表示所有与 (n,a)(n,a) 等价的货币系统 (m,b)(m,b)中,最小的 mm。
输入输出样例
2 4 3 19 10 6 5 11 29 13 19 17
2 5
说明/提示
在第一组数据中,货币系统 (2, [3,10])(2,[3,10]) 和给出的货币系统 (n, a)(n,a) 等价,并可以验证不存在 m < 2m<2 的等价的货币系统,因此答案为 22。 在第二组数据中,可以验证不存在 m < nm<n 的等价的货币系统,因此答案为 55。
【数据范围与约定】
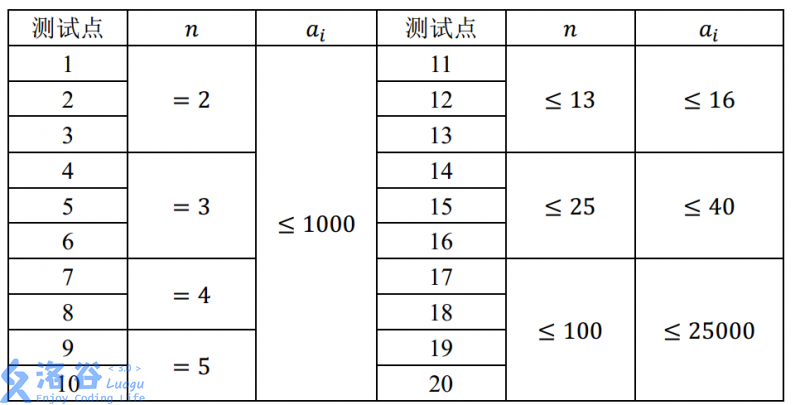
对于 100\%100% 的数据,满足 1 ≤ T ≤ 20, n,a[i] ≥ 11≤T≤20,n,a[i]≥1。
一波玄学DFS,说好的88变成了60.。。。。。
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; int t,ans,f=0; int a[105],b[10000005]; inline int read() { int x=0; char ch=getchar(); char c=ch; while(ch>'9'||ch<'0')c=ch,ch=getchar(); while(ch<='9'&&ch>= '0')x=x*10+ch-'0',ch=getchar(); if(c=='-')x=x*-1; return x; } void dfs(int x,int y){ int j; if(x<0){ return; } if(x==0){ if(b[f]==a[y]){ return; } else{ f++; b[f]=a[y]; return; } } for(j=1;j<y;j++){ dfs(x-a[j],y); } } int main(){ t=read(); while(t--){ int n,i; scanf("%d",&n); for(i=1;i<=n;i++){ a[i]=read(); } sort(a+1,a+1+n); ans=n; for(i=2;i<=n;i++){ dfs(a[i],i); } int anb=0; for(i=1;i<=f;i++){ if(b[i]!=b[i-1]){ anb++; } } ans-=anb; printf("%d ",ans); memset(b,0,f+1); f=0; } return 0; }